ÉLECTROCINÉTIQUE - RÉSEAUX - corrigé des exercices

A.EXERCICES DE BASE

I. Théorème de superposition et “grillage infini”

1.	• Chaque branche du grillage a une caractéristique affine (simple résistance), donc le système d'équations décrivant le réseau est linéaire et on peut utiliser le théorème de superposition.

• Pour que la superposition soit correcte, il faut en particulier qu'elle respecte la superposition des courants imposés par les générateurs :

◊	le courant qui entre dans le grillage en $A$ est $I_c$ dans le schéma de gauche et nul dans le schéma de droite, cela donne bien un total $I_c$ comme dans le réseau réel ;
◊	le courant qui sort du grillage en $B$ est nul dans le schéma de gauche et $I_c$ dans le schéma de droite, cela donne bien un total $I_c$ comme dans le réseau réel ;
◊	le courant qui sort du grillage à l'infini est $I_c$ dans le schéma de gauche et $-I_c$ dans le schéma de droite, cela donne bien un total nul comme dans le réseau réel.

• Le fil “à l'infini”, “infiniment long” et de résistance nulle, est physiquement irréalisable. Mais les deux schémas qu'on superpose ne sont que des représentations symboliques de ce que serait le système physique décrit par les équations mathématiques intervenant dans les calculs intermédiaires. Le fait qu'un tel système physique ne puisse pas exister importe peu si le système d'équations mathématiques se simplifie à la fin et que la solution mathématique décrit finalement correctement un système physique réel.
◊ remarque : un supplément est proposé en annexe.

• Si la périphérie du grillage est supposée infiniment conductrice, le point de branchement à l'infini peut être placé de n'importe quel côté. Le schéma de gauche est alors invariant par symétrie selon un axe vertical passant par

A

, donc le courant dans la branche à droite de

A

est égal au courant dans la branche à gauche de

A

.
• En considérant de même les symétries par rapport à un axe horizontal, puis par rapport à des axes inclinés selon les diagonales, on conclut que les courants dans les quatre branches issues de

A

sont égaux entre eux, donc sont égaux à

\frac{I_c}{4}

5.	• On peut en déduire dans le schéma de gauche : $U_{AB}=r \:\frac{I_c}{4}$ . • De même, le schéma de droite correspond à un courant $\frac{I_c}{4}$ dans chacune des quatre branches qui se rejoignent en $B$ . Ceci correspond de même à : $U_{AB}=r \:\frac{I_c}{4}$ .

6.	• Par superposition de ces deux contributions, le courant dans la branche $AB$ est $\frac{I_c}{2}$ et la tension correspondante est : $U_{AB}=r \:\frac{I_c}{2}$ , c’est-à-dire que la résistance équivalente est : $R=\frac{r}{2}$ .

◊ supplément à la question 3.
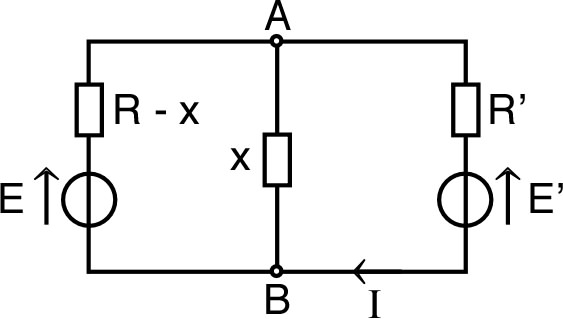
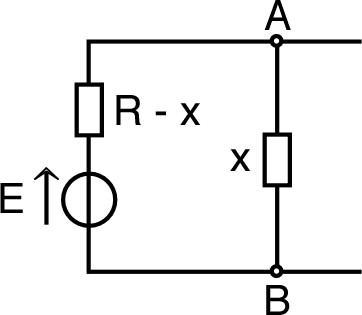
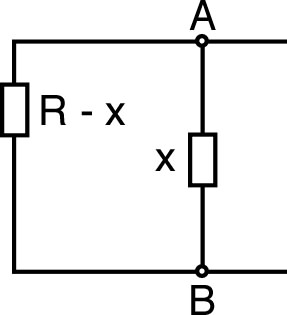
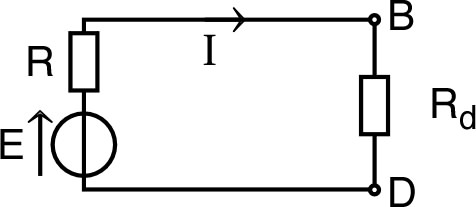
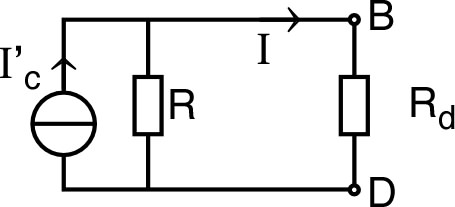
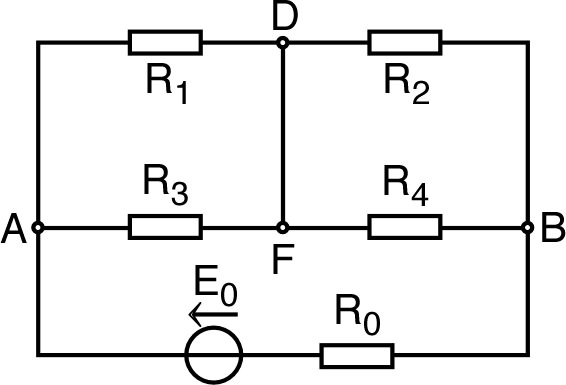
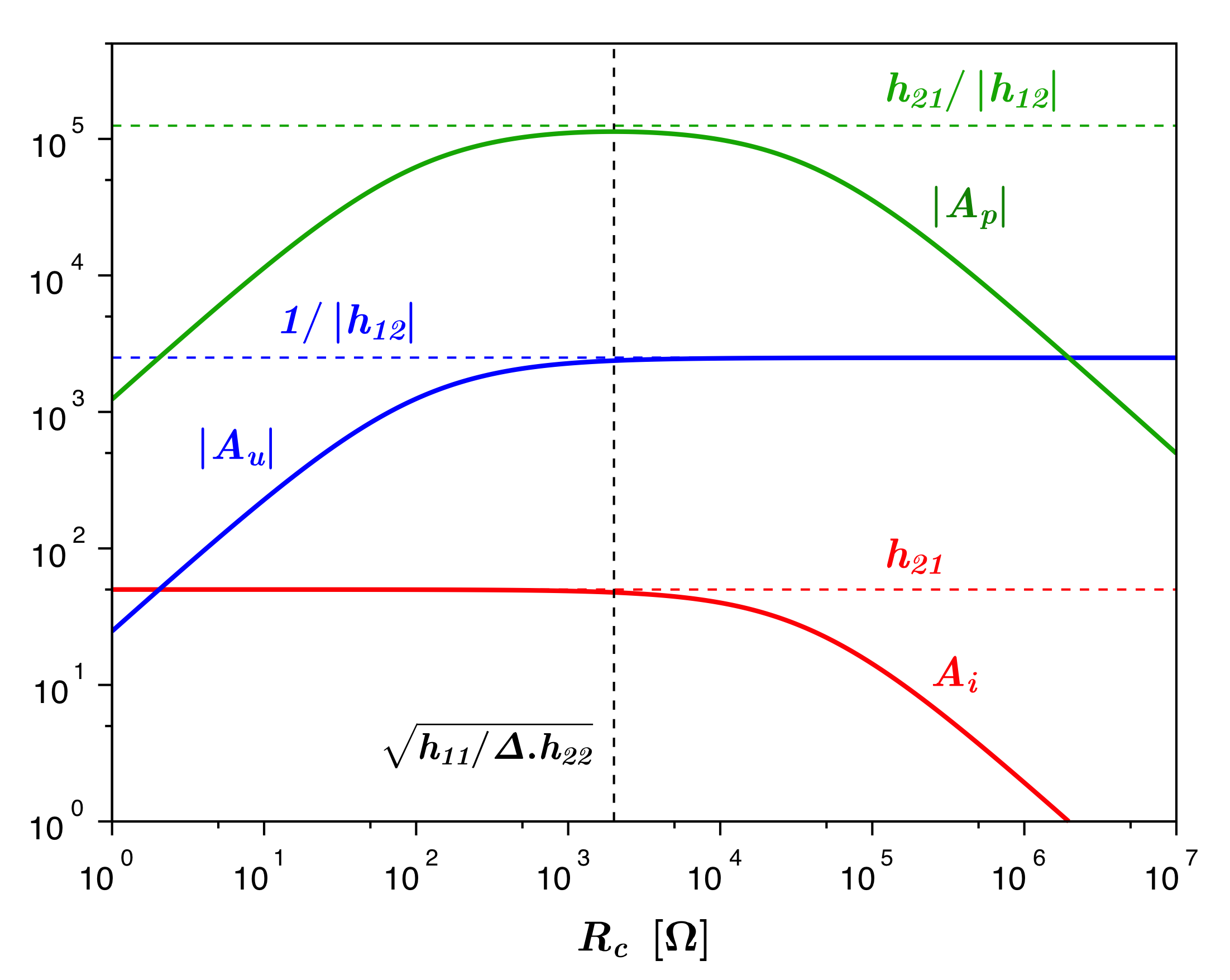
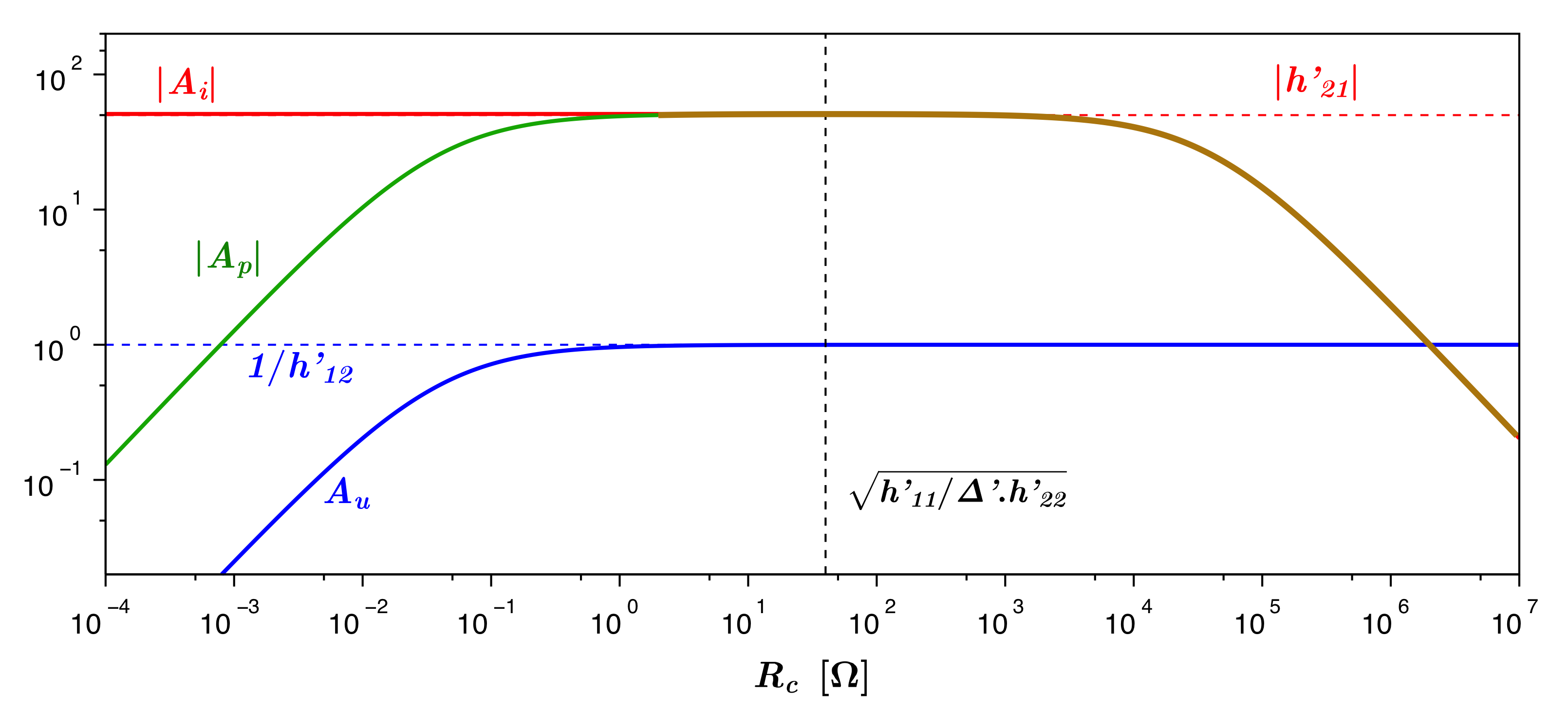
• On peut douter de l'utilisation du fil conducteur idéal à l'infini ; il peut alors être intéressant de vérifier la validité du raisonnement par une autre approche : une suite de circuits finis de taille croissante, avec à chaque étape un intervalle de valeurs pour la résistance estimée. Un intérêt essentiel de cet approfondissement est de mettre en évidence le rôle important des symétries.
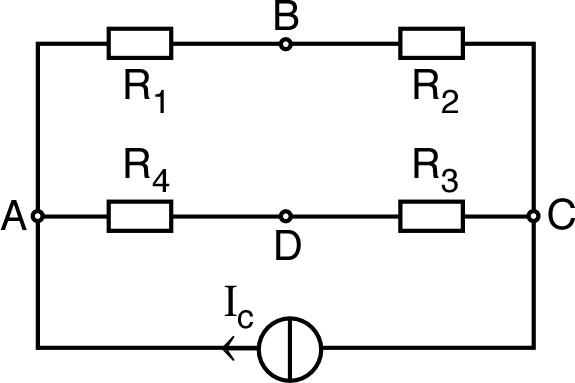
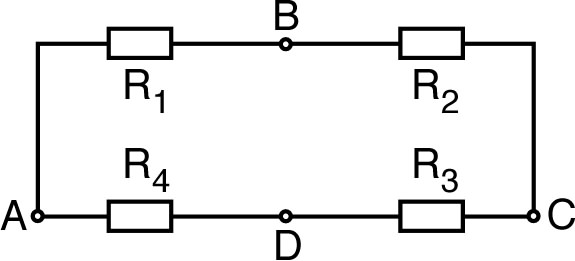
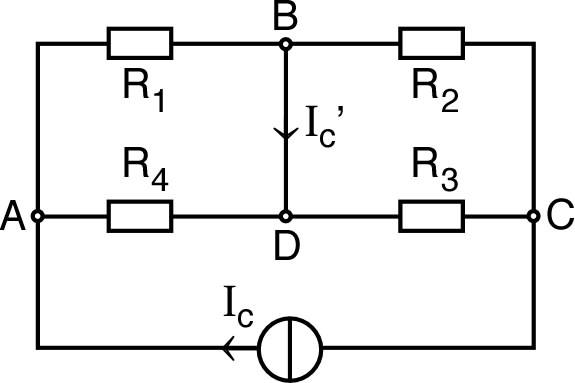
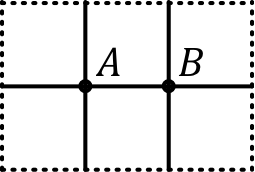
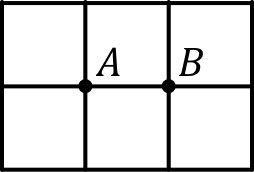
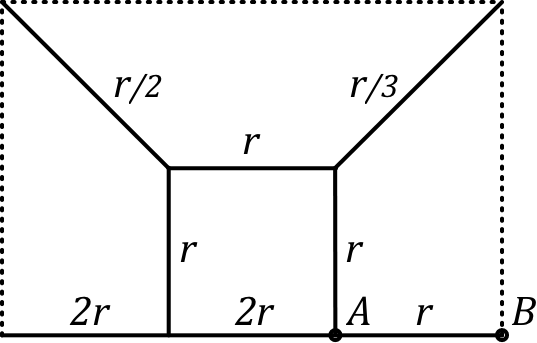
• Considérons donc un tel réseau “minimal” entourant

A

B

avec six mailles, dont deux variantes donnent un encadrement de la résistance cherchée :

◊	celui de gauche (avec en pointillés un conducteur idéal) sous-estime la résistance puisqu'il court-circuite une partie des conducteurs ;
◊	celui de droite sur-estime au contraire puisqu'il omet d'autres conducteurs qui seraient autour et amélioreraient la conductance.

• Le schéma de gauche peut être nettement simplifié puisque de chaque côté les trois résistances sont ainsi en parallèle ; on aboutit alors à :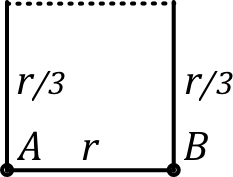

R>\frac{2}{5} \,r=0,4 \;r

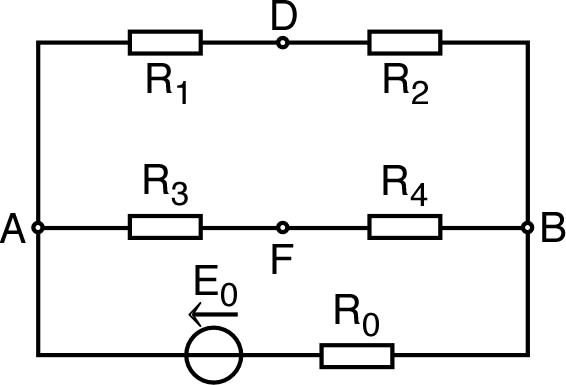
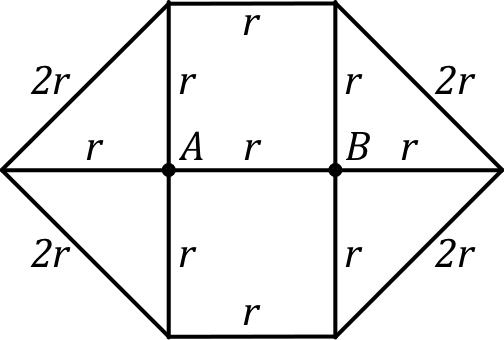
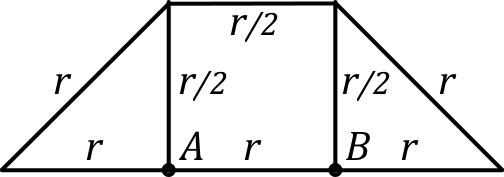
• Le schéma de droite peut aussi être simplifié, en particulier avec la symétrie d'axe

AB

; on aboutit ainsi à :

R<\frac{13}{23} \,r≈0,565 \;r

. L'intervalle est grand (

≈±20 \:%

), mais l'intérêt est d'étudier la suite.

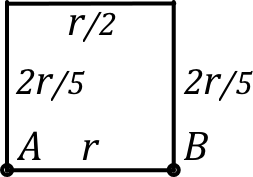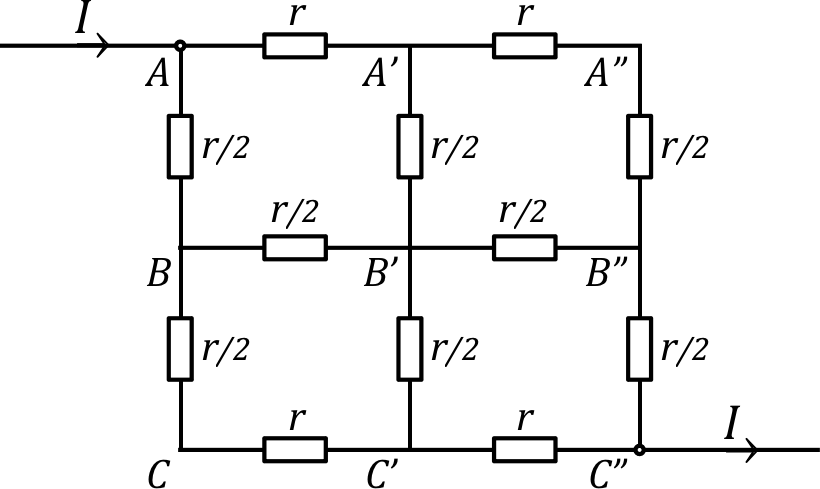
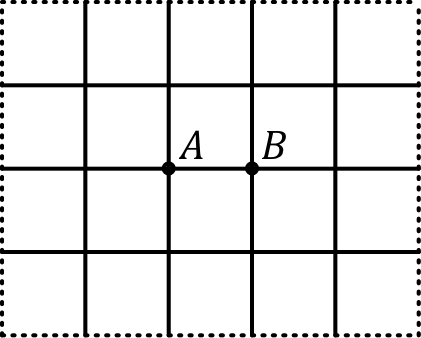
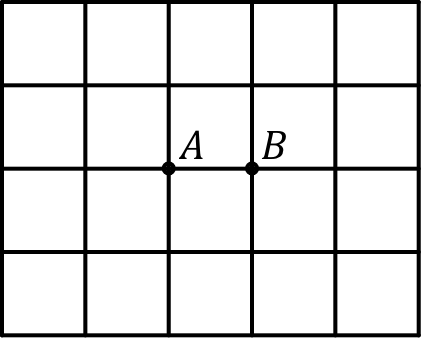
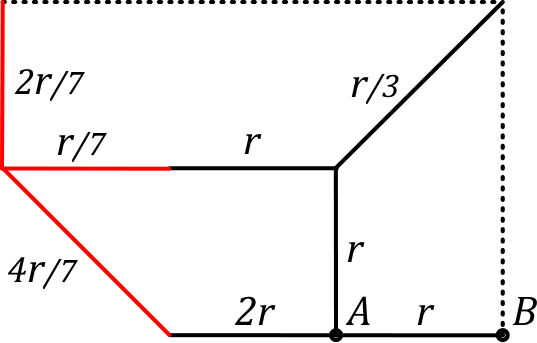
• À l'ordre suivant, on considère de même deux réseaux de 14 mailles :

• Le schéma de gauche peut être simplifié par symétrie d'axe

AB

, mais en outre on peut appliquer la tension

U=U_{AB}

de façon symétrique en plaçant la masse du circuit au milieu de

AB

V_A=\frac{U}{2}

V_B=-\frac{U}{2}

. Par symétrie tous les points de l'axe vertical passant par la masse sont au même potentiel nul, donc on peut raisonner comme s'ils étaient court-circuités (les potentiels sont inchangés, donc les courants de même).

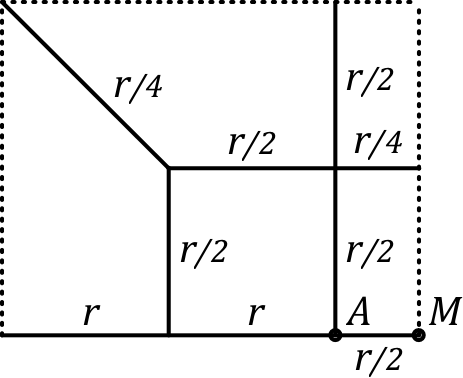• Pour le réseau moitié, la résistance entre

A

M

est alors moitié de celle cherchée ; pour retrouver un réseau équivalent, il suffit de doubler toutes les résistances et donc la tension (pour les mêmes courants), ce qui correspond à

U_{AM}=U

(dans la suite on peut renommer

B

le point

M

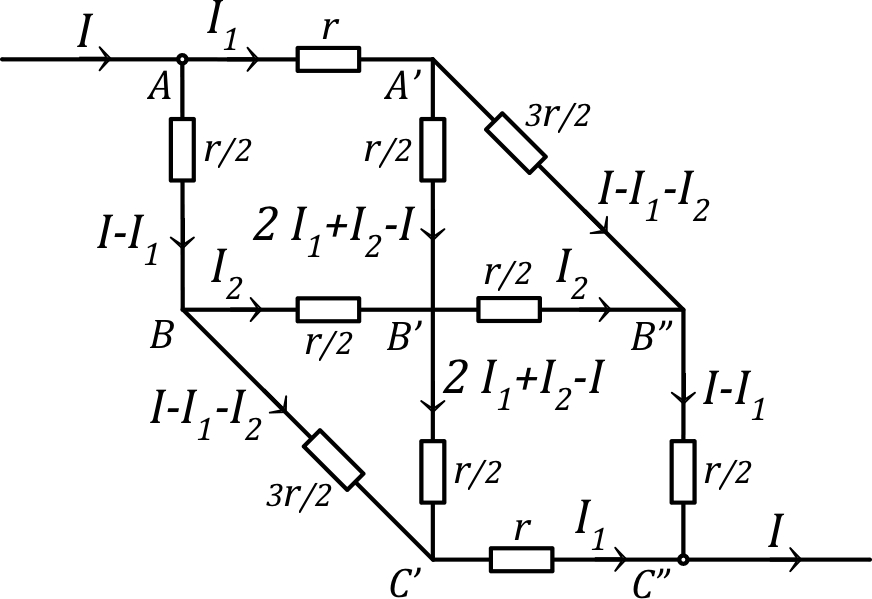
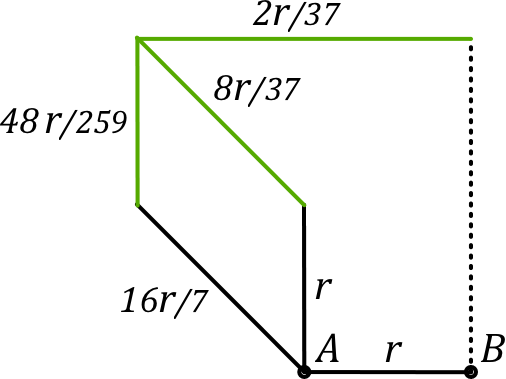
• La maille en triangle (vu le court-circuit) à gauche peut être changée en étoile, puis de même celle du haut... les simplifications parallèle-série donnent finalement :

R>\frac{44}{93} \,r≈0,473 \;r

.
◊ remarque : on pourrait aussi se ramener à 4 loi des mailles entre 4 courants (indépendants).
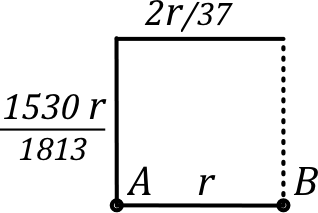
• La même méthode appliquée au réseau non court-circuité donne :

R<\frac{2391}{4579} \,r≈0,522 \;r

.
◊ remarque : c'est encore faisable “à la main”, mais à la fin les coefficients se compliquent ; il peut être prudent de vérifier avec un logiciel de calcul formel.
• On vérifie ainsi que la borne inférieure augmente et que celle supérieure diminue ; sans être extrêmement rapide, la convergence est nette (écart

≈± 5 \:%

) ; l'influence du court circuit devient d'autant plus négligeable que le réseau est grand. Pour un réseau “infini” (très, très grand) on peut raisonner avec un court-circuit théorique ; cela ne modifie pas l'expression limite et permet d'exploiter très efficacement les symétries globales pour trouver le résultat très rapidement.

II. Électrolyseur

• L'énoncé indique

E>0

donc le schéma du générateur correspond à la convention de signe “usuelle”. Puisque l'électrolyseur est un dipôle passif, le générateur impose dans les branches de droite un courant du haut vers le bas, ce qui correspond à

I≥0

.
◊ remarque : le courant peut être nul si la tension imposée entre ses bornes est insuffisante pour provoquer l'électrolyse.

2.	• Avec les notations de Thévenin, on peut utiliser le schéma équivalent suivant (où on a aussi schématisé le montage du rhéostat) :

• On peut séparer le problème en deux parties : remplacer l'assemblage de gauche (générateur parfait plus montage “diviseur de tension”) par un générateur équivalent, réglable en tension, puis étudier le courant imposé par ce générateur selon la loi de Pouillet.

• La force électromotrice

E''

du générateur de Thévenin équivalent est la tension “à vide”, c'est-à-dire pour

I=0

. On obtient dans ce cas (diviseur de tension) :

E =U_{{AB}_{(0)}}=E \:\frac{x}{R}

.
• La résistance

R''

du générateur équivalent est celle qu'on obtient en considérant le générateur à l'arrêt, c'est-à-dire pour

E=0

. Ceci correspond à deux résistances

x

R-x

en parallèle, donc :

R''=\frac{x.(R-x)}{R}

.
• En cours d'électrolyse, on obtient donc (tant que cette relation correspond à une valeur positive) :

I=\frac{E''-E'}{R''+R'}=\frac{x \,E-R \,E'}{R \,R'+x.(R-x)}

.
• La relation précédente est ainsi valable pour

x≥x_0=\frac{R \,E'}{E}=4 \:\mathrm{Ω}

; par contre pour

0<x<x_0

on obtient

I=0

.
• Ceci donne finalement le graphique suivant :

III. Pont de Wheatstone et source de courant

• Pour utiliser la représentation de Thévenin, on modélise la partie du réseau complémentaire de

R_d

par un générateur de Thévenin de force électromotrice

E

et de résistance

R

• La f.e.m.

E

est égale à la tension

U_{BD}

“à vide” (sans

R_d

). La méthode du diviseur de courant donne :

I_1=I_c \,\frac{R_3+R_4}{R_1+R_2+R_3+R_4}

I_4=I_c \,\frac{R_1+R_2}{R_1+R_2+R_3+R_4}

, puis :

E=U_{{BD}_{(0)}}=R_4 \,I_4-R_1 \, I_1=I_c \,\frac{R_2 R_4-R_1 R_3}{R_1+R_2+R_3+R_4}

• La résistance

R

est égale à la résistance du même circuit, avec générateur à l'arrêt (

I_c=0

, ce qui correspond à “ouvrir” cette branche du circuit). Or, cette résistance correspond à

R_1+R_4

en parallèle avec

R_2+R_3

R= \frac{(R_1+R_4 )(R_2+R_3 )}{R_1+R_2+R_3+R_4}

• Pour le montage simplifié, la loi de Pouillet donne :

I=\frac{E}{R+R_d}=I_c \,\frac{R_2 R_4-R_1 R_3}{(R_1+R_4 )(R_2+R_3 )+R_d.(R_1+R_2+R_3+R_4 )}

• Pour utiliser la représentation de Norton, on modélise la partie du réseau complémentaire de

R_d

par un générateur de Norton de courant de court-circuit

I_c'

et de résistance

R

• D'après la question précédente, par équivalence Thévenin/Norton, on sait que le courant de court-circuit est :

I_c'=\frac{E}{R}=I_c \:\frac{R_2 \,R_4-R_1 \,R_3}{(R_1+R_4 )(R_2+R_3 )}

; mais on peut le calculer en court-circuitant

B

D

. La méthode du diviseur de courant donne :

I_1=I_c \:\frac{R_4}{R_1+R_4}

I_2=I_c \:\frac{R_3}{R_2+R_3}

, d’où

I_c'=I_1-I_2 = I_c \:\frac{R_2 R_4-R_1 R_3}{(R_1+R_4 )(R_2+R_3 )}

.
• Le calcul de la résistance

R

est le même que précédemment :

R= \frac{(R_1+R_4 )(R_2+R_3 )}{R_1+R_2+R_3+R_4}

. Pour le montage simplifié, la méthode du diviseur de courant donne :

I=I_c' \:\frac{R}{R+R_d} =I_c \:\frac{R_2 \,R_4-R_1 \,R_3}{(R_1+R_4 )(R_2+R_3 )+R_d.(R_1+R_2+R_3+R_4 )}

B. EXERCICES D’APPROFONDISSEMENT

IV. Association de résistances

1.	• Les couples de points symétriques $(B,\,D)$ , $(B',\,D')$ et $(B'',\,D'')$ sont reliés de façon symétrique, donc le réseau est globalement symétrique par rapport au plan considéré.

2.	• Les points symétriques considérés sont aux mêmes potentiels ; on peut les court-circuiter sans modifier la répartition des courants.

• En “aplatissant” le réseau “diagonalement” (

D

D'

D''

sont respectivement confondus avec

B

B'

B''

) et en remplaçant chaque paire de résistances

r

en parallèle par une résistance

\frac{r}{2}

, on obtient le réseau équivalent suivant, qui peut encore se simplifier par des associations en série :

• Dans un tel réseau, on peut continuer à simplifier par des équivalences triangle-étoile (triangles

A'B'B''

BB'C'

) ; mais compte tenu de la symétrie centrale il n'y a que deux mailles élémentaires indépendantes, donc en utilisant la loi des nœuds, on peut facilement limiter à deux courants inconnus.
• En écrivant la loi des mailles, par exemple pour les deux mailles de gauche, on obtient :

r \:I_1+\frac{r}{2} \,(2 \,I_1+I_2-I)-\frac{r}{2} \,I_2-\frac{r}{2} \,(I-I_1 )=0

;

\frac{r}{2}\,I_2+\frac{r}{2}\,(2 \,I_1+I_2-I)-\frac{3 \,r}{2} \,(I-I_1-I_2 )=0

• De la première équation, on déduit :

I_1=\frac{2}{5} \,I

; en reportant dans la seconde, on obtient :

I_2=\frac{2}{5}\,I

.
• Ainsi :

U_{AB}=r \,I_1+\frac{3 \,r}{2} \,(I-I_1-I_2 )+\frac{r}{2} \,(I-I_1 )=r \:I

, d'où la résistance équivalente :

R=r

V. Pont de Wheatstone

• On considère le circuit “à vide” ci-contre.

La f.é.m. (tension

U_{DF}

“à vide”, en l'absence de

R_5

) peut se calculer à partir de la loi de Millman et de la méthode du pont diviseur de tension :

U_{AB}=\frac{G_0 \,E_0}{G_0+G_{12}+G_{34}}

avec

G_{12}=\frac{1}{R_1+R_2}

G_{34}=\frac{1}{R_3+R_4}

;

U_{AD}=U_{AB} \,\frac{R_1}{R_1+R_2}=U_{AB} \,R_1 \,G_{12}

U_{AF}=U_{AB} \,R_3 \,G_{34}

;

E=U_{DF}=U_{AF}-U_{AD}=\frac{G_0 E_0}{G_0+G_12+G_34} \:[R_3 \,G_{34} - R_1\, G_{12} ]=\frac{G_0 E_0}{G_0+G_12+G_34} \:\frac{R_2 \,R_3-R_1 \,R_4}{(R_1+R_2 )(R_3+R_4 )}

• L’équilibre du pont, défini par l’une ou l’autre des conditions :

I_5=\frac{E}{R+R_5}=0

U_{DF}=R_5 \,I_5=0

, correspond à :

E=0

, c’est-à-dire :

R_1\,R_4=R_2 \,R_3

VI. Pont de Wheatstone

• On considère le circuit “à vide” ci-contre.

Le courant de court circuit (courant

I_{DF}

“à vide”, en l'absence de

R_5

) peut se calculer à partir de la loi de Pouillet et de la méthode du pont diviseur de courant :

I_0=\frac{E_0}{R_0+R_{13}+R_{24}}

avec

R_{13}=\frac{1}{G_1+G_3}

R_{24}=\frac{1}{G_2+G_4}

;

I_1=I_0 \,\frac{G_1}{G_1+G_3}=I_0 \,G_1 \,R_{13}

I_2=I_0 \,G_2 \,R_{24}

;

I_c=I_{DF}=I_1-I_2=\frac{E_0}{R_0+R_{13}+R_{24}} \:[G_1 \,R_{13} - G_2 \,R_{24} ]=\frac{E_0}{R_0+R_{13}+R_{24}} \:\frac{R_2 \,R_3-R_1 \,R_4}{(R_1+R_3 )(R_2+R_4 )}

• L’équilibre du pont, défini par l’une ou l’autre des conditions :

U_{DF}=\frac{I_c}{G+G_5}=0

I_5=G_5 \,U_{DF}=0

, correspond à :

I_c=0

, c’est-à-dire :

R_1 \,R_4=R_2 \,R_3

.
◊ remarque : on peut "mélanger" les notations de Thévenin et de Norton.

VII. Étude d'un transistor

1.	• D’après le modèle équivalent : $U_1 (I_1,\,U_2 )=h_{11} \,I_1+h_{12} \,U_2$ . Par ailleurs, le courant dans le résistor de conductance $h_{22}$ est : $h_{22} \,U_2=I_2-h_{21} \,I_1$ ; donc inversement : $I_2 (I_1 \,,U_2 )=h_{22} \,U_2+h_{21} \,I_1$ .

2.a.

• Pour une sortie sur une résistance

R_c

on obtient :

U_2=-R_c \,I_2

et donc :

I_2=-h_{22} \,R_c \,I_2+h_{21} \,I_1

. On en déduit :

A_i=\frac{I_2}{I_1} =\frac{h_{21}}{1+h_{22} \,R_c}

2.b.

• D’après ce qui précède, on obtient :

I_1=\frac{I_2}{A_i} =-\frac{U_2}{R_c \,A_i}

donc :

U_1=-h_{11} \,\frac{U_2}{R_c \,A_i}+h_{12} \,U_2

. On en déduit :

A_u=\frac{U_2}{U_1} =-\frac{R_c \,h_{21}}{h_{11}+Δ .R_c}

2.c.

• On obtient ainsi :

A_p=\frac{U_2 \,I_2}{U_1 \,I_1}=A_u \,A_i=-\frac{R_c \,h_{21}^{\; 2}}{(h_{11}+Δ .R_c )(1+h_{22} \,R_c )}

2.d.

• Le gain “maximum” (en valeur absolue) correspond à

\frac{∂\left|A_p \right|}{∂R_c}=0

c’est-à-dire à :

Δ .h_{22} \:R_c^{\:2}-h_{11}=0

et donc :

R_c=\sqrt{\frac{h_{11}}{Δ .h_{22}}}≈2000 \:\mathrm{Ω}

2.e.

• Pour cette valeur particulière de

R_c

on obtient :

A_i≈48≈h_{21}=50

;

\left|A_u \right|≈2400≈\frac{1}{\left|h_{12}\right|} =2500

;

\left|A_p \right|≈115000≈\frac{h_{21}}{\left|h_{12}\right|} =125000

• L'allure de la variation des gains est la suivante :

◊ remarque : les gains

A_u

A_p

sont négatifs donc on raisonne sur leur valeur absolue ; par ailleurs, les importantes variations des gains sont mieux représentées en échelles logarithmiques.

3.a.	• Pour le montage “collecteur commun” : $I'_1=I_1$ ; $I'_2=-I_1-I_2$ ; $U'_1=U_1-U_2$ ; $U'_2=-U_2$ .

3.b.	• On peut écrire : $U'_1=(h_{11} \,I_1+h_{12} \,U_2 )-U_2$ ; donc $U'_1=h'_{11} \:I'_1+h'_{12} \:U'_2$ avec $h'_{11}=h_{11}=2 \:\mathrm{Ω}$ et $h'_{12}=1-h_{12}=1,0004≈1$ . • De même : $I'_2=-I_1-(h_{22} \,U_2+h_{21} \,I_1 )$ ; donc $I'_2=h'_{21} \:I'_1+h'_{22} \:U'_2$ avec $h'_{21}=-1-h_{21}=-51$ et $h'_{22}=h_{22}=25 \:\mathrm{μS}$ . ◊ remarque : cela donne $Δ'=h'_{11} \:h'_{22}-h'_{12} \:h'_{21}=Δ+1-h_{12}+h_{21}≈51$ (alors que $Δ≈2.{10}^{-2}$ ).

3.c.	• Pour ce montage le maximum correspond à : $R_c=\sqrt{\frac{h'_{11}}{Δ'.\,h'_{22}}}≈40 \:\mathrm{Ω}$ ; pour cette valeur on obtient : $\left\|A_i \right\|≈51≈\left\|h'_{21}\right\|$ ; $A_u≈1≈\frac{1}{h'_{12}}$ ; $\left\|A_p \right\|≈51≈\frac{\left\|h'_{21}\right\|}{h'_{12}}$ . ◊ remarque : pourvu que le courant demandé ne soit pas trop grand ( $R_c$ pas trop petit), ce montage est “suiveur de tension” avec amplification du courant. • On obtient pour ce montage les variations suivantes :