ÉLECTROCINÉTIQUE - RÉSEAUX

ÉLECTROCINÉTIQUE - RÉSEAUX - exercices

A. EXERCICES DE BASE

I. Théorème de superposition et “grillage infini”

• On considère un “grillage infini” dont chaque branche a une même résistance

r

et qui est alimenté entre deux nœuds voisins (

A

B

) par un générateur de courant.

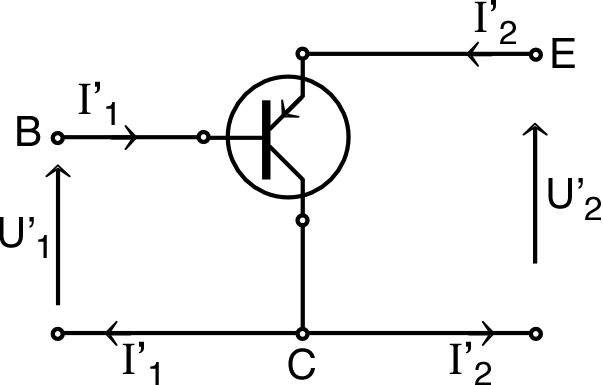
1. • Justifier qu'on peut utiliser avec ce réseau le théorème de superposition.

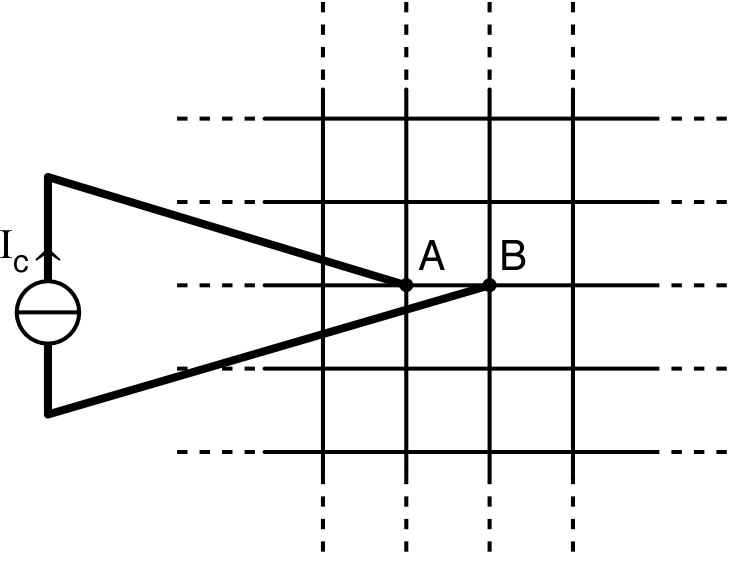
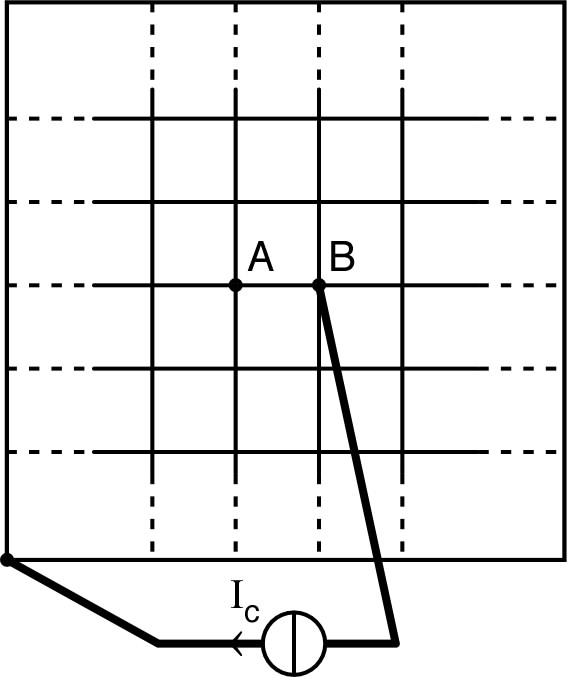
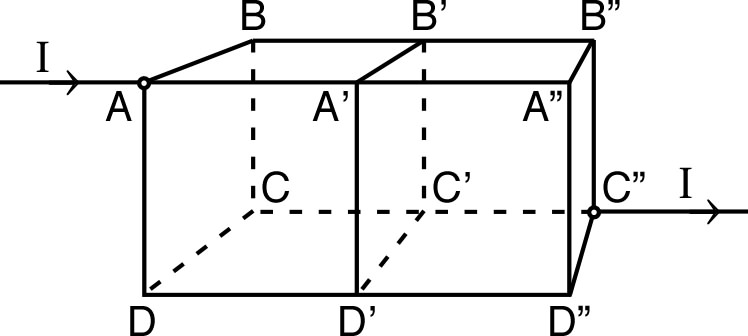
2. • On envisage d'utiliser le théorème de superposition avec les schémas ci-dessous, où le réseau est un peu modifié : la périphérie du grillage, “infiniment” éloignée, est supposée court-circuitée par un fil infiniment conducteur. Justifier que la superposition des courants des deux schémas est bien compatible avec le montage du réseau réel.

3. • Justifier que, bien que physiquement impossible, la modification “théorique” du réseau ne change pas la conclusion finale du raisonnement.

4. • En considérant les symétries du réseau, dans le schéma de gauche, déterminer la répartition du courant

I_c

dans les quatre fils du grillage reliés en

A

.

5. • En déduire la relation entre

U_{AB}

I_c

dans ce réseau ; puis de même dans le réseau de droite.

6. • Exprimer la relation dans le réseau réel, puis en déduire la résistance équivalente cherchée.

II. Électrolyseur

• On considère un électrolyseur (dont la caractéristique est rappelée ci-après) branché en sortie d'un montage “réducteur de tension”, avec un générateur de f.e.m.

E=10 \:\mathrm{V}

et de résistance interne négligeable, associé à un rhéostat de résistance

R=10 \:\mathrm{Ω}

(au total). On note

x

la résistance de la partie “inférieure” du rhéostat (et donc

R-x

la résistance de la partie “supérieure”).
◊ remarque : l'expression “diviseur de tension” serait ici un abus de langage, dans la mesure où le passage du courant

I

dans l'électrolyseur fait que ce n'est pas forcément le même courant dans

x

R-x

1. • La convention de sens de mesure du courant

I

est-elle arbitraire ou correspond-elle au sens réel ?

2. • En cours d'électrolyse, l'électrolyseur a une f.c.e.m.

E'=4 \:\mathrm{V}

et une résistance

R'=2 \:\mathrm{Ω}

. Dessiner un schéma équivalent avec les notations de Thévenin.

3. • En utilisant la méthode de Thévenin ou de Norton, calculer, en fonction de

x∈[0 \,; R]

, le courant

I

dans l'électrolyseur, puis tracer la courbe représentative de

I(x)

III. Pont de Wheatstone et source de courant

• On considère le “pont de Wheatstone” ci-contre, alimenté par un générateur de courant.

1. • Calculer, par le théorème de Thévenin, le courant

I

dans

R_d

.

2. • Calculer, par le théorème de Norton, le courant

I

dans

R_d

B. EXERCICES D’APPROFONDISSEMENT

IV. Association de résistances

• On considère le double-cube suivant, dont les vingt arêtes sont constituées de fils identiques de résistance

r

1. • Ce double-cube est relié à un circuit extérieur par deux sommets opposés

A

C''

. Montrer que ce réseau est symétrique par rapport au plan

AA''C''C

.

2. • Justifier qu'on obtient un réseau équivalent en court-circuitant respectivement :

B

D

;

B'

D'

;

B''

D''

.

3. • Simplifier le réseau ainsi obtenu à l'aide des quelques équivalences “série” et “parallèle” mises alors en évidence (il est plus simple de raisonner sur un dessin en projection “à plat” sur le plan

AA''C''C

).

4. • Établir la relation entre la tension

U_{AC''}

et le courant

I

, puis en déduire la résistance équivalente de l'ensemble (on peut encore utiliser les symétries pour préciser la répartition des courants).

V. Pont de Wheatstone

• Établir la condition d'équilibre du pont de Wheatstone suivant, par la méthode de Thévenin, en considérant la f.e.m. équivalente de l'ensemble du montage privé de la branche

DF

VI. Pont de Wheatstone

• Établir la condition d'équilibre du pont de Wheatstone suivant, par la méthode de Norton, en considérant le courant de court circuit équivalent de l'ensemble du montage privé de la branche

DF

VII. Étude d'un transistor

• Un transistor est un tripôle, utilisé en quadripôle en branchant une des bornes en commun entre l'entrée et la sortie. Les trois bornes sont notées

E

(émetteur),

B

(base) et

C

(collecteur).

1. • On considère le montage “émetteur commun” (ici pour un transistor PNP) et un modèle symbolique équivalent (on raisonne uniquement sur le schéma équivalent) :

◊ remarque : la conservation de l'énergie nécessite, en plus de la source de tension qui fournit

U_1

, une alimentation dans le circuit de sortie (non représentée ici).

• Exprimer

U_1 (I_1\,,\,U_2 )

I_2 (I_1\,,\,U_2 )

à l'aide des coefficients

h_{ij}

(“paramètres hybrides”).

2. • Le montage, soumis en entrée à la tension

U_1

, débite en sortie le courant

I_2

dans une résistance de charge

R_c

(branchée entre

C

E

).
a) Calculer le gain en courant :

A_i=\frac{I_2}{I_1}

en fonction des

h_{ij}

, de

R_c

et de

Δ=h_11 \,h_22-h_12 \,h_21

.
b) Calculer de même le gain en tension :

A_u=\frac{U_2}{U_1}

.
c) Calculer de même le gain en puissance :

A_p=\frac{U_2 \,I_2}{U_1 \,I_1}

.
d) Pour quelle valeur de

R_c

le gain en puissance

A_p

est-il maximal ?
e) Dans le cas :

h_{11}=2 \:\mathrm{Ω}

;

h_{12}=-4.{10}^{-4}

;

h_{21}=50

;

\frac{1}{h_{22}} =40 \:\mathrm{kΩ}

; représenter l'allure des variations de

A_i

A_u

A_p

en fonction de

R_c

; calculer en particulier ces gains pour la valeur de

R_c

qui rend

A_p

maximal.

3. • On considère maintenant le montage “collecteur commun” (la résistance de charge est branchée entre

E

C

).
a) Relier les grandeurs

I'_1

I'_2

U'_1

U'_2

à celles du premier montage (

I_1

I_2

U_1

U_2

).
b) Montrer que (exprimer les

h'_{ij}

en fonction des

h_{ij}

) :

U'_1=h'_{11} \:I'_1+h'_{12} \:U'_2

;

I'_2=h'_{21} \:I'_1+h'_{22} \:U'_2

.
c) Reprendre les applications numériques de la question (2) pour ce montage.