RÉGIME SINUSOÏDAL ; IMPÉDANCES

RÉGIME SINUSOÏDAL ; IMPÉDANCES - TP1

1. Principe

• Les circuits étudiés comportent des résistors, des condensateurs et des bobines à inductance ; on utilise des cas particuliers de la relation donnant l’impédance

Z

d’un circuit en série :

\displaystyle Z=\sqrt{R^2+\left(L \,ω-\frac{1}{C \,ω}\right)^2}

où

R

est la résistance totale,

L

est l’inductance,

C

est la capacité et

ω=2π \,f

est la pulsation du courant sinusoïdal (de fréquence

f

).

En outre, le déphasage

ϕ

de la tension aux bornes de l’ensemble, par rapport au courant qui circule, est donné par la relation :

\displaystyle \tan(ϕ)=\frac{L \,ω-\frac{1}{C \,ω}}{R}

.

En mesurant différentes tensions pour différentes fréquences du régime sinusoïdal, on se propose :

◊ de vérifier expérimentalement la validité de ces relations ;
◊ de tester si elles permettent de mesurer les caractéristiques

r

L

C

des bobines et condensateurs.

2. Manipulation

2.1. Réglages préalables

• Effectuer les réglages de base de l'oscilloscope, sans oublier de vérifier que les interrupteurs des voies

A

B

sont en position “entrée directe”, que les calibres sont en position “calibrée” et que la synchronisation automatique n’est pas en mode “alterné”.

2.2. Rappel : mesure des déphasages

• Pour mesurer la phase sur l'écran de l'oscilloscope, on peut repérer le décalage des maxima en proportion d'une période (

2π \:\mathrm{rad}

) :

ou bien repérer le décalage des passage par zéro (seulement si les signaux sont bien centrés) :

• Les mesures sur l’écran sont généralement moins précises que celles effectuées avec un phasemètre. La connaissance de la méthode est toutefois souhaitable pour pouvoir vérifier sur l'écran les mesures qui semblent anormales (en cas de mauvais déclenchement automatique, certains phasemètres peuvent parfois afficher des valeurs fausses).

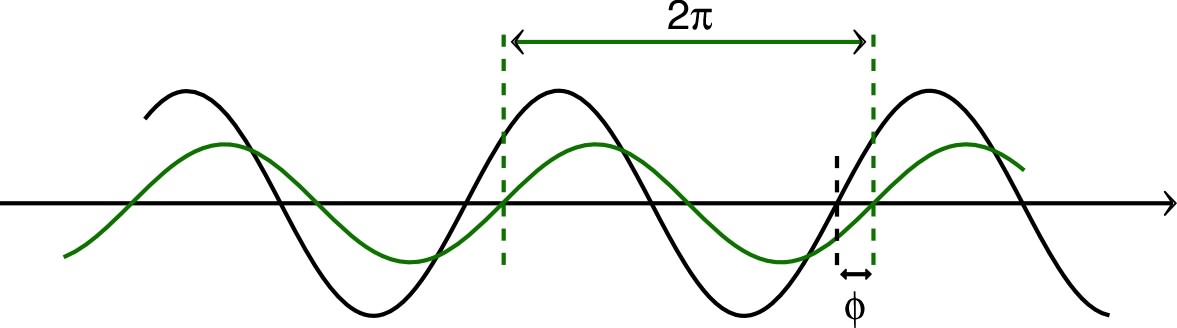
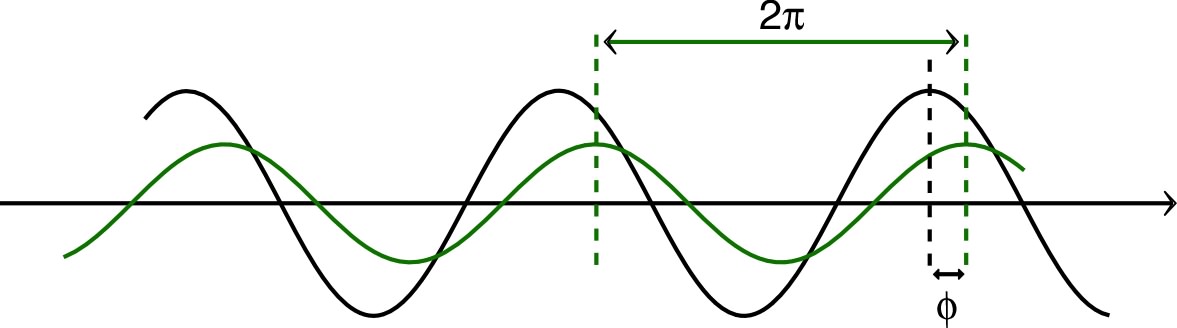
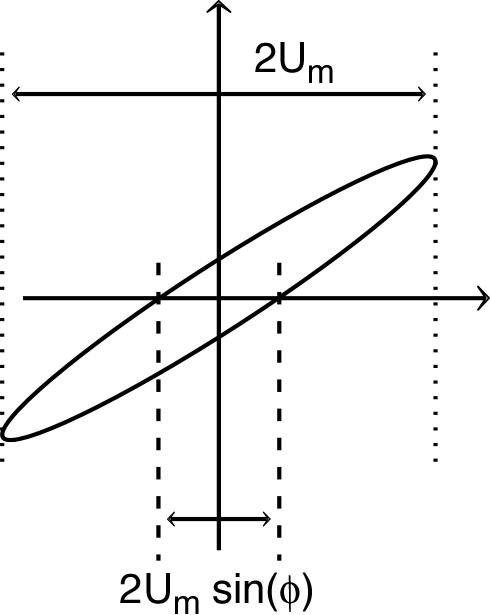
• Au contraire, pour les faibles déphasages, il est souvent plus précis d’utiliser la méthode des “courbes de Lissajous” (mais elle n’indique pas le signe du déphasage).

En mode “XY”, pour deux signaux sinusoïdaux de même fréquence, les courbes de Lissajous sont des ellipses ; la valeur de

\sin(ϕ)

se déduit du rapport entre la largeur de l’intersection avec l’axe et la largeur totale.

◊ remarque : la méthode de Lissajous n'indique pas le signe de

ϕ

car l'ellipse n'en dépend pas ; seul le sens de parcours en dépend mais, sauf à très faible fréquence, l'œil ne distingue pas le mouvement de “rotation” du point lumineux qui trace l'ellipse sur l'écran.

2.3. Circuit RC

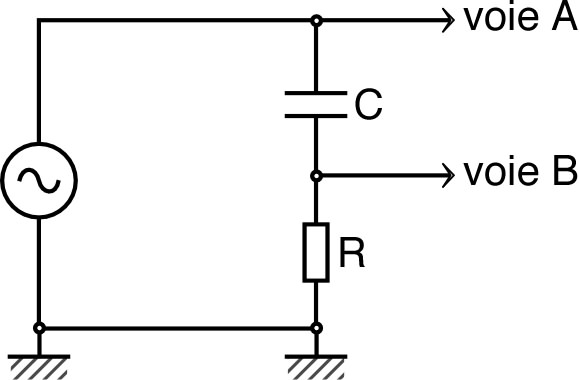
• Réaliser le montage ci-contre avec un résistor de résistance

R≈10 \:\mathrm{kΩ}

et un condensateur de capacité

C≈200 \:\mathrm{nF}

.

◊ remarque : d’une façon générale, il faut ne pas se contenter des indications écrites sur les dipôles (l'incertitude est souvent

≈5 \:%

ou plus) ; mesurer la résistance

R

à l'aide d'un contrôleur électronique et la capacité

C

à l’aide d’un capacimètre.

• Préparer un tableau de mesures de la tension

U_m

fournie par le générateur, de la tension

U_{Rm}

et du déphasage

ϕ

en fonction de la fréquence

f

(mesurée) du signal. Ajouter deux colonnes supplémentaires :

◊ une pour calculer l'impédance en proportion de

R

\displaystyle \frac{Z}{R}=\frac{U_m}{U_{Rm}} =\sqrt{1+\left(\frac{1}{R \,C \,ω}\right)^2}

;
◊ une pour calculer la tangente du déphasage (

ϕ<0

dans ce cas) :

\tan(ϕ)

◊ remarque : pour les tensions, on peut aussi bien mesurer les valeurs efficaces (leur rapport est le même) ; en régime sinusoïdal, elle sont égales aux valeurs maximum divisées par

\sqrt{2}

.

• Effectuer une série de mesures pour des fréquences

f

environ réparties entre

50 \:\mathrm{Hz}

2 \:\mathrm{kHz}

(par exemple :

\mathbf{\underline{50 \:Hz}}

;

75 \:\mathrm{Hz}

;

\underline{100 \:\mathrm{Hz}}

;

150 \:\mathrm{Hz}

;

200 \:\mathrm{Hz}

;

\mathbf{\underline{300 \:Hz}}

;

400 \:\mathrm{Hz}

;

\underline{600 \:\mathrm{Hz}}

;

1000 \:\mathrm{Hz}

;

1500 \:\mathrm{Hz}

;

\mathbf{\underline{2000 \:Hz}}

).

Pour chaque fréquence, mesurer :

◊ la fréquence (précisément, mais sans perdre de temps à essayer d'imposer une valeur précise :

\text{51,32} \:\mathrm{Hz}

est tout aussi acceptable que

\text{50,00} \:\mathrm{Hz}

) ;
◊ les deux tensions

U

U_R

(maximum ou efficace) ;
◊ leur déphasage.

☞ remarque : avant d’effectuer toute série de mesures, il est préférable de commencer par s’assurer que le comportement global du montage est bien celui désiré ; pour cela, le plus simple est de mesurer d’abord les deux extrêmes (ici

50 \:\mathrm{Hz}

2000 \:\mathrm{Hz}

) puis une valeur moyenne (ici

300 \:\mathrm{Hz}

), puis de placer ces points sur un graphique ; c’est seulement ensuite, si l’allure est correcte, qu’on peut améliorer la série en effectuant les autres mesures intermédiaires.

• Représenter

\displaystyle y=\left(\frac{Z}{R}\right)^2

en fonction de

\displaystyle x=\frac{1}{ω^2}

; ajouter éventuellement quelques mesures pour améliorer le graphique ; vérifier la validité de la relation

\displaystyle \left(\frac{Z}{R}\right)^2=1+\frac{1}{R^2 \,C^2 \,ω^2}

et en déduire la valeur de

C

.

• Représenter

y=\tan(ϕ)

en fonction de

\displaystyle x=\frac{1}{ω}

; vérifier la validité de la relation

\displaystyle \tan(ϕ)=-\frac{1}{R \,C \,ω}

et en déduire la valeur de

C

.

• Comparer : la valeur mesurée par un capacimètre, la valeur indiquée sur le condensateur, les valeurs

C

résultant des deux calculs précédents.

◊ remarque : dans cette manipulation, l'étude du déphasage apporte autant d'information que l'étude des amplitudes : elle permet la mesure d'une grandeur caractéristique du condensateur (la capacité

C

2.4. Circuit RL

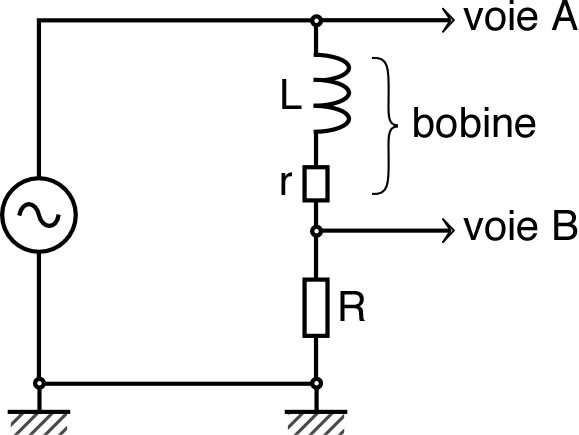
• En modifiant un peu la méthode, comme cela est indiqué dans la suite, reprendre la même manipulation pour le montage suivant, réalisé avec un résistor de résistance

R≈100 \:\mathrm{Ω}

et une bobine d'inductance

L≈50 \:\mathrm{mH}

et de résistance

r

.

◊ remarque : mesurer le valeurs des résistances

R

r

à l'aide d'un contrôleur électronique, celle de

L

à l’aide d’un inductancemètre).

• Représenter

\displaystyle y=\left(\frac{Z}{R}\right)^2

en fonction de

x=ω^2

; ajouter éventuellement quelques mesures pour améliorer le graphique ; vérifier la validité de la relation

\displaystyle \left (\frac{Z}{R}\right)^2=\left(\frac{R+r}{R}\right)^2+\frac{L^2 \,ω^2}{R^2}

et en déduire les valeurs de

L

r

. Comparer avec les valeurs indiquées sur la bobine, etc…

• Représenter

y=\tan(ϕ)

en fonction de

x=ω

; vérifier la validité de la relation

\displaystyle \tan(ϕ)=\frac{L ω}{R+r}

et en déduire la valeur du quotient

\displaystyle \frac{L}{R+r}

. Comparer ces résultats aux précédents, etc…

◊ remarque : dans cette manipulation, l'étude du déphasage apporte moins d'information que l'étude des amplitudes : elle permet la mesure d'une relation entre

L

r

(en fonction de

R

), mais ne permet pas la mesure des deux grandeurs caractéristiques de la bobine (l'inductance

L

et la résistance

r

RÉGIME SINUSOÏDAL ; IMPÉDANCES - TP1

Matériel

Pour chaque groupe (10 groupes)

1 oscilloscope
1 générateur BF
1 fréquencemètre
1 phasemètre
3 adaptateurs BNC/“fiches

4 \:\mathrm{mm}

”
12 fils (des longs et des courts)
2 câbles coaxiaux (BNC d’un seul côté)
2 câbles coaxiaux (BNC des deux côtés)
1 raccord BNC “en T”
1 prolongateur “fiches

4 \:\mathrm{mm}

”
2 contrôleurs électroniques
1 condensateur

≈ 200 \:\mathrm{nF}

1 boite de condensateurs

1

10 \:\mathrm{μF}

1 boite de résistors

×1

×1000 \:\mathrm{Ω}

1 bobine d’inductance

≈ 10

50 \:\mathrm{mH}