◊ remarque : utiliser des résistances différentes, mais du même ordre de grandeur, entre et (par ailleurs pour la sortie du générateur B.F.).
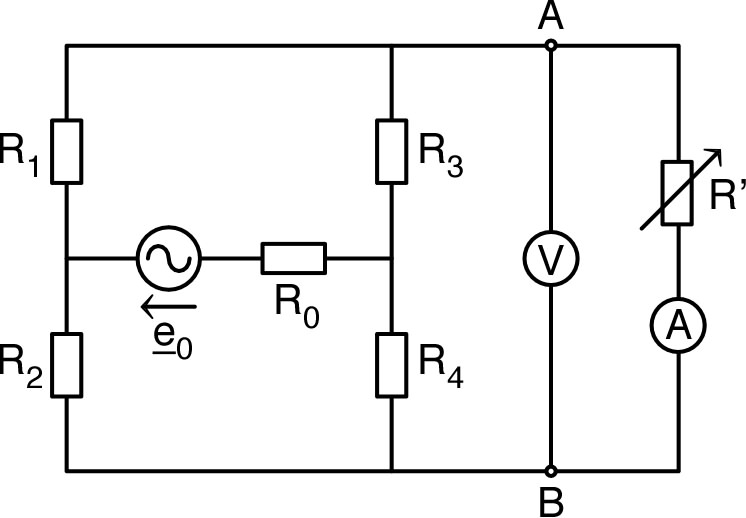
| • Après avoir mesuré, à l'aide d'un
ohm-mètre électronique, la résistance de chacun des
résistors utilisés, réaliser le circuit ci-contre. ◊ remarque : utiliser des résistances différentes, mais du même ordre de grandeur, entre et (par ailleurs pour la sortie du générateur B.F.). |
 |
|
; ; . |
| • Le montage ci-contre (simple pont
diviseur de tension) permet de mesurer précisément la
résistance et l'inductance d'une bobine, à condition
d'utiliser des voltmètres “parfaits” (d'impédance d'entrée
très grande). Il peut être réalisé (selon le groupe de TP) avec une bobine :
◊ remarque : mesurer au préalable (avec un inductance-mètre) et (avec un ohm-mètre) : ceci donne une mesure précise à “basse” fréquence. • En “équilibrant” le pont par la méthode décrite ci-après, on veut ainsi mesurer et en fonction de la fréquence du générateur B.F. (depuis jusqu'à si possible). ◊ remarque : il faut des capacités de à . |
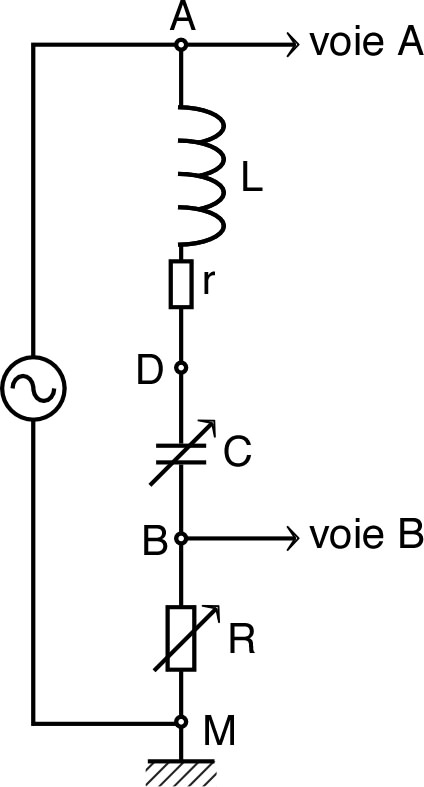 |
| ◊ ajuster pour
obtenir que les deux tensions soient en phase (on observe un
segment de droite en diagonale) ; on en déduit alors
:
; ◊ le circuit étant alors purement résistif (pont diviseur de tension) : donc . |
| ◊ remarque : certains manuels d'électrocinétique proposent le montage ci-contre (pont de Hay-Maxwell), dont l'équilibre correspond à : avec et d'où on déduit : et ; les montages de ce type (où l'équilibre est repéré par un zéro du détecteur) étaient indispensables quand on ne disposait pas de voltmètres “parfaits”, mais ils sont inutilement difficiles à équilibrer (les inévitables parasites compliquent l'observation d'un signal nul). | 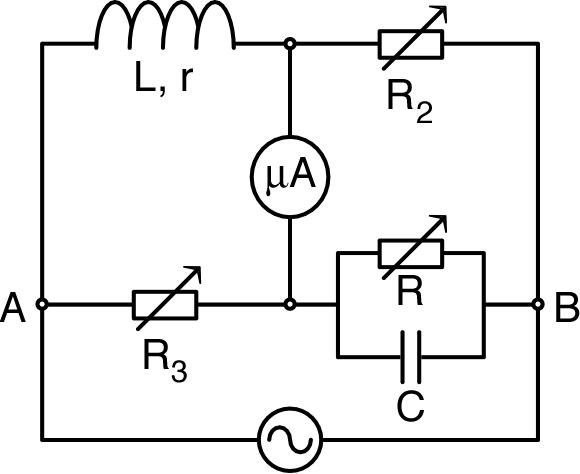 |