RÉGIME SINUSOÏDAL - NOTION D’IMPÉDANCE

RÉGIME SINUSOÏDAL - NOTION D’IMPÉDANCE - corrigé des exercices

A. EXERCICES DE BASE

I. Réalisation d'un champ tournant

• La première bobine crée un champ magnétique :

\overset{⟶}{B_1}=B_m \; \cos(ω_0 \, t) \; \overset{⟶}{u_x}

(par symétrie, le champ créé sur l'axe de la bobine est parallèle à l'axe

Ox

; en outre, il est proportionnel au courant dans la bobine).
• La seconde bobine crée un champ de même norme maximum

B_m

(les bobines, les courants et les distances sont les mêmes), mais perpendiculaire au précédent et en avance de

\frac{π}{2}

\overset{⟶}{B_2}=±B_m \; \cos\left(ω_0 \, t+\frac{π}{2}\right) \;\overset{⟶}{u_y} =±B_m \; \sin(ω_0 \, t) \;\overset{⟶}{u_y}

◊ remarque : au fur et à mesure que le condensateur se charge, la tension disponible pour la bobine diminue plus tôt (et inversement pour la décharge), donc

\overset{⟶}{B_2}

serait a priori en avance sur

\overset{⟶}{B_1}

(pour

ω_0 \, t=0

, sa phase étant déjà à

\frac{π}{2}

) ; mais le schéma simplifié n'indique pas dans quel sens se fait l'enroulement des spires des bobines, donc on ne connait pas vraiment le sens du champ magnétique.
• Le champ total est ainsi :

\overset{→}{B}=B_m \:\left[\cos(ω_0 \, t) \;\overset{⟶}{u_x} ±\sin(ω_0 \, t) \;\overset{⟶}{u_y} \right]=B_m \: \overset{→}{v}

orienté selon le vecteur unitaire

\overset{→}{v}=\cos(ω_0 \, t) \;\overset{⟶}{u_x} ±\sin(ω_0 \, t) \;\overset{⟶}{u_y}

qui tourne à la vitesse angulaire

±ω_0

• Puisque la tension appliquée aux deux branches est la même, les conditions précédentes imposent pour celles-ci des impédances complexes :

◊ de même module :

\displaystyle \left|R+\mathrm{j}Lω_0 \right|=\left|R+R'+\mathrm{j} .\left(Lω_0-\frac{1}{Cω_0}\right)\right|

;
◊ déphasées de

\frac{π}{2}

\displaystyle \tan(ϕ_1)=-\frac{1}{\tan(ϕ_2)}

ce qui peut s'écrire :

\displaystyle \frac{Lω_0}{R}=-\frac{R+R'}{Lω_0-\frac{1}{Cω_0}}

• La résolution du système d'équations donne :

Lω_0=R+R'

\displaystyle R=\frac{1}{Cω_0}-Lω_0

d’où on déduit :

\displaystyle C=\frac{1}{ω_0∙(Lω_0+R)}

R'=Lω_0-R

.
◊ remarque : on constate en particulier que le montage n'est possible que si

R≤Lω_0

II. Pont de Wheatstone en régime alternatif

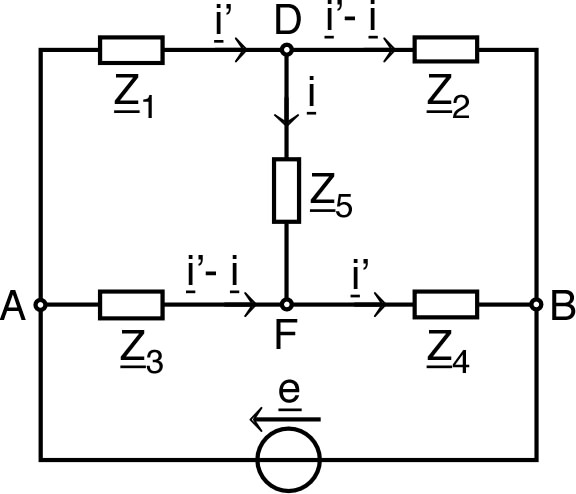
• La condition “usuelle” d'équilibre du pont correspond à :

\underline{Z}_1 \:\underline{Z}_4=\underline{Z}_2 \:\underline{Z}_3

avec les notations suivantes.

• Dans le cas étudié ici, cela correspond à :

\displaystyle (\mathrm{j}Lω)^2=\frac{1}{(\mathrm{j}Cω)^2}

c'est-à-dire à :

(LCω^2)^2=1

, ce qui est vérifié. Par conséquent, il peut sembler logique de considérer que

\underline{i}=0

dans

\underline{Z}_5=R

• Compte tenu de la symétrie centrale (

\underline{Z}_1=\underline{Z}_4=\mathrm{j}Lω

\displaystyle \underline{Z}_2=\underline{Z}_3=\frac{1}{\mathrm{j}Cω}

), le courant est le même respectivement dans les deux bobines et dans les deux condensateurs.
• En appliquant la loi des mailles, avec la condition donnée par l'énoncé (

\displaystyle \mathrm{j}Lω=-\frac{1}{\mathrm{j}Cω}

), on obtient :

-\underline{e}-\mathrm{j}Lω.(\underline{i}'-\underline{i})+\mathrm{j}Lω \: \underline{i}'=0

\mathrm{j}Lω \: \underline{i}'+R \:\underline{i}+\mathrm{j}Lω.(\underline{i}'-\underline{i})=0

; on en déduit :

\displaystyle \underline{i}=\frac{\underline{e}}{\mathrm{j}Cω}=-\mathrm{j}Cω \:\underline{e}

• La contradiction apparente vient du fait qu'on a utilisé sans précaution la condition “usuelle” d'équilibre du pont ; cette condition correspond en fait à annuler le numérateur de l'expression générale de

\underline{i}

, mais cela n'est cohérent que dans les cas où le dénominateur est non nul. Or, le cas présent nécessite de refaire le calcul car la condition d'équilibre correspond à la résonance. C'est donc logiquement la seconde méthode qui aboutit à la bonne réponse dans la mesure où elle reprend un calcul plus complet.
• Pour s'en convaincre, on peut refaire le calcul par une troisième méthode (par exemple à l'aide du théorème de Thévenin), avec des bobines de résistances

r

, puis considérer la limite

r→0

. Pour cela, on remplace la partie du réseau complémentaire de

R

par un générateur de Thévenin de force électromotrice

\underline{e}'

et d'impédance

\underline{Z}'

.
• La f.e.m.

\underline{e}'

est égale à la tension “à vide” (en l'absence de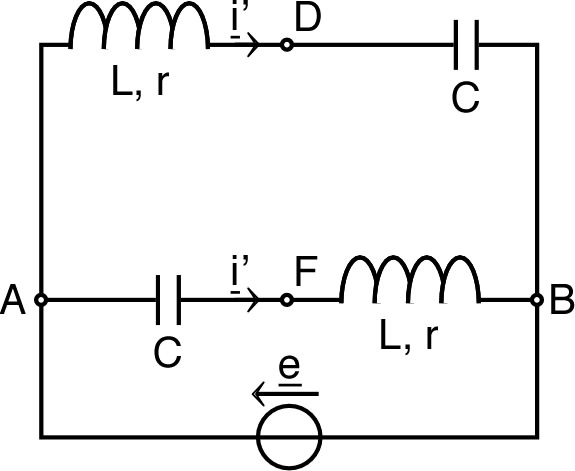

R

Or, la loi des mailles donne :

\displaystyle -\underline{e}+\left(r+\mathrm{j}Lω+\frac{1}{\mathrm{j}Cω}\right) \;\underline{i}'=0

d'où on déduit (en simplifiant) :

\displaystyle \underline{i}'=\frac{\underline{e}}{r}

. On calcule ensuite :

\displaystyle \underline{e}'=\underline{u}_{DF}=\left(-r-\mathrm{j}Lω+\frac{1}{\mathrm{j}Cω}\right) \; \underline{i}'=-\underline{e} \, \frac{r+2\,\mathrm{j}Lω}{r}

.
• L'impédance

\underline{Z}'

est égale à l'impédance du même circuit, avec générateur à l'arrêt (

\underline{e}=0

, ce qui correspond à le court-circuiter).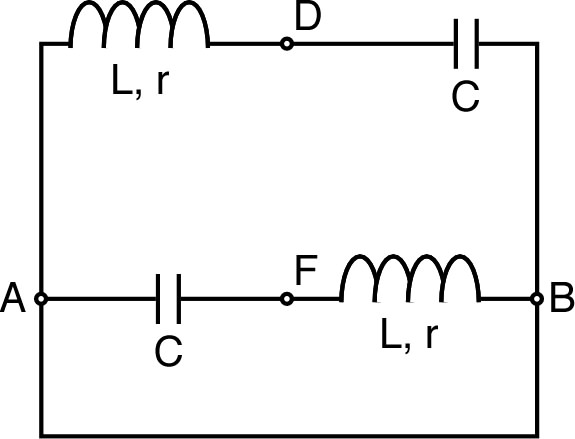

Or, cette résistance correspond à deux assemblages en série avec pour chacun

r+\mathrm{j}Lω

en parallèle avec

\displaystyle \frac{1}{\mathrm{j}Cω}

\displaystyle \underline{Z}'=\frac{2}{\frac{1}{r+\mathrm{j}Lω}+\mathrm{j}Cω}=-2 \,\frac{r+\mathrm{j}Lω}{r} \: \mathrm{j}Lω

.
• On obtient donc finalement :

\displaystyle \underline{i}=\frac{\underline{e}'}{R+\underline{Z}'}=-\underline{e} \; \frac{r+2\,\mathrm{j}Lω}{R \:r-2 \,(r+\mathrm{j}Lω) \: \mathrm{j}Lω}

. Dans la limite où

r→0

, on obtient :

\displaystyle \underline{i}→\frac{\underline{e}}{\mathrm{j}Lω}=-\mathrm{j}Cω \:\underline{e}

; mais il faut noter que dans ces mêmes conditions :

\underline{e}'→∞

\underline{Z}'→∞

(d'où le résultat incohérent si on simplifie n'importe comment).

III. Pont en “P/Q” et pont en “PQ”

• Pour le pont en “P/Q”, la condition d’équilibre s’écrit :

P \:\underline{Z}_0=Q \:\underline{Z}

, c’est-à-dire que :

\displaystyle \underline{Z}=\underline{Z}_0 \, \frac{P}{Q}

a le même argument que

\underline{Z}_0

; il s’agit donc d’impédances de même nature.
• Pour le pont en “PQ”, la condition d’équilibre s’écrit :

P \:Q=\underline{Z} \: \underline{Z}_0

, c’est-à-dire que :

\displaystyle \underline{Z}=\frac{P \:Q}{\underline{Z}_0}

a un argument de signe contraire à celui de

\underline{Z}_0

; il s’agit donc d’impédances de nature différente (capacités et inductances).

IV. Équation différentielle

1.a.	• Les relations sont : $i_c=i+i_1+i_2$ ; $\displaystyle R \:i=\frac{q_1}{C}=R \:i_2+\frac{q_2}{C}$ ; $i_1=\dot{q_1}$ ; $i_2=\dot{q_2}$ .

1.b.	• En éliminant les charges (et en posant $τ=R\,C$ ) : $τ \:\dot{[i]}=i_1=τ \:\dot{[i_2 ]}+i_2$ . • On en déduit l'équation différentielle : $τ \:\dot{[i_c ]}=(τ \:\dot{[i_2 ]}+i_2 )+τ .\left[\dot{\overbrace{τ \:\dot{[i_2 ]}+i_2}} \right] ̇+τ \:\dot{[i_2 ]}$ qui peut s'écrire en simplifiant : $τ^2 \:\ddot{[i_2 ]}+3 \,τ \:\dot{[i_2 ]}+i_2=τ \:\dot{[i_c ]}$ .

2.a.	• En considérant un pont diviseur de courant : $\displaystyle \underline{i}_2=\underline{i}_c \: \frac{\underline{Y}_2}{\underline{Y}+\underline{Y}_1+\underline{Y}_2}$ avec $\displaystyle \underline{Y}=\frac{1}{R}$ ; $\underline{Y}_1=\mathrm{j}Cω$ ; $\displaystyle \underline{Y}_2=\frac{1}{R+\frac{1}{\mathrm{j}Cω}}$ ; c'est-à-dire : $\displaystyle \underline{i}_2=\underline{i}_c \:\frac{\mathrm{j} ωτ}{(\mathrm{j} ωτ)^2+3\,\mathrm{j} ωτ+1}$ .

2.b.	• La relation précédente peut s'écrire : $((\mathrm{j} ωτ)^2+3\,\mathrm{j} ωτ+1) \: \underline{i}_2=\mathrm{j} ωτ \:\underline{i}_c$ ; mais en régime sinusoïdal la multiplication par $\mathrm{j}ω$ correspond à une dérivation, donc on retrouve : $τ^2 \:\ddot{[i_2 ]}+3 \,τ \:\dot{[i_2 ]}+i_2=τ \:\dot{[i_c ]}$ . ◊ remarque : on peut vérifier que le régime continu correspond à $i_2=0$ pour le circuit considéré. ◊ remarque : cette équation étant valable pour tout régime sinusoïdal, elle est en fait aussi valable pour tout régime variable car la “transformation de Fourier” permet de décomposer tout signal en une somme (intégrale) de signaux sinusoïdaux ; ainsi le raisonnement précédent n'est pas seulement une astuce pour trouver plus simplement l'équation, c'est en outre une démonstration.

B. EXERCICE D'APPROFONDISSEMENT

V. Transformée de Fourier

1.a.

• On obtient par linéarité de l'intégrale :

\displaystyle ∫_{-∞}^∞ [λ \:f(t)+μ \:g(t)] \; \mathrm{e}^{-\mathrm{j}ω t} \; dt=λ \;∫_{-∞}^∞ f(t) \;\mathrm{e}^{-\mathrm{j}ω t} \; dt+μ \;∫_{-∞}^∞ g(t) \;\mathrm{e}^{-\mathrm{j}ω t} \; dt

1.b.

• Avec

u=α \:t

on obtient (en rectifiant au besoin les bornes selon

\mathrm{sgn}(α)

) :

\displaystyle ∫_{-∞}^∞ f(α \:t) \;\mathrm{e}^{-\mathrm{j}ω t} \; dt=∫_{-∞}^∞ f(u) \;\mathrm{e}^{-\mathrm{j}ω \,u/α} \; \frac{du}{|α|}=\frac{1}{|α|}\, ∫_{-∞}^∞ f(u) \;\mathrm{e}^{-\mathrm{j}\,(ω/α)\, u} \; du=\frac{1}{|α|} \, φ\left(\frac{ω}{α}\right)

1.c.

• Avec

u=t+t_0

on obtient :

\displaystyle ∫_{-∞}^∞ f(t+t_0) \;\mathrm{e}^{-\mathrm{j}ω t} \; dt=∫_{-∞}^∞ f(u) \;\mathrm{e}^{-\mathrm{j}ω \,(u-t_0 )} \; du=∫_{-∞}^∞ f(u) \;\mathrm{e}^{-\mathrm{j}ω u} \; \mathrm{e}^{\mathrm{j}ω t_0} \; du=\mathrm{e}^{\mathrm{j}ω t_0} \; φ(ω)

1.d.

• On obtient :

\displaystyle ∫_{-∞}^∞ [f(t) \;\mathrm{e}^{\mathrm{j}ω_0 t}\, ] \; \mathrm{e}^{-\mathrm{j}ω t} \; dt=∫_{-∞}^∞ f(t) \;\mathrm{e}^{-\mathrm{j}\,(ω-ω_0 ) t} \; dt=φ(ω-ω_0)

1.e.

• On obtient :

\displaystyle ℱ\left\{\frac{df(t)}{dt}\right\}=∫_{-∞}^∞ \left[\frac{df(t)}{dt}\right] \; \mathrm{e}^{-\mathrm{j}ω t} \; dt=\left[f(t) \;\mathrm{e}^{-\mathrm{j}ω t} \right]_{-∞}^∞-∫_{-∞}^∞ f(t) \;\frac{d(\mathrm{e}^{-\mathrm{j}ω t}\,)}{dt} \; dt

;

\displaystyle ℱ\left\{\frac{df(t)}{dt}\right\}=-∫_{-∞}^∞ f(t) \;\frac{d(\mathrm{e}^{-\mathrm{j}ω t}\,)}{dt} \; dt=-∫_{-∞}^∞ f(t)\;[-\mathrm{j}ω \;\mathrm{e}^{-\mathrm{j}ω t} \,] \; dt=\mathrm{j}ω \;φ(ω)

◊ remarque :

\left[f(t) \;\mathrm{e}^{-\mathrm{j}ω t} \right]_{-∞}^∞=0

car la fonction est intégrable (

f(±∞)=0

1.f.

• On obtient :

\displaystyle ℱ\left\{\mathrm{j}t \;f(t)\right\}=∫_{-∞}^∞ f(t) \;\mathrm{j}t \;\mathrm{e}^{-\mathrm{j}ω t} \; dt=-∫_{-∞}^∞ f(t) \;\left[\frac{d(\mathrm{e}^{-\mathrm{j}ω t}\,) }{dω}\right] \; dt

;

\displaystyle ℱ\left\{\mathrm{j}t \;f(t)\right\}=-\frac{d}{dω} \left[∫_{-∞}^∞ f(t) \;\mathrm{e}^{-\mathrm{j}ω t} \; dt\right]=-\frac{dφ(ω)}{dω}

1.g.

• Avec

\displaystyle F(t)=∫_{-∞}^t f(u) \:du

Φ(ω)=ℱ\{F(t)\}

on obtient :

\displaystyle \mathrm{j}ω \;ℱ\left\{∫_{-∞}^t f(u) \:du\right\}=\mathrm{j}ω\;∫_{-∞}^∞ F(t) \:\mathrm{e}^{-\mathrm{j}ω t} \; dt=\mathrm{j}ω \;Φ(ω)=ℱ\left\{\frac{dF(t)}{dt}\right\}=ℱ\{f(t)\}=φ(ω)

• En utilisant (1.c.) on obtient :

\displaystyle ℱ\{h(t)\}=∫_{-∞}^∞ h(t) \;\mathrm{e}^{-\mathrm{j}ω t} \; dt=∫_{-∞}^∞ \left[∫_{-∞}^∞ f(t-τ) \:g(τ) \:dτ\right] \; \mathrm{e}^{-\mathrm{j}ω t} \; dt

;

\displaystyle ℱ\{h(t)\}=∫_{-∞}^∞ \left[∫_{-∞}^∞ f(t-τ) \;\mathrm{e}^{-\mathrm{j}ω t} \; dt\right] \; g(τ) \:dτ=∫_{-∞}^∞ \left[\mathrm{e}^{-\mathrm{j}ω τ} \; ℱ\{f(t)\}\right] \; g(τ) \:dτ

;

\displaystyle ℱ\{h(t)\}=ℱ\{f(t)\} \; ∫_{-∞}^∞ \mathrm{e}^{-\mathrm{j}ω τ} \; g(τ) \:dτ=ℱ\{f(t)\} \; ℱ\{g(t)\}

◊ remarque : inversement

ℱ\{f.\,g\}

s'exprime en fonction de

ℱ\{f\}*ℱ\{g\}

• La transformation inverse montre que

f(t)

peut s'exprimer comme une somme (intégrale) de fonctions de la forme

\mathrm{e}^{\mathrm{j}ωt}

avec des coefficients respectifs

\displaystyle \frac{φ(ω)}{2π}

.
• Dans la mesure où les problèmes étudiés sont linéaires, si on connait une solution pour chacun de ces termes exponentiels, alors la solution globale s'obtient par une somme (intégrale) des solutions partielles pondérées par les coefficients respectifs.
• Les formes sinusoïdales pouvant se ramener à des exponentielles du type considéré, l'étude du fonctionnement d'un réseau en régime sinusoïdal permanent permet en principe d'en déduire son comportement en régime quelconque.

4.a.	• L'équation peut s'écrire : $\displaystyle e=L \,\frac{di}{dt}+R \:i+ \frac{1}{C} \, ∫ i \:dt$ .

4.b.	• On obtient : $\displaystyle ℰ=(\mathrm{j}ωL+R+\frac{1}{\mathrm{j}ωC}) \; ℐ$ ; même relation que celle entre représentants complexes. • Pour résoudre le problème par l'intermédiaire de la transformation de Fourier, on est toutefois ramené à étudier le cas où $ℰ$ est la transformée d'une exponentielle $\mathrm{e}^{±\mathrm{j}ωt}$ ) ; or on ne peut pas simplement considérer qu'il s'agit d'une fonction intégrable : cela nécessite une généralisation non évidente (c'est intégrable au sens des “distributions”). C'est pourquoi il est ici plus simple d'utiliser une transformation analogue : celle de Laplace. ◊ remarque : la “distribution” delta est une généralisation de la notion de fonction, définie par son comportement dans les intégrales : $\displaystyle ∫_{-∞}^∞ δ(x) \:f(x) \:dx=f(0)$ ; le régime sinusoïdal amène à considérer : $ℰ=ℱ\{E_m \; \mathrm{e}^{\mathrm{j}ω_0 t}\, \}=2π \:E_m \; δ(ω-ω_0 )$ ; avec la transformée inverse : $\displaystyle \underline{i}=\tilde{ℱ}\left\{\frac{ℰ}{\mathrm{j}ωL+R+\frac{1}{\mathrm{j}ωC}}\right\}=\frac{E_m \; \mathrm{e}^{\mathrm{j}ω_0 t}}{\mathrm{j}ω_0 L+R+\frac{1}{\mathrm{j}ω_0 C}}$ ; dans ce cas, il y a plus simple... mais la méthode de Fourier s'applique à toute forme de signal.