RÉGIME SINUSOÏDAL ; IMPÉDANCES - mesures et commentaires du TP1


1. Principe

• Les dipôles électrocinétiques étudiés ne sont décrits qu'en première approximation par les modèles proposés. La modélisation a généralement des limites de validité ; une étude expérimentale permet souvent d'en prendre conscience.


2. Manipulation

2.1. Réglages préalables

• Les appareils électroniques modernes ont l'avantage d'être automatisés, mais quel que soit le niveau de progrès technique, il est indispensable de bien en comprendre le fonctionnement, quitte même à débrayer certains automatismes pour mieux contrôler manuellement.

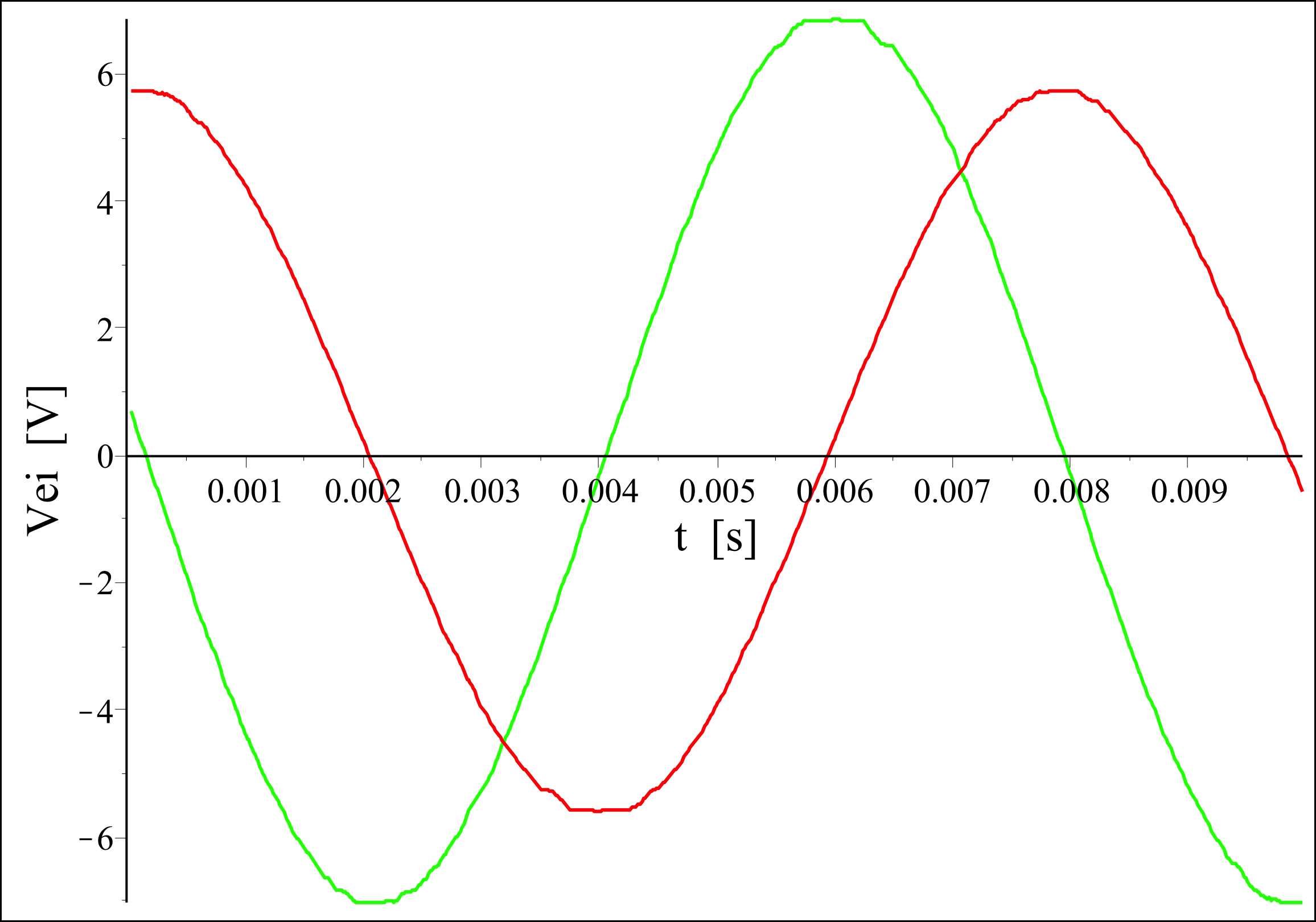
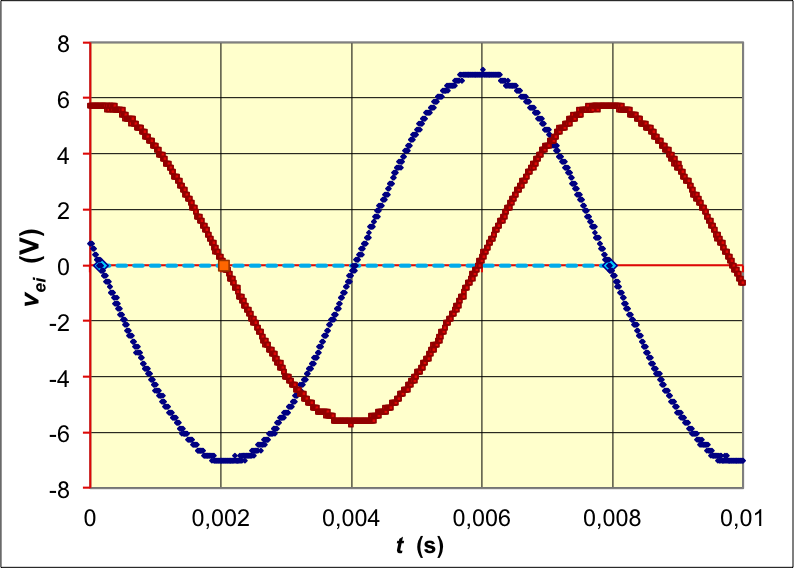
2.2. Mesure des déphasages

• Outre l'utilisation des écrans d'oscilloscopes pour contrôler l'allure correcte ou non des mesures, on peut transférer les mesures aux ordinateurs pour une analyse informatique. De nombreux logiciels permettent ce genre d'étude.

• Ce qui est intéressant ici, c'est la programmation (TP d'informatique) tentant de simuler la détection et la mesure automatique d'un déphasage par le logiciel interne d'un phasemètre numérique (une avec Maple et une autre avec Excel ; cela aurait pu être Python). Pour les mesures du TP, on se limite évidemment à utiliser un phasemètre.

Le logiciel peut être amené à effectuer un lissage modéré avant d'analyser les signaux, par exemple par moyenne “locale” (remplacement de chaque mesure par une moyenne pondérée avec les mesures voisines).

impedance_corTP1_Im/phasemetre_M.png

Le logiciel peut ensuite détecter le minimum et le maximum, puis chercher les passages par la moyenne. Détectant le sens de variation lors des passages, il peut repérer la périodicité sur chacun des deux signaux, en vérifier la compatibilité, puis calculer le décalage en proportion d'une période ; de nombreuses méthodes peuvent être utilisées pour programmer cela.

L'exemple Maple calcule  T=7,89±0,09msT=\text{7,89}±\text{0,09} \:\mathrm{ms}  puis  ϕ=−86,2±1,0°ϕ=-\text{86,2}±\text{1,0} \:°  (−1,51±0,02rad-\text{1,51}±\text{0,02} \:\mathrm{rad} ).

L'exemple Excel calcule  T=7,80±0,09msT=\text{7,80}±\text{0,09} \:\mathrm{ms}  puis  ϕ=−87,5±1,0°ϕ=-\text{87,5} ± \text{1,0} \:°  (−1,53±0,02rad-\text{1,53} ± \text{0,02} \:\mathrm{rad} ).

◊ remarque : on pourrait aussi programmer pour vérifier que la période détectée se reproduit effectivement.

impedance_corTP1_Im/phasemetre_E.png

• Une autre démarche consiste à effectuer un ajustement (séparé ou global) de deux sinusoïdes (ce qui privilégie cette forme de signaux) et de leur déphasage.

L'exemple Maple calcule une période  T=7,800±0,003msT=\text{7,800}±\text{0,003} \:\mathrm{ms}  (mais en supposant que la forme est effectivement sinusoïdale) puis un déphasage  ϕ=−86,15±0,11°ϕ=-\text{86,15}±\text{0,11} \:°  (−1,521±0,002rad-\text{1,521}±\text{0,002} \:\mathrm{rad} ).

L'exemple Excel calcule une période  T=7,80±0,01msT=\text{7,80}±\text{0,01} \:\mathrm{ms}  (mais en supposant que la forme est effectivement sinusoïdale) puis un déphasage  ϕ=−87,3±1,1°ϕ=-\text{87,3}±\text{1,1} \:°  (−1,52±0,02rad-\text{1,52}±\text{0,02} \:\mathrm{rad} ).

La précision apparente apportée par la contrainte sinusoïdale doit ici être surveillée, car il est peu probable que les signaux soient totalement exempts de parasites : le supposer peut introduire de fait une cause d'incertitudes systématiques.

◊ remarque : à part pour les déphasages faibles, pour lesquels les phasemètres ont souvent une précision relative modeste, la lecture sur l'écran de l'oscilloscope est généralement moins précise et ne sert que pour contrôler si les mesures affichées par le phasemètre sont plausibles.

2.3. Circuit RC

• Le montage est réalisé avec un résistor de résistance  R=9960±52ΩR=9960±52 \:\mathrm{Ω}  et un condensateur de capacité  C≈205,0±2,3nFC≈\text{205,0}±\text{2,3} \:\mathrm{nF} .

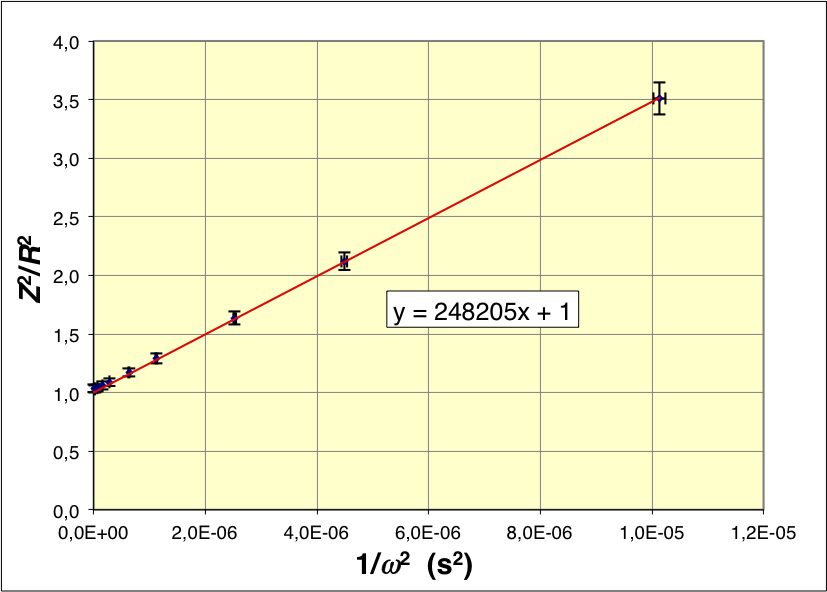
impedance_corTP1_Im/RC1.png

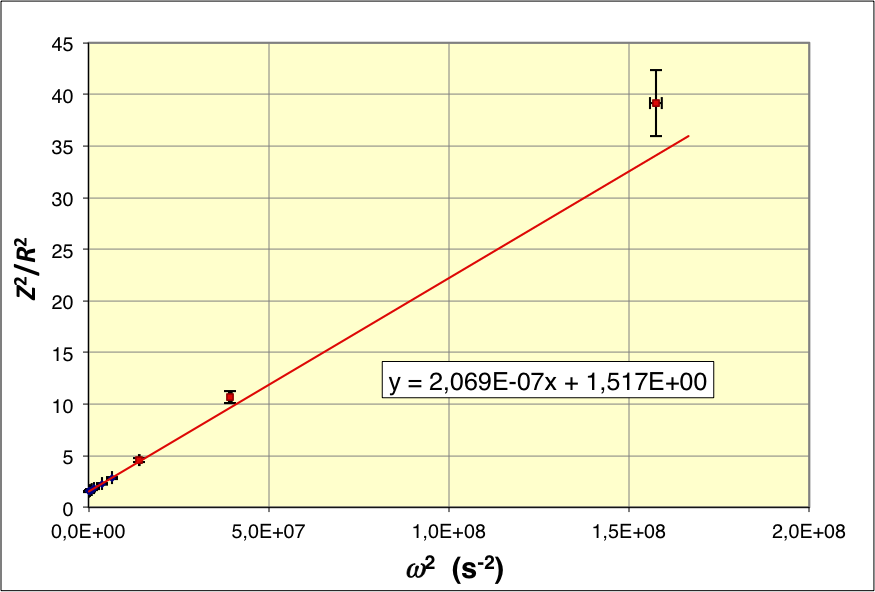
• Les mesures obtenues donnent une représentation affine conforme à la relation  (ZR)2=1+1R2C2ω2\displaystyle \left(\frac{Z}{R}\right)^2=1+\frac{1}{R^2 \,C^2 \,ω^2} .

La pente correspond à  1R2C2=(248±5).103s−2\displaystyle \frac{1}{R^2 \,C^2}=(248±5).{10}^3 \: \mathrm{s^{-2}}  tout à fait compatible avec les valeurs préalablement mesurées :  1R2C2=(240±8).103s−2\displaystyle \frac{1}{R^2 \:C^2}=(240±8).{10}^3 \: \mathrm{s^{-2}} .

Inversement, si on suppose connue la résistance (c'est le cas pour celle contenue dans le circuit de mesure d'un capacimètre), on peut en déduire la valeur de la capacité :  C=202±3nFC=202±3 \:\mathrm{nF} .

◊ remarque : pour estimer rapidement les incertitudes de mesure, voir le chapitre annexe décrivant les méthodes correspondantes (mais on peut aussi utiliser un logiciel spécialisé).

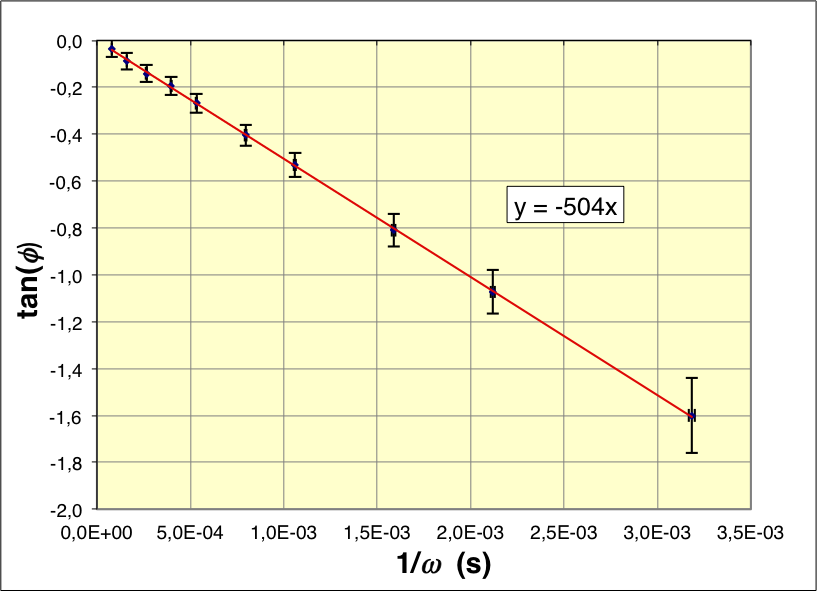
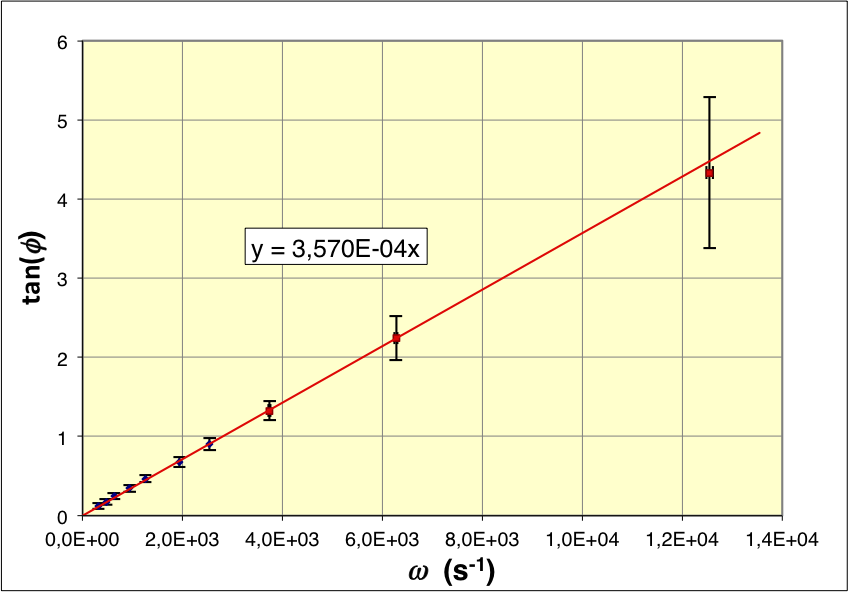
• On obtient également une représentation linéaire conforme à la relation  tan(ϕ)=−1RCω\displaystyle \tan(ϕ)=-\frac{1}{R \,C \,ω} .

impedance_corTP1_Im/RC2.png

La pente correspond à  1RC=504±15s−1\displaystyle \frac{1}{R \,C}=504±15 \:\mathrm{s^{-1}}  tout à fait compatible avec les valeurs préalablement mesurées :  1RC=490±8s−1\displaystyle \frac{1}{R \,C}=490±8 \:\mathrm{s^{-1}} .

Inversement, si on suppose connue la résistance, on en déduit la valeur de la capacité :  C=199±6nFC=199±6 \:\mathrm{nF} .  Ce résultat est toutefois moins précis que celui obtenu par la première méthode.

• La valeur indiquée sur le condensateur (200nF200 \:\mathrm{nF}) n'est qu'approximative (±10%± 10 \:%) ; il faut généralement effectuer une mesure précise. Le circuit étudié ici donne des mesures de précision comparable à celle obtenue avec les circuits intégrés au capacimètre.

2.4. Circuit RL

• Le montage est réalisé avec un résistor de résistance  R=100,0±0,7ΩR=\text{100,0}±\text{0,7} \:\mathrm{Ω}  et une bobine d'inductance  L≈44,4±0,6mHL≈\text{44,4}±\text{0,6} \:\mathrm{mH}  et de résistance  r=22,5±0,3Ωr=\text{22,5}±\text{0,3} \:\mathrm{Ω} .

◊ remarque : il faut éviter les mesures à trop grande fréquence car L L et rr dépendent alors de ωω .

• Les mesures obtenues donnent une représentation affine conforme à la relation  (ZR)2=(R+rR)2+L2ω2R2\displaystyle \left(\frac{Z}{R}\right)^2=\left(\frac{R+r}{R}\right)^2+\frac{L^2 \,ω^2}{R^2}  .

L'ordonnée à l'origine correspond à  (R+rR)2=1,52±0,13\displaystyle \left(\frac{R+r}{R}\right)^2=\text{1,52}±\text{0,13}  tout à fait compatible avec les valeurs préalablement mesurées :  (R+rR)2=1,50±0,02\displaystyle \left(\frac{R+r}{R}\right)^2=\text{1,50}±\text{0,02} .
Inversement, si on suppose connue la résistance RR (c'est le cas pour celle contenue dans le circuit de mesure d'un inductancemètre), on peut en déduire la valeur de la résistance pour la bobine :  r=23±5Ωr=23±5 \:\mathrm{Ω} .  Ce résultat peu précis n'est souvent pas utilisé par l'inductancemètre.

impedance_corTP1_Im/RL1.png

La pente correspond à  L2R2=(2,07±0,03).10−7s2\displaystyle \frac{L^2}{R^2} =(\text{2,07}±\text{0,03}).{10}^{-7} \: \mathrm{s^2}  tout à fait compatible avec les valeurs préalablement mesurées :  L2R2=(1,97±0,08).10−7s2\displaystyle \frac{L^2}{R^2} =(\text{1,97}±\text{0,08}).{10}^{-7} \: \mathrm{s^2} .

Inversement, supposant connue la résistance, on en déduit la valeur de l'inductance :  L=45,5±1,0mHL=\text{45,5}±\text{1,0} \:\mathrm{mH} .

• On obtient également une représentation linéaire conforme à la relation  tan(ϕ)=LωR+r\displaystyle \tan(ϕ)=\frac{L \,ω}{R+r} .

impedance_corTP1_Im/RL2.png

La pente correspond à  LR+r=(3,57±0,08).10−4s\displaystyle \frac{L}{R+r}=(\text{3,57}±\text{0,08}).{10}^{-4} \: \mathrm{s}  tout à fait compatible avec les valeurs préalablement mesurées :  LR+r=(3,62±0,08).10−4s\displaystyle \frac{L}{R+r}=(\text{3,62}±\text{0,08}).{10}^{-4} \: \mathrm{s} .

Par contre, cette relation dépend à la fois de LL et rr, donc elle ne peut pas servir à elle seule pour déterminer ces deux quantités.

• Les valeurs indiquées sur la bobine (45mH45 \:\mathrm{mH} ; 20Ω20 \:\mathrm{Ω}) ne sont qu'approximatives (±10%± 10 \:%) ; il faut généralement effectuer des mesures précises. Le circuit étudié ici donne pour LL des mesures de précision comparable à celle obtenue avec les circuits intégrés à l'inductancemètre ; par contre pour rr les mesures sont généralement plus précises avec un ohm-mètre.