RÉGIME SINUSOÏDAL ; PONTS D’IMPÉDANCES

RÉGIME SINUSOÏDAL ; PONTS D’IMPÉDANCES - corrigé du TP2

1. Représentations de Thévenin et de Norton

• En attende de données fournies par les étudiants...

2. Inductance et résistance d'une bobine

2.1. Capacité parasite entre les spires de la bobine

◊ remarque : cette partie ne décrit pas ce qui est attendu des étudiants, mais décrit au contraire les difficultés d'interprétation qu'il est peu probable qu'ils trouvent sans aide.

• Lorsque la fréquence est assez grande, l'inductance de la bobine tend à empêcher de plus en plus le passage du courant dans les spires (d'autant plus qu'en fait, la résistance augmente aussi à cause de “l'effet de peau” : le courant ne circule qu'au voisinage de la surface des fils).

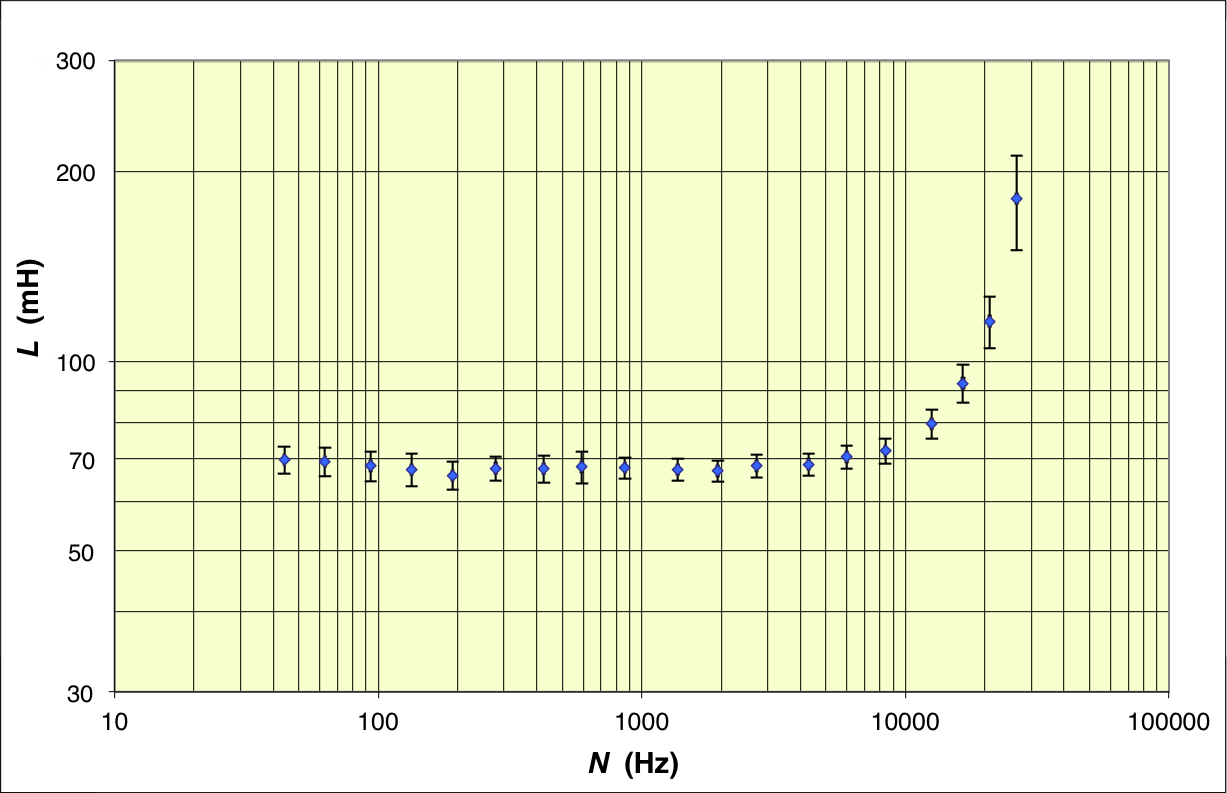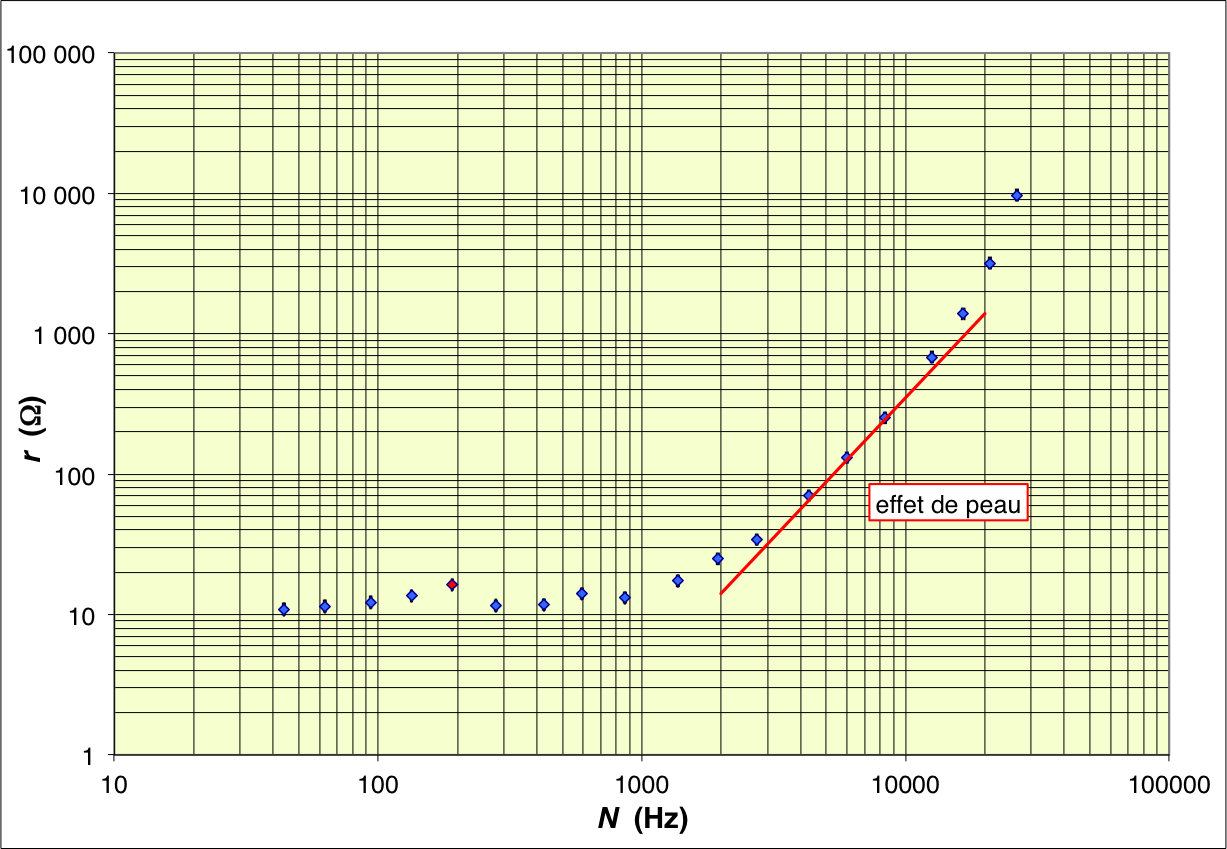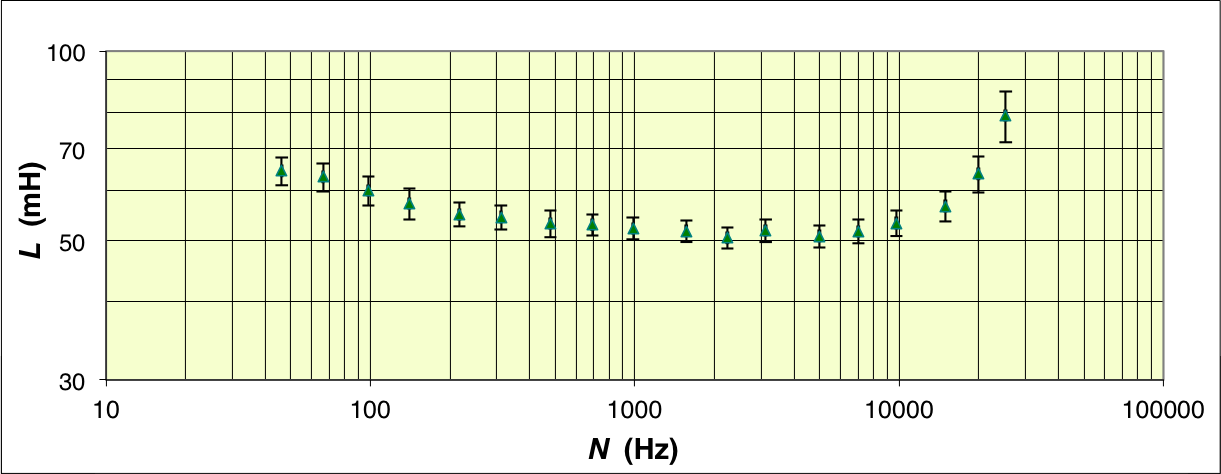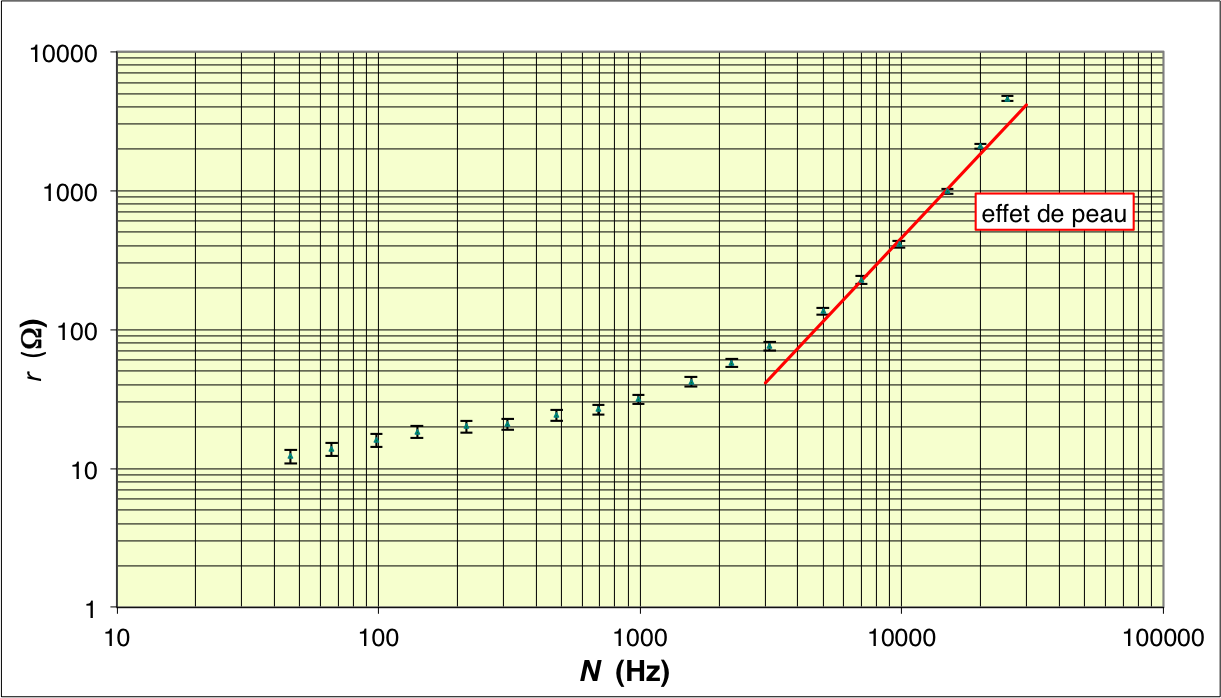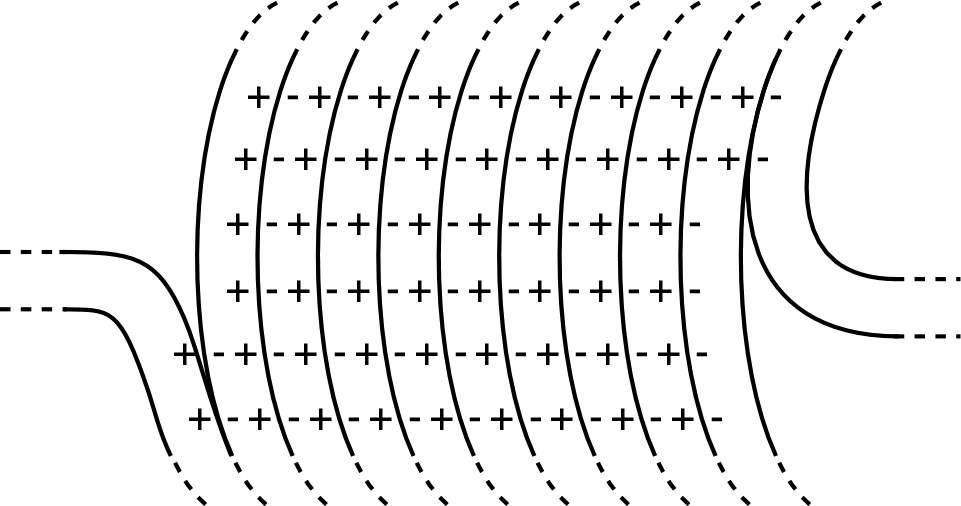
impedance_corTP2_Im/impedance_corTP2_Im1.jpg

• Au contraire, les faces en contact des spires successives (séparées par une couche de vernis) peuvent se polariser comme des condensateurs ; bien que la capacité correspondante soit faible (d'autant plus qu'en série entre elles, ce sont les inverses des capacités qui s'ajoutent), le courant peut alors passer plus facilement par ces condensateurs plutôt qu'en faisant le tour des spires.

Ceci équivaut à un courant qui passe d'une borne à l'autre de la bobine sans passer par les spires, donc à une capacité en parallèle avec le schéma “usuel” de la bobine.

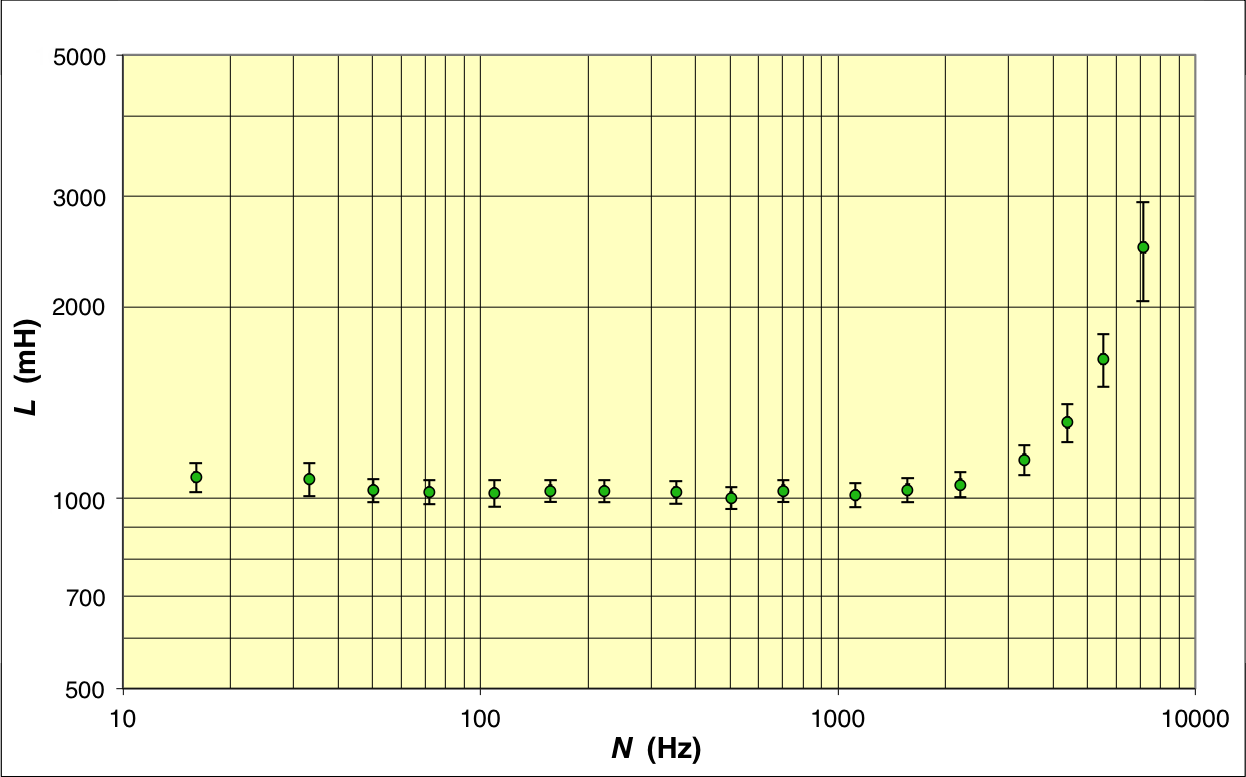
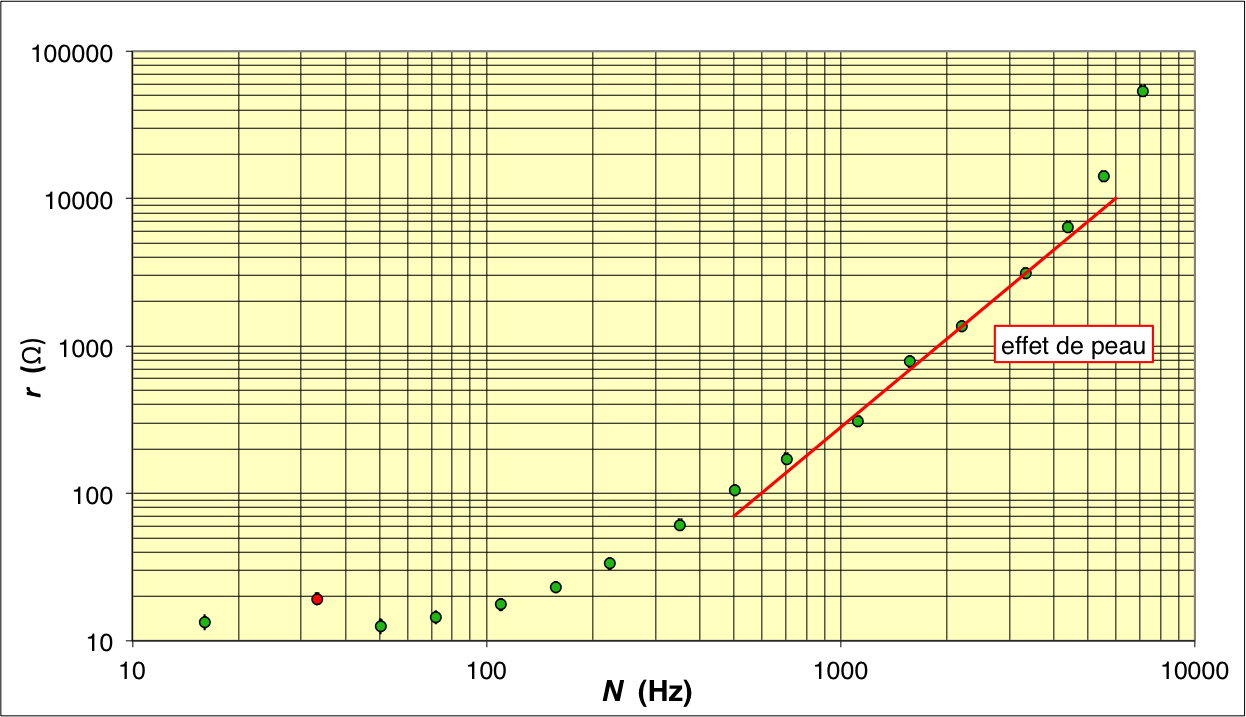
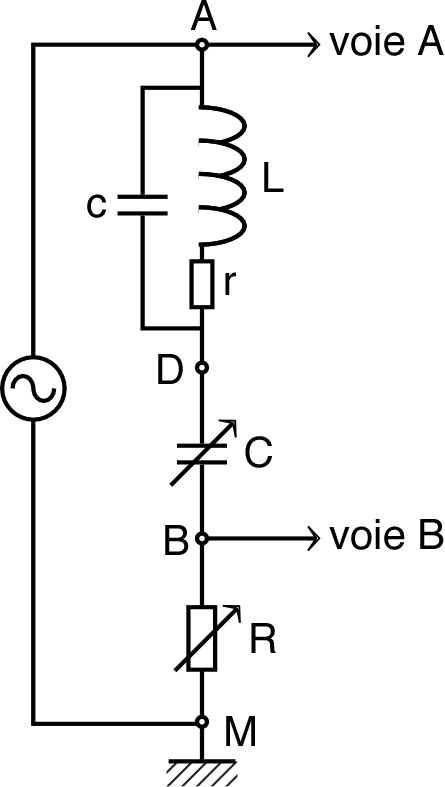
◊ remarque : les charges ne traversent pas l'isolant (un courant continu ne peut pas passer ainsi !), mais la polarisation de chaque spire influence à distance les voisines et cela peut faire passer le courant alternatif à haute fréquence.

• Le montage réel peut donc être décrit de façon plus réaliste par le schéma ci-contre, où on suppose que

L

r

sont des constantes.

L'impédance de la bobine est dans ce cas :

\displaystyle \underline{Z}=\frac{1}{\frac{1}{r+\mathrm{j}Lω}+\mathrm{j}cω}

et l'impédance du pont est :

\displaystyle \underline{Z}_e=\underline{Z}+\frac{1}{\mathrm{j}Cω}+R=\frac{r.(C+c) \:ω+\mathrm{j}\,\left(L.(C+c) \:ω^2-1\right)}{Cω.(1-Lcω^2+\mathrm{j}rcω)}+R

.

• L'équilibre du pont en mode “XY” (impédance réelle) ne correspond plus alors à

\displaystyle L=\frac{1}{C \,ω^2}

mais à :

\displaystyle \frac{L.(C+c) \,ω^2-1}{r.(C+c) \,ω}=\frac{rcω}{1-Lcω^2}

impedance_corTP2_Im/impedance_corTP2_Im3.jpg

• En posant :

α=c.(C+c) \:ω^4

;

β=-(C+2 \,c) \:ω^2

;

γ=1+r^2 \,c.(C+c) \:ω^2

, la relation peut s'écrire :

α \:L^2+β \:L+γ=0

et les solutions (positives) :

\displaystyle L=\frac{-β±\sqrt{β^2-4αγ}}{2\,α}

.

On constate alors que dans la limite des basses fréquences

γ≈1

(à l'ordre le plus bas), ce qui donne après simplification :

\displaystyle L≈\frac{1}{C \,ω^2}

\displaystyle L≈\frac{1}{(C+c) \,ω^2}

.

La première solution (signe +) est sans intérêt car

c

est très petit et ne peut correspondre à un accord avec

ω

petit que si l'inductance est très grande. De plus, même dans ce cas, l'accord ne dépend pas de

C

et ne pourrait donc servir qu'à mesurer

c

quand on connaît déjà

L

.

La solution correspondant à l'accord cherché est donc la seconde :

\displaystyle L=\frac{-β-\sqrt{β^2-4αγ}}{2\,α}

, qui redonne effectivement

\displaystyle L≈\frac{1}{C \,ω^2}

quand

c

est négligeable.

• L'inductance “apparente” calculée par la formule non corrigée est alors fausse. On peut calculer

L_{app}

en fonction de

ω

en supposant

L

r

constantes, puisque l'accord du pont est alors obtenu pour une capacité :

\displaystyle C=\frac{1}{L \,ω^2} \: \frac{(1-Lcω^2 )^2+(rcω)^2}{1-Lcω^2-\frac{r^2 \,c}{L}}

correspondant à :

\displaystyle L_{app}=L \:\frac{1-Lcω^2-\frac{r^2 \,c}{L}}{(1-Lcω^2 )^2+(rcω)^2}

.

On obtient ainsi les variations suivantes (la courbe réelle est en fait légèrement différente, car la résistance n'est pas constante, mais le comportement est globalement le même).

On constate (ce qui est logique) qu'à cause de la capacité parasite la bobine ne se comporte plus comme une bobine au delà de

\displaystyle ω≈\frac{1}{\sqrt{L\,c}}

. Il faut donc ignorer les valeurs de

L

déduites des mesures à trop haute fréquence (plus même : ne pas chercher à utiliser la bobine dans ces conditions) et tenir compte de la capacité parasite pour celles des mesures qui (sans l'atteindre) s'approchent de la fréquence limite.

D'après la forme du numérateur de

L_{app}

, on comprend en outre que cet effet intervient à plus basse fréquence si

r(ω)

augmente à cause de l'effet de peau. Enfin on comprend que l'effet intervient aussi à plus basse fréquence pour les bobines avec noyau (ce dernier augmente la résistance, surtout s'il est en fer).

• Il se produit un effet analogue en ce qui concerne la résistance, car à l'équilibre du pont sa résistance est égale à la partie réelle de l'impédance :

\displaystyle R_e=\frac{r}{(1-Lcω^2 )^2+(rcω)^2}+R

.

Ceci ne correspond plus à :

\displaystyle r=R.\left(\frac{V_A}{V_B} -1\right)

mais à :

\displaystyle \frac{V_A}{V_B} =\frac{R_e}{R}

\displaystyle r_{app}=R.\left(\frac{V_A}{V_B} -1\right)=\frac{r}{(1-Lcω^2 )^2+(rcω)^2}

.

• Avec :

\displaystyle λ=\frac{1}{r_{app} \,c^2 \,ω^2}

;

\displaystyle μ=\frac{1-Lcω^2}{c^2 \,ω^2}

l'équation s'écrit :

r^2-λ\:r+μ=0

et les solutions :

\displaystyle r=\frac{λ±\sqrt{λ^2-4μ}}{2}

.

On constate alors que dans la limite des basses fréquences

μ≈λ \;r_{app}

(à l'ordre le plus bas) et

R_e≈r+R

, ce qui donne après simplification :

\displaystyle r≈\frac{1}{r_{app} \:c^2 \,ω^2}

r≈r_{app}

.

La première expression est sans intérêt car elle tend vers l'infini. La solution correspondant à l'accord cherché est donc la seconde :

\displaystyle r=\frac{λ-\sqrt{λ^2-4μ}}{2}=\frac{1-\sqrt{1-4 \,r_{app}^{\:\:2}\;c^2 \,ω^2.(1-Lcω^2 )}}{2 \,r_{app} \:c^2 \,ω^2}

, qui redonne bien

r≈r_{app}

quand

c

est négligeable.

On obtient ainsi les variations suivantes (la courbe réelle est en fait plus ou moins différente, car la résistance n'est pas constante, mais le comportement limite est du même type ).

On constate que la résistance apparente augmente très nettement à l'approche de

\displaystyle ω≈\frac{1}{\sqrt{L\,c}}

. Il faut donc tenir compte de la capacité parasite pour celles des mesures qui (sans l'atteindre) s'approchent de la fréquence limite, afin de séparer cette augmentation apparente des variations réelles dues aux courants induits et à l'effet de peau (non décrits ici).

◊ remarque : une observation plus détaillée semble montrer que la perturbation intervient à des fréquences légèrement supérieures pour

r_{app}

que pour

L_{app}

(

≈5030 \:\mathrm{Hz}

au lieu de

4870 \:\mathrm{Hz}

dans l'exemple étudié).

2.2. Matériaux magnétiques et noyau de la bobine

• Lorsqu'ils sont soumis à un champ magnétique qui serait

B_0

en leur absence, certains matériaux deviennent aimantés et le champ total qui en résulte correspond à :

B=B_0 .(1+χ)

où

χ

est appelé “susceptibilité magnétique” du matériau.

• La classification des principales catégories de matériaux magnétiques s'effectue selon leur susceptibilité

χ

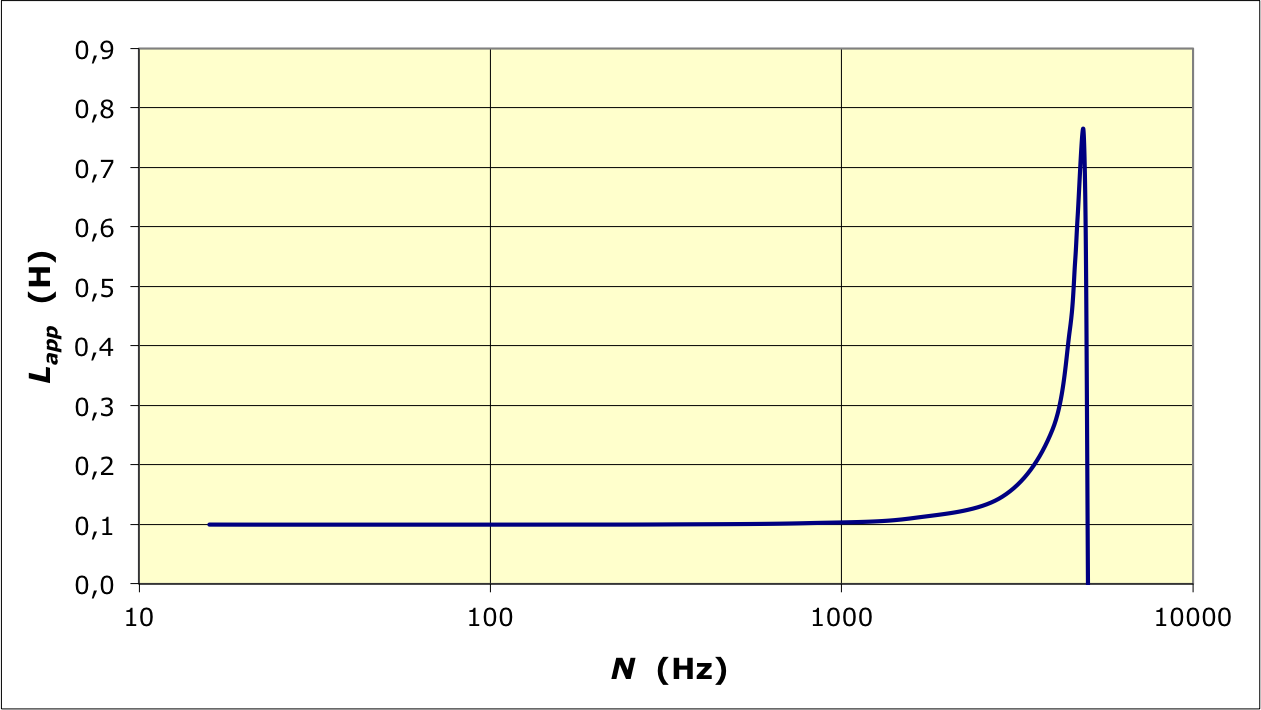
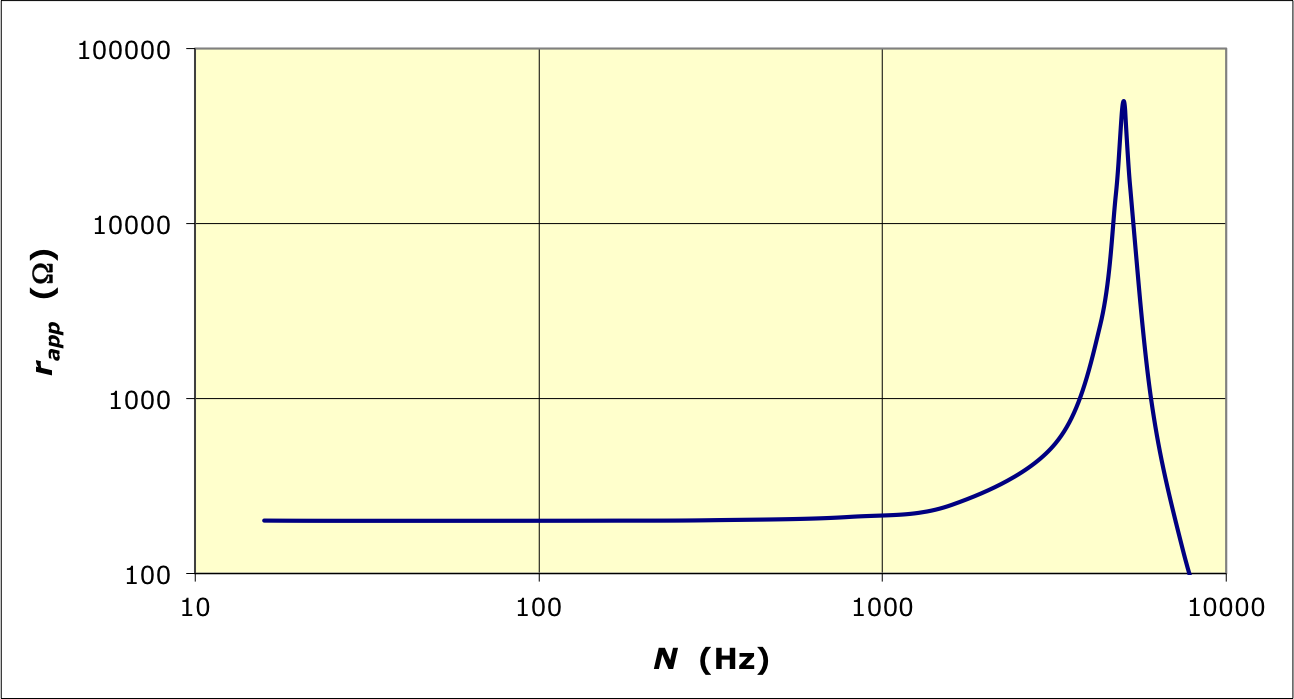
◊	les matériaux diamagnétiques (cuivre, argent, or, bismuth, béryllium) ont une susceptibilité faible et négative (environ $-{10}^{-5}$ ) ;
◊	les matériaux paramagnétiques (aluminium, platine, manganèse) ont une susceptibilité faible et positive (environ ${10}^{-3}$ à ${10}^{-5}$ ) ;
◊	les matériaux ferromagnétiques qui sont les plus importants (fer, cobalt, nickel, terres rares) ont une susceptibilité positive et forte ( $50$ à $10 \,000$ ) ; de plus, cette susceptibilité n'est pas constante (elle dépend non seulement du champ appliqué, mais aussi des champs auxquels le matériau a été soumis antérieurement ; effet d'aimantation persistante nommé “hystérésis”).

◊ remarque : dans un matériau diamagnétique, le champ magnétique subi modifie légèrement le mouvement des électrons dans les atomes, d'une façon qui tend à créer un faible champ magnétique de sens contraire ; le champ résultant est donc légèrement diminué.

◊ remarque : dans un matériau paramagnétique, chaque atome possède un moment magnétique (il se comporte comme un aimant) mais le désordre dû à l'agitation thermique fait que l'effet résultant est nul par compensation ; lorsqu'il subit un champ magnétique extérieur, les moments magnétiques tendent un peu à s'orienter dans le même sens et l'effet résultant est donc un peu augmenté.

◊ remarque : dans un matériau ferromagnétique, chaque atome possède un moment magnétique et les interactions entre eux (moins sensibles à l'agitation thermique) les fait s'aligner dans le même sens que leurs proches voisins : il se forme des domaines d'orientation commune ; la diversité des domaines fait que l'effet résultant est a priori nul, mais sous l'effet d'un champ extérieur subi les domaines se modifient et créent un champ résultant nettement plus grand (cette aimantation persiste après disparition du champ subi et ne s'atténue que progressivement sous l'effet de l'agitation thermique).

◊ remarque : il existe aussi des matériaux anti-ferromagnétiques (

\mathrm{MnO}

\mathrm{FeO}

...) ; chaque atome possède un moment magnétique et les interactions entre eux (moins sensibles à l'agitation thermique) les fait s'aligner dans le sens contraire à celui leurs proches voisins : l'effet résultant est a priori nul par compensation, mais sous l'effet d'un champ extérieur subi les compensations diminuent et cela crée un champ résultant un peu plus grand.

◊ remarque : il existe aussi des matériaux ferrimagnétiques (

\mathrm{NiFe_2 O_4}

...) ; assez semblables aux anti-ferromagnétiques mais avec deux sortes de moments magnétiques, dont l'alternance fait que les compensations ne sont jamais totales : ces matériaux ont une aimantation non nulle même en l'absence d'un champ extérieur subi.

2.3. Effet de peau

• Lorsque la fréquence

N

augmente, les signaux électriques se propagent dans le réseau comme des ondes électro-magnétiques à la vitesse de la lumière

c

; leur étude nécessite un raisonnement ondulatoire non évident. Quand la fréquence augmente, le courant ne circule plus qu'en surface des fils dans une épaisseur décroissante (

≈2 \:\mathrm{mm}

1 \:\mathrm{kHz}

pour le cuivre) ; ce phénomène, nommé “effet de peau” est proportionnel à

N^2

. Cela augmente la résistance en diminuant la “section utile” des fils.

2.4. Bobine sans noyau

• Le montage est réalisé avec une bobine d'inductance

L=\text{67,0}±\text{1,9} \:\mathrm{mH}

(mesurée avec un inductancemètre) et de résistance

r=\text{10,1}±\text{0,3} \:\mathrm{Ω}

(mesurée avec un ohm-mètre).

Les mesures par équilibre du pont montrent que jusqu'à environ

10 \:\mathrm{kHz}

l'inductance conserve cette valeur. Au delà, on constate une divergence due à la capacité parasite entre les spires, comme indiqué par la simulation précédente.

• De façon analogue, la résistance conserve à peu près la valeur mesurée initialement jusqu'à environ

1 \:\mathrm{kHz}

(à part une mesure douteuse vers

200 \:\mathrm{Hz}

) puis diverge au delà de

10 \:\mathrm{kHz}

, mais entre les deux on observe en outre une croissance comme

N^2

due à l'effet de peau.

2.5. Bobine avec noyau de Cu ou Al

• Les résultats obtenus sont quasi-identiques avec un noyau de

\mathrm{Cu}

\mathrm{Al}

; on présente ici le cas du cuivre.

• Le montage est réalisé avec une bobine d'inductance

L=\text{51,8}±\text{1,5} \:\mathrm{mH}

(mesurée avec un inductancemètre) et de résistance

r=\text{10,1}±\text{0,3} \:\mathrm{Ω}

(mesurée avec un ohm-mètre).

◊ remarque : il s'agit de la même bobine que celle étudiée précédemment sans noyau ; la valeur différente de

L

indique que l'inductance-mètre, qui mesure en régime transitoire avec

τ≈1 \:\mathrm{ms}

, est sensible à la présence du noyau d'une façon analogue au pont utilisé ici pour

N≈1 \:\mathrm{kHz}

• On constate un comportement globalement semblable à celui sans noyau (l'effet de son matériau diamagnétique est négligeable), si ce n'est que pour les fréquences intermédiaires l'inductance diminue d'autant plus que la fréquence augmente (la limite aux faibles fréquences est comparable à la valeur sans noyau).

Cela peut s'interpréter par les “courants de Foucault” : dans un noyau conducteur du courant, les variations du champ magnétique subi causent des courants induits qui tendent à créer un champ contraire, proportionnellement à la vitesse de variation. Le champ magnétique total est donc d'autant plus diminué qu'il varie vite.

• De façon analogue, on constate pour

r

un comportement globalement semblable à celui sans noyau (l'effet de son matériau diamagnétique est négligeable), mais pour les fréquences intermédiaires la résistance augmente d'autant plus que la fréquence augmente (la limite aux faibles fréquences est comparable à la valeur sans noyau).

Ici encore, cela peut s'interpréter par les “courants de Foucault” : les courants induits consomment de l'énergie par effet Joule ; cette énergie provient du champ magnétique associé au courant subi dans le circuit, de ce fait tout se passe comme si c'était ce courant qui avait plus d'effet Joule, donc avec une résistance plus grande pour la bobine. L'effet est d'autant plus important que le champ magnétique varie vite.

◊ remarque : si la résistance mesurée double ou triple par rapport à la limite des basses fréquences, cela signifie qu'il y a une ou deux fois plus de courants induits dans le noyau qu'il n'y en a dans la bobine (le noyau est en cuivre, comme la bobine) ; l'effet évolue moins vite que

N^2

car les courants restent induits dans l'ensemble du noyau (augmentation de

r

proportionnelle à

N

2.6. Bobine avec noyau de Fe feuilleté

◊ rappel : le “fer feuilleté” est constitué d'un assemblage de fines plaques de fer enduites de vernis (isolant) qui empêche les courants de Foucault de circuler d'une plaque à l'autre parallèlement aux spires (le feuilletage est parallèle à l'axe) ; la faible épaisseur rend négligeables les courants induits dans chaque plaque.

• Le montage est réalisé avec une bobine d'inductance

L=988±27 \:\mathrm{mH}

(mesurée avec un inductancemètre) et de résistance

r=\text{10,2}±\text{0,3} \:\mathrm{Ω}

(mesurée avec un ohm-mètre).

◊ remarque : il s'agit de la même bobine que celle étudiée précédemment sans noyau ; la valeur très supérieure de

L

est caractéristique du paramagnétisme du fer : les moments magnétiques des atomes amplifient le champ magnétique subi ; l'effet sur la résistance est négligeable car le noyau est feuilleté.

• On constate pour

L

un comportement globalement semblable à celui sans noyau (le fer feuilleté empêche les courants induits), mais le paramagnétisme du fer multiplie le champ magnétique (et donc

L

) par

≈15

.

• On constate pour

r

un comportement analogue à celui sans noyau (à part une mesure douteuse vers

30 \:\mathrm{Hz}

), mais aux fréquences intermédiaires

r

augmente avec la fréquence (la limite aux faibles fréquences est comparable à la valeur sans noyau). L'effet est plus important que celui avec courants de Foucault, pourtant absents dans ce cas ; cela est dû à l'énergie dépensée pour le retournement des moments magnétiques (l'hystérésis se comporte comme un frottement mécanique) et les conséquences sont analogues.