• La puissance instantanée reçue par
un dipôle est :
|
◊ remarque : la notation complexe est ici moins pratique car elle s'applique surtout aux opérations linéaires : .
◊ remarque : la notation complexe est ici moins pratique car elle s'applique surtout aux opérations linéaires : . |
|
| . |
| . |
| • Pour retrouver une expression analogue à
celle utilisée en régime continu, on définit les “valeurs
efficaces” :
et
. Ainsi on obtient : , où le coefficient “” est appelé “facteur de puissance” ; pour un dipôle linéaire : . |
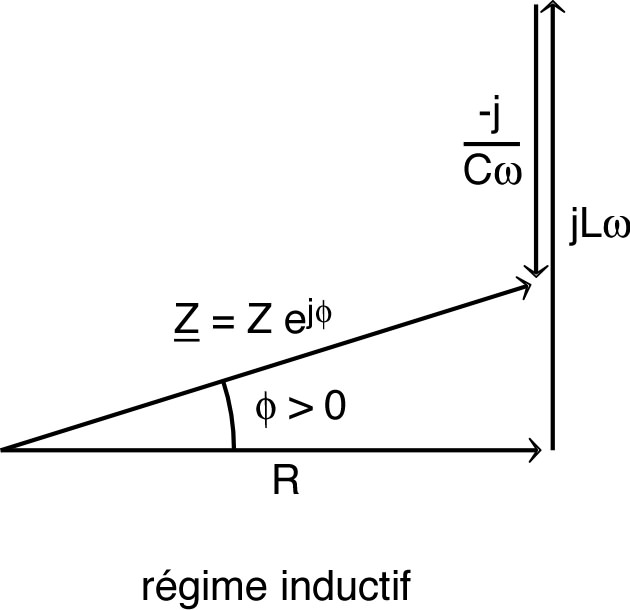
| ; ; |
| ◊ |
ce n'est pas un représentant de
,
puisque
; |
| ◊ |
ce n'est pas un représentant de , puisque ne représente pas les variations de . |
| Pour un générateur de f.e.m. efficace (référence des phases) et d'impédance , branché sur un “circuit utile” d'impédance , comment ajuster pour que la puissance reçue par soit maximum ? | 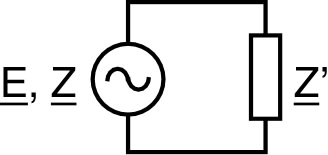 |
| , où . |

| , où . |
 |
 |
| ◊ |
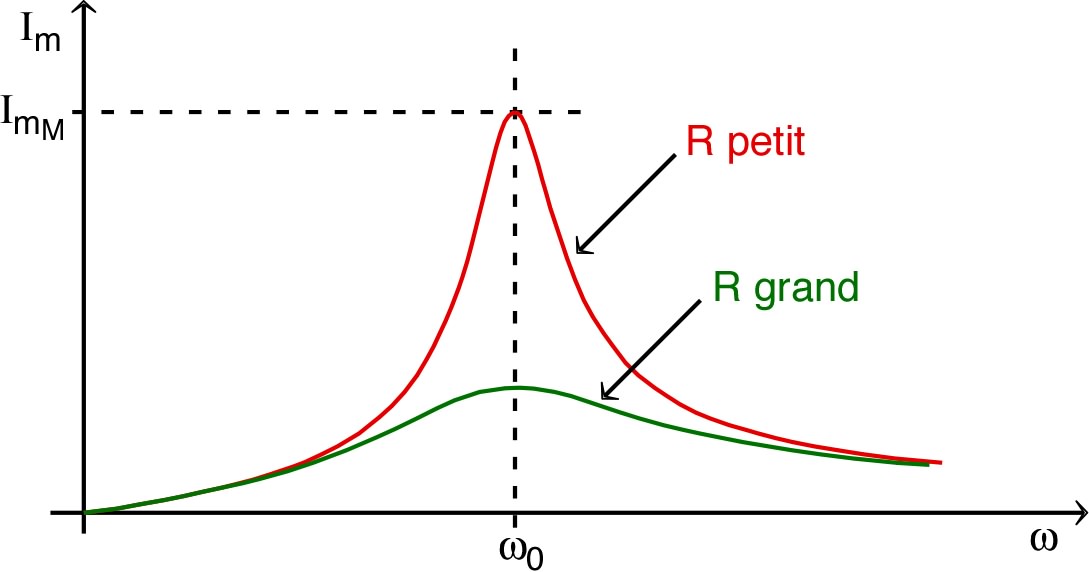
que la fréquence de résonance dépend de : elle est d'autant inférieure à la fréquence propre que la résistance est grande ; elle tend vers zéro pour une valeur “critique” (différente de celle des régimes transitoires) ; il n'y a pas de maximum pour ; |
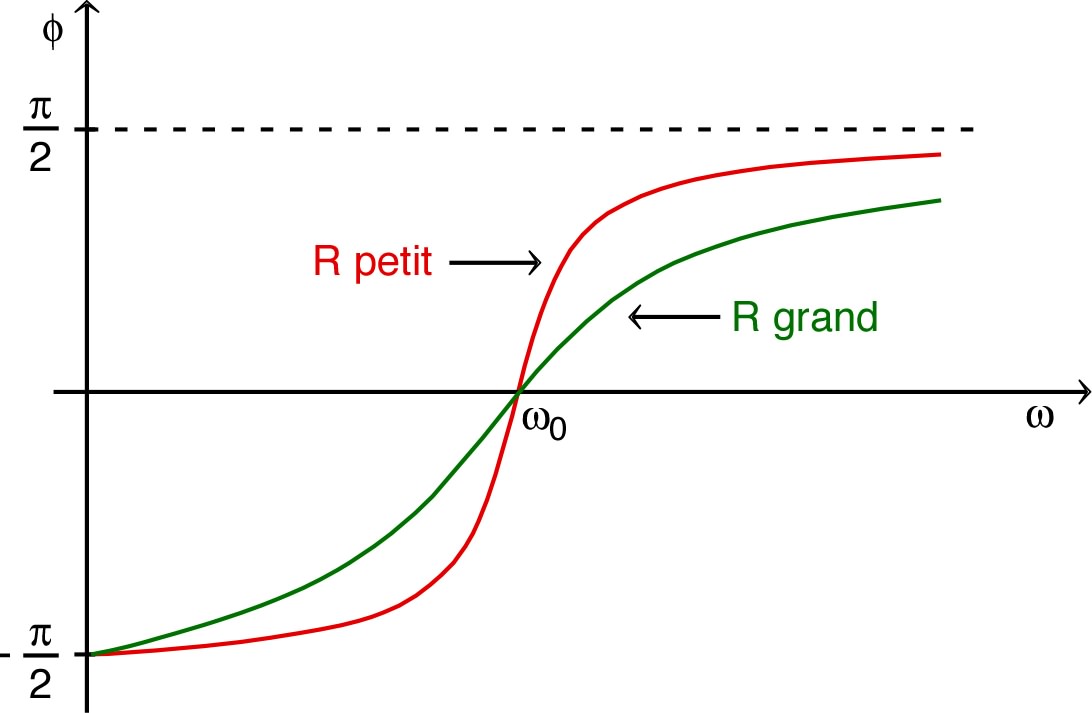
| ◊ |
que ne tend pas vers zéro mais vers quand la fréquence tend vers zéro ; le facteur de surtension (d'où son nom) est alors égal à . |