RÉGIME SINUSOÏDAL - ADAPTATIONS - corrigé des exercices

A. EXERCICES DE BASE

I. Amélioration du facteur de puissance

2.a.	• Le moteur équivaut à une impédance $\underline{Z}$ en série avec une f.c.e.m. $\underline{E}$ qui dépend du régime du moteur (inconnu) ; le mieux est de chercher un raisonnement général qui ne fasse aucune hypothèse sur ce régime.                                          • Les conditions nécessaires pour faire fonctionner le moteur ne dépendent que de sa structure interne ; pour obtenir un fonctionnement donné, il faut imposer les mêmes conditions avec ou sans adaptation.
2.b.	• Le facteur de puissance égal à $1$ correspond à un comportement purement résistif ; le courant est alors en phase avec la tension. • En prenant la tension comme référence des phases :  $\underline{u}=U_m \: \mathrm{e}^{\mathrm{j}ω\,t}$  et  $\underline{i}=I_m \: \mathrm{e}^{\mathrm{j}(ω\,t+ϕ)}$ .  On veut ajouter un condensateur en parallèle, de telle façon que, soumis à la même tension $\underline{u}$ et parcouru par un courant  $\underline{i}''=\mathrm{j} C\,ω \;\underline{u}$ ,  il donne un courant total  $\underline{i}'=\underline{i}+\underline{i}''=\mathrm{e}^{\mathrm{j}ω\,t} \: \left(I_m \: \mathrm{e}^{\mathrm{j}ϕ}+\mathrm{j} C\,ω \;U_m \right)$  en phase avec $\underline{u}$ . • On obtient donc :  $\mathrm{Im}\left(I_m \: \mathrm{e}^{\mathrm{j}ϕ}+\mathrm{j} C\,ω\; U_m \right)=I_m \; \sin(ϕ)+C\,ω \;U_m=0$  c’est-à-dire :  $\displaystyle C=-\frac{I \;\sin(ϕ)}{ω \:U}$  (en simplifiant par $\sqrt{2}$ ).  Ceci n'est donc possible que dans les cas où  $\sin(ϕ)<0$ ,  c’est-à-dire que le courant $\underline{i}$ doit être en retard par rapport à la tension $\underline{u}$ (mais un moteur électrique est normalement ainsi, à cause de l'inductance de ses bobinages électromagnétiques). • Finalement :  $\displaystyle C=\frac{I \:\sqrt{1-\cos^2(ϕ)}}{ω \:U}=113 \:\mathrm{μF}$ . ◊ remarque :  il n’était pas du tout évident a priori que le choix de $C$ soit possible indépendamment du régime de fonctionnement du moteur.
2.c.	• Dans ces conditions (partie imaginaire nulle) : $I'=\left|\underline{I}'\right|=\left|I \: \mathrm{e}^{\mathrm{j}ϕ}+\mathrm{j} C\,ω \:U \right|=\mathrm{Re}\left(I\: \mathrm{e}^{\mathrm{j}ϕ}+\mathrm{j} C\,ω \:U \right)=I \: \cos(ϕ)=\text{9,1} \:\mathrm{A}$ . ◊ remarque : la puissance consommée par le moteur est alors la même :  $P=U \:I'=U \:I \: \cos(ϕ)$ ,  mais obtenue avec  $I'<I$  ;  il y a moins de pertes dans les lignes de transport, car le condensateur absorbe de l’énergie pendant une partie de la période où le moteur n’est pas à même de l’absorber, puis la restitue au bon moment (en moyenne, le condensateur ne consomme pas d’énergie).

II. Bande passante ; facteur de qualité

1.

• L'impédance complexe est :  $\displaystyle \underline{Z}_0=R+\mathrm{j} \:\left(L \,ω-\frac{1}{C \,ω}\right)=R+\mathrm{j} \:S$ . • La partie imaginaire $S$ est nulle à la résonance  ($\displaystyle ω=ω_0=\frac{1}{\sqrt{L \:C}}$ ),  elle tend vers $-∞$ quand  $ω→0$  et elle tend vers $+∞$ quand  $ω→∞$ . • Par suite, le lieu de $\underline{Z}_0$ est la droite d'abscisse $R$ (parallèle à l'axe imaginaire). • En suivant l'indication de l'énoncé :  $\displaystyle \left|\frac{1}{\underline{Z}_0} -\frac{1}{2 \,R}\right|=\left|\frac{2 \,R-(R+\mathrm{j} \:S)}{2 \,R.(R+\mathrm{j} \:S)}\right|=\frac{1}{2 \,R} \: \left|\frac{R-\mathrm{j} \:S}{R+\mathrm{j} \:S}\right|=\frac{1}{2 \,R}$ . • Par suite, le lieu de $\displaystyle \frac{1}{\underline{Z}_0}$ est le cercle centré sur l'axe réel à l'abscisse $\displaystyle \frac{1}{2 \,R}$ et de rayon $\displaystyle \frac{1}{2 \,R}$ . ◊ remarque : les propriétés  $\displaystyle \left|\frac{1}{\underline{Z}_0} \right|=\frac{1}{|\,\underline{Z}_0 |}$   et   $\displaystyle \arg\left(\frac{1}{\underline{Z}_0} \right)=-\arg\left(\underline{Z}_0\right)$  peuvent être associées à deux transformations ponctuelles dans le plan complexe : une inversion (de pôle $O$ et de puissance $1$) suivie d'une symétrie (par rapport à l'axe réel) ; l'inversion transforme la droite précédente en un cercle qui est invariant pour la symétrie, d'où la conclusion (si on connaît les propriétés de l'inversion).

2.

• Graphiquement, les points représentatifs sont tels que  $\displaystyle OM=\frac{1}{R \:\sqrt{2}}$ ,  ce qui correspond à des triangles rectangles isocèles inscrits dans un demi-cercle. • Il y a deux tels points, $M$ et $M'$, qui correspondent à :  $\arg\left(\underline{Z}_0\right)=±\frac{π}{4}$  et donc :  $\displaystyle L \,ω-\frac{1}{C \,ω}=±R$ . • En notant  $\displaystyle λ=\frac{R}{2 \,L}$  les solution positives de ces deux équations sont : $ω_1=-λ+\sqrt{λ^2+ω_0^{\:2}}$  (au point $M$) ; $ω_2=+λ+\sqrt{λ^2+ω_0^{\:2}}$  (au point $M'$).

B. EXERCICE D’APPROFONDISSEMENT

III. Ondemètre

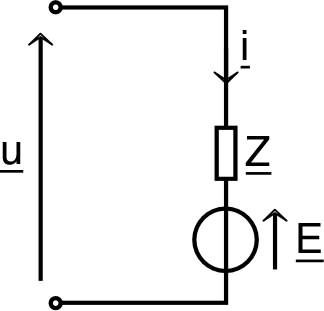
• La tension aux bornes de la bobine peut s'écrire (si on néglige sa résistance) :  $\displaystyle u=-\frac{dΦ}{dt}$  où $Φ$ est le flux magnétique total dans la bobine :  $Φ=Φ_{ext}+Φ_{auto}$  avec  $Φ_{auto}=L \:i$  (flux induit dans la bobine par son propre champ). Ceci donne donc :  $\displaystyle u=-\frac{dΦ_{ext}}{dt}-L \: \frac{di}{dt}$ . • Mais on peut écrire  $\displaystyle u=\frac{q}{C''}$  avec  $\displaystyle i=\frac{dq}{dt}$  en posant  $C''=C$  ou  $C''=C+C'$  selon le cas ; par suite, la réponse du circuit correspond à la solution de l'équation :  $\displaystyle L \:\ddot{q}+\frac{q}{C''}=- ω \:Φ_m \: \cos(ω \:t)=e(t)$  qui décrit un circuit $LC''$ soumis à $e(t)$ sinusoïdale. • Ce modèle est simplifié : il néglige la résistance sans donner aucune indication des conditions initiales... or, en l'absence de résistance, le régime “transitoire” (à la pulsation  $\displaystyle ω_0=\frac{1}{\sqrt{L \:C''}}$  ) n'est pas amorti, donc il garde en permanence une importance aussi grande que le régime “sinusoïdal permanent” (à la pulsation  $ω≠ω_0$ ). • En fait, la résistance n'est jamais nulle (il y a au moins quelques $\mathrm{ohms}$ pour la bobine) : on réduit cette résistance le plus possible afin de rendre le dispositif plus sensible au champ extérieur, mais il faut conserver une résistance minimum pour que le régime transitoire soit amorti assez vite pour permettre des mesures dans des délais raisonnables. 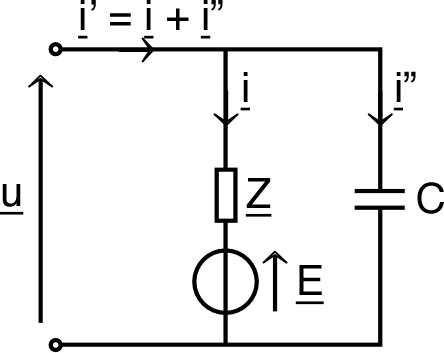• L'impédance (complexe) du circuit $LC''$ est :  $\displaystyle \underline{Z}=\mathrm{j} \:\left(L \,ω-\frac{1}{C'' \,ω}\right)$  et le courant est donc :  $\displaystyle \underline{I}=\frac{\underline{E}}{\underline{Z}}$  ;  la tension aux bornes du condensateur est alors :  $\displaystyle \underline{U}=\frac{1}{\mathrm{j} C'' ω} \: \underline{I}=\frac{1}{\mathrm{j} C'' ω} \, \frac{\underline{E}}{\underline{Z}}=\frac{\underline{E}}{1-L\,C'' ω^2}$  (en ne considérant que le régime permanent). • Cette relation est valable en valeurs “maximum” ou “efficaces” complexes ; les multimètres mesurent les valeurs efficaces (réelles), qui correspondent aux modules des représentants complexes :  $\displaystyle U=\frac{E}{\left|1-L\,C'' ω^2 \right|}$ . ◊ remarque : la quantité $(1-L\,C'' ω^2 )$ est réelle, mais son signe correspond à l'argument du représentant complexe et il doit être mis à part. 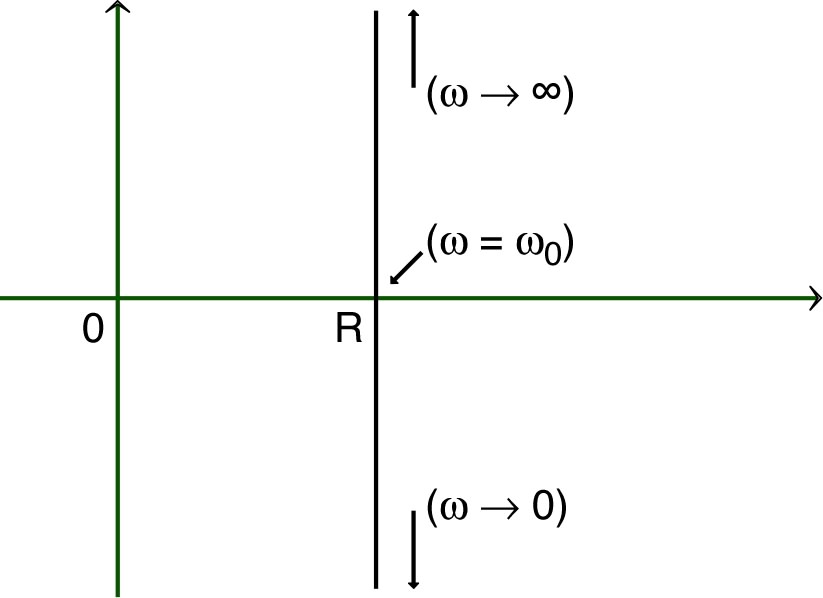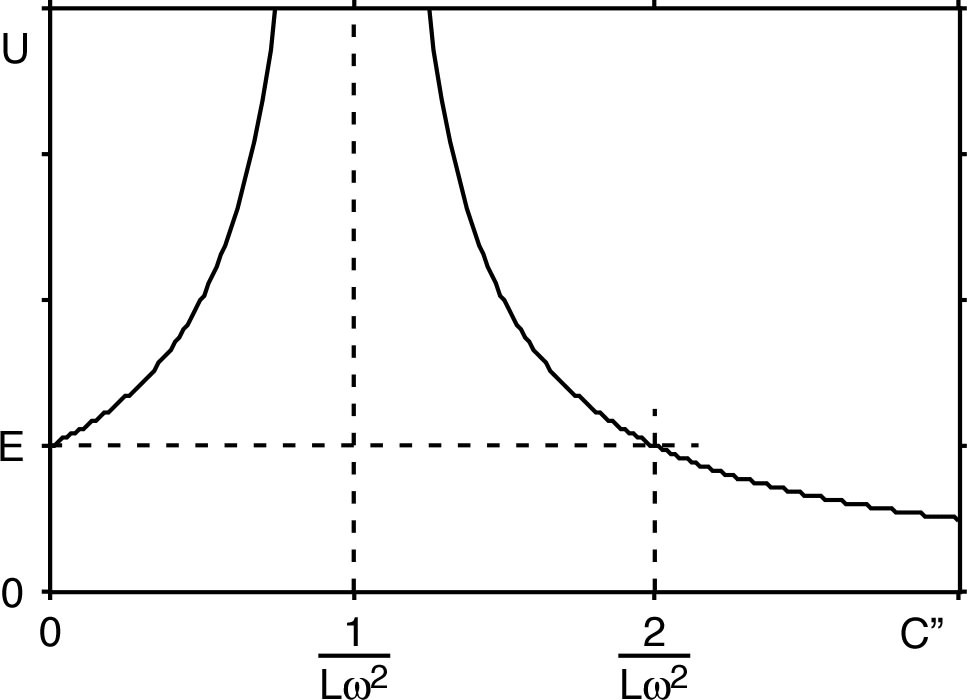• Cette relation décrit une résonance “infiniment” aiguë, compte tenu du fait qu'on a négligé la résistance du circuit (et en particulier celle de la bobine) ; cette courbe de résonance peut être tracée, pour $ω$ fixé, en fonction de $C''$. ◊ remarque : c'est “l'absence” de résistance qui donne une résonance tendant vers l'infini ; ceci montre l'intérêt d'une résistance faible : ◊ d'une part le maximum est d'autant plus grand, donc le dispositif “amplifie” l'onde reçue et est plus sensible en amplitude ; ◊ d'autre part la courbe est d'autant plus “aiguë” et, compte tenu des pentes plus grandes, le dispositif est plus sensible aux réglages de $C$. 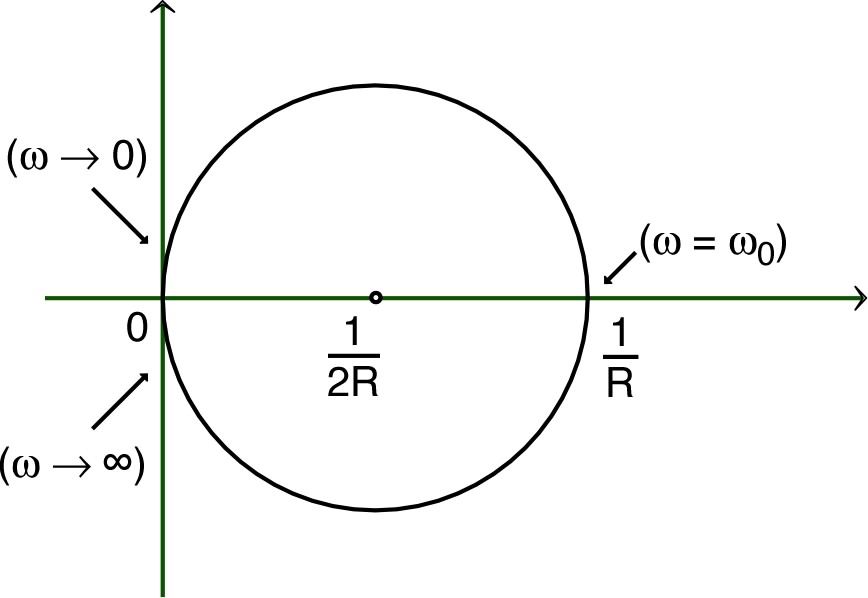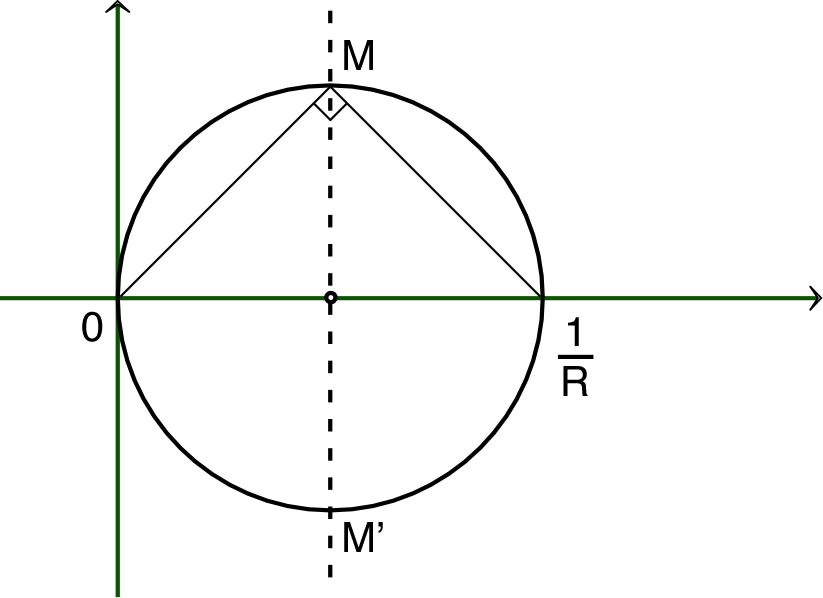• On constate que pour toute valeur  $\displaystyle C''<\frac{2}{L \,ω^2}$  on peut trouver une autre valeur de capacité (symétrique par rapport à $\displaystyle \frac{1}{L \,ω^2}$ ) donnant la même tension $U$ pour $ω$ fixé. • Pour le circuit étudié, ceci correspond à chercher la condition (sur $ω$) pour que les capacités $C$ et $C+C'$ (imposées) soient ainsi conjuguées, c'est-à-dire :  $\left|1-L \,C \,ω^2 \right|=\left|1-L .(C+C') \, ω^2 \right|$ .  D'après le graphique, il est clair que dans ce cas les deux capacités correspondent à des signes contraire de  $(1-L\,C'' ω^2 )$  ;  l'équation à résoudre est donc :  $1-L \,C \,ω^2=-1+L .(C+C') \, ω^2$  d'où on déduit :  $\displaystyle ω=\frac{1}{\sqrt{L.\left(C+\frac{C'}{2}\right)}}$ .