RÉGIME SINUSOÏDAL - ADAPTATIONS - exercices


A. EXERCICES DE BASE

I. Amélioration du facteur de puissance

1.     • Un moteur électrique est alimenté en régime sinusoïdal de fréquence 50Hz50 \:\mathrm{Hz} , de courant efficace  I=12AI=12 \:\mathrm{A} ,  sous une tension efficace  U=220VU=220 \:\mathrm{V}  ;  sa puissance est  P=2,0kWP=\text{2,0} \:\mathrm{kW} .
        • Quel est le facteur de puissance  cos⁡(ϕ)\cos⁡(ϕ)  de cet appareil ?

2.     • Afin d'améliorer le facteur de puissance, on se propose de placer une capacité CC en parallèle aux bornes du moteur.
        a) Justifier que cette adaptation impose que la tension imposée et le courant dans le moteur soient inchangés.

sinAdapt_ex_Im/sinAdapt_ex_Im1.jpg
 sinAdapt_ex_Im/sinAdapt_ex_Im2.jpg


        b) Montrer qu'une telle adaptation est possible et permet d'obtenir pour l'ensemble un facteur de puissance égal à 11 .
        ◊ indication : le moteur équivaut à une impédance Z_\underline{Z} en série avec une f.c.e.m. E_\underline{E} qui dépend de son régime ; le mieux est de chercher un raisonnement général qui ne fasse aucune hypothèse ni sur Z_\underline{Z} ni sur E_\underline{E} .

        c) Quelle est alors le courant efficace I′I' fourni par le réseau d'alimentation ?

II. Bande passante ; facteur de qualité

        • On associe en série une bobine (de résistance  R=10ΩR=10 \:\mathrm{Ω}  et d'inductance  L=0,10HL=\text{0,10} \:\mathrm{H} )  et un condensateur (de capacité  C=0,10μFC=\text{0,10} \:\mathrm{μF} ).  On note Z_0\underline{Z}_0 l'impédance complexe de ce circuit. On établit entre ses bornes AA et BB une tension uABu_{AB} sinusoïdale de pulsation ωω .

1.     • Représenter dans le plan complexe le lieu de Z_0\underline{Z}_0 ,  puis celui de 1Z_0\displaystyle \frac{1}{\underline{Z}_0} ,  lorsque ωω varie.
        ◊ indication : on peut montrer que  1Z_0−12R\displaystyle \frac{1}{\underline{Z}_0} -\frac{1}{2 \,R}  est un nombre complexe de module constant.

2.     • En utilisant la représentation précédente, calculer les valeurs ω1ω_1 et ω2ω_2 pour lesquelles  |Z_0|=R2\left|\,\underline{Z}_0 \right|=R \:\sqrt{2} .

3.     • Calculer en fonction de RR, LL et CC le facteur de qualité  Q=ω0∆ω\displaystyle Q=\frac{ω_0}{∆ω}  où  ω0=1LC\displaystyle ω_0=\frac{1}{\sqrt{L \:C}}   et   ∆ω=|ω2−ω1|∆ω=|ω_2-ω_1 |  ;  calculer numériquement ces quantités.



B. EXERCICE D’APPROFONDISSEMENT

III. Ondemètre

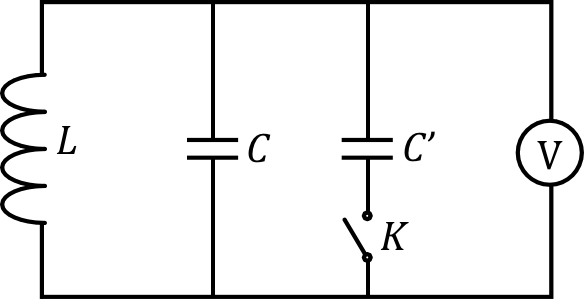
        • Pour mesurer la fréquence νν d'un champ magnétique oscillant, on peut utiliser un dispositif du type ci-contre, muni d'un voltmètre d'impédance quasi-infinie en mode alternatif.
        • Le flux du champ magnétique étudié à travers la bobine d'inductance LL est :  Φext=Φmsin⁡(ωt)Φ_{ext}=Φ_m \: \sin⁡(ω \,t) ,  avec  ω=2πνω=2π \:ν .
        ◊ indication : la force-électromotrice induite dans la bobine peut s’écrire :  e=−dΦdt\displaystyle e=-\frac{dΦ}{dt}  où  Φ=Φext+ΦautoΦ=Φ_{ext}+Φ_{auto}  est le flux magnétique total dans la bobine (avec  Φauto=LiΦ_{auto}=L \:i ).
 sinAdapt_ex_Im/sinAdapt_ex_Im3.jpg
        • On ajuste alors la capacité CC de telle façon que le voltmètre indique la même valeur quelle que soit la position de l'interrupteur. Montrer que dans ces conditions :  ω=1L.(C+C′2)\displaystyle ω=\frac{1}{\sqrt{L.\left(C+\frac{C'}{2}\right)}} .