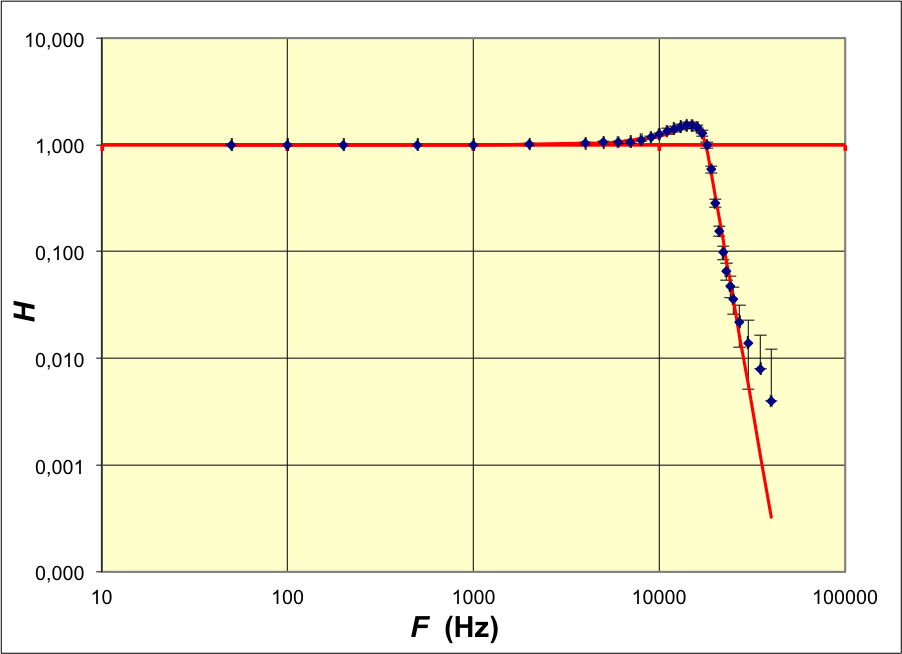
• Initialement, avec , on obtient : .
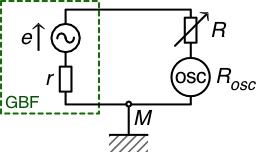
| • La résistance du générateur est
négligeable en comparaison de celle de l'oscilloscope
(inférieure aux incertitudes de mesure). Avec une
résistance
, le principe du pont diviseur de tension permet de
calculer :
. • Initialement, avec , on obtient : . |
 |
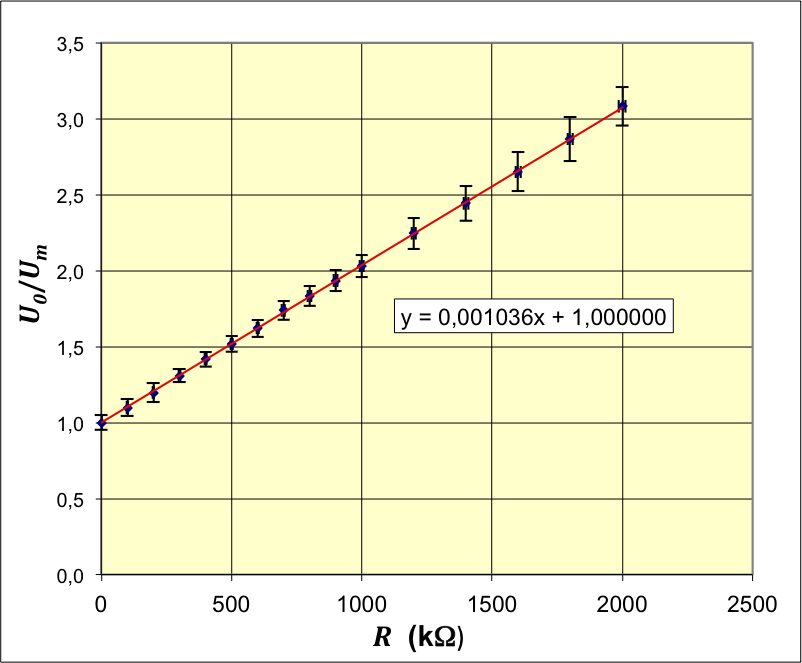
| ; . |
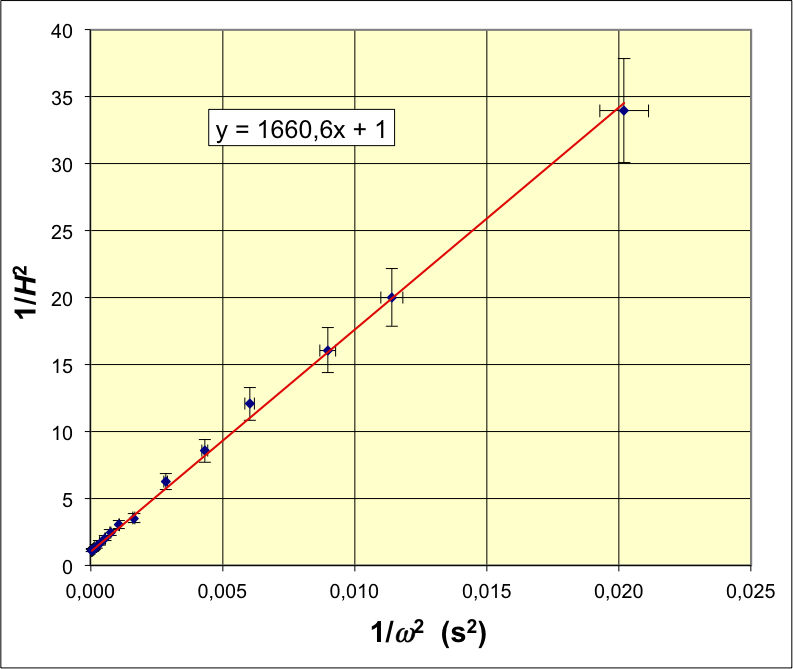
| ; . |
 |
 |