EC.VIII - RÉGIME SINUSOÏDAL

EC.VIII - RÉGIME SINUSOÏDAL - QUADRIPÔLES

1. Conventions de notation

• Un quadripôle électrocinétique est une portion de circuit reliée au “reste” du réseau par quatre bornes de branchement :

◊ remarque : comme pour les dipôles, les quadripôles sont respectivement “actifs” ou “passifs” selon qu’ils comportent ou non une source d'énergie.

• On définit les conventions de notation en se limitant aux cas usuels avec :

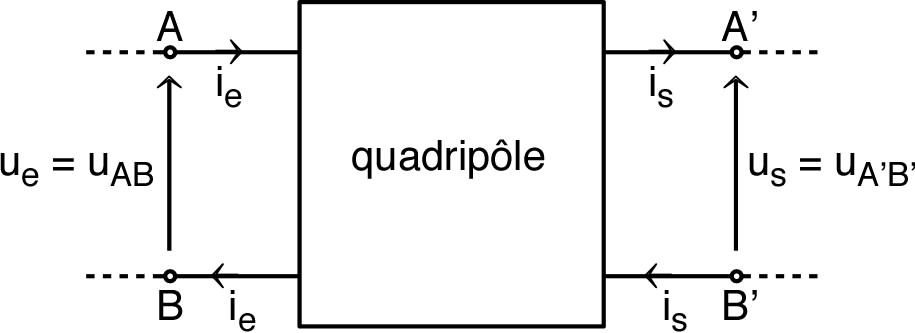
◊	deux “bornes d’entrée” (reliées à un dipôle générateur) par où passe un même “courant d’entrée” $i_e$ ;
◊	deux “bornes de sortie” (reliées à un dipôle récepteur) par où passe un même “courant de sortie” $i_s$ .

2. Caractéristiques d’entrée et de sortie

2.1. Définitions

• Pour le circuit branché en entrée, le quadripôle est décrit par une caractéristique dipolaire affine (éventuellement linéarisée) :

\underline{u}_e=\underline{e}_e+\underline{Z}_e \: \underline{i}_e

où

\underline{e}_e

est la f.e.m. d’entrée et où

\underline{Z}_e

est l'impédance d’entrée (notations complexes).

☞ remarque : les grandeurs

\underline{e}_e

\underline{Z}_e

dépendent en général de ce qui est branché en sortie du quadripôle.

• De même, pour le circuit branché en sortie, le quadripôle est décrit par une caractéristique affine (éventuellement linéarisée) :

\underline{u}_s=\underline{e}_s-\underline{Z}_s \: \underline{i}_s

où

\underline{e}_s

est la f.e.m. de sortie et où

\underline{Z}_s

est l'impédance de sortie.

☞ remarque : les grandeurs

\underline{e}_s

\underline{Z}_s

dépendent en général de ce qui est branché en entrée du quadripôle.

2.2. Exemple d’un circuit “RC”

• Soit un circuit “RC”, alimenté en entrée par un générateur de résistance

r

et avec en sortie, aux bornes du condensateur, une résistance (charge)

R_c

Les lois d’association des dipôles donnent alors :

\underline{u}_e=\underline{Z}_e \: \underline{i}_e

avec :

\displaystyle \underline{Z}_e=R+\frac{R_c \: \underline{Z}_C}{R_c+\underline{Z}_C}=R+\frac{R_c}{1+\mathrm{j} \,R_c \: Cω}

\underline{e}_e=0

• On peut de même étudier la caractéristique de sortie en utilisant les équivalences Thévenin-Norton (ou le théorème de Thévenin et la loi de Millman...).

On obtient ainsi :

\underline{u}_s=\underline{e}_s-\underline{Z}_s \: \underline{i}_s

avec :

\displaystyle \underline{e}_s=\frac{\underline{e}}{1+\mathrm{j} \,(R+r) \:Cω}

\displaystyle \underline{Z}_s=\frac{R+r}{1+\mathrm{j} \,(R+r) \:Cω}

📖 exercices n° I et II.

3. Fonctions de transfert

3.1. Définitions

• Pour caractériser un quadripôle, on utilise en outre des relations entre les grandeurs de sortie et les grandeurs d'entrée.

À partir de :

\underline{u}_e=\underline{U}_{em} \; \mathrm{e}^{\mathrm{j}ωt}

;

\underline{i}_e=\underline{I}_{em} \; \mathrm{e}^{\mathrm{j}ωt}

;

\underline{u}_s=\underline{U}_{sm} \; \mathrm{e}^{\mathrm{j}ωt}

;

\underline{i}_s=\underline{I}_{sm} \; \mathrm{e}^{\mathrm{j}ωt}

; on définit les “fonctions de transfert” (usuellement notées

\underline{H}(ω)=H(ω) \;\mathrm{e}^{\mathrm{j}ϕ(ω)}

) :

◊	les gains (complexes) en tension : $\displaystyle \frac{\underline{U}_s}{\underline{U}_e}$ et en courant : $\displaystyle \frac{\underline{I}_s}{\underline{I}_e}$ ;
◊	la transadmittance : $\displaystyle \frac{\underline{I}_s}{\underline{U}_e}$ et la transimpédance : $\displaystyle \frac{\underline{U}_s}{\underline{I}_e}$ .

☞ remarque : en général, les fonctions de transfert dépendent des circuits auxquels est relié le quadripôle en entrée et en sortie !

◊ remarque : on peut utiliser les valeurs complexes efficaces, maximum ou instantanées (mais de même type au numérateur et au dénominateur).

3.2. Notations en décibels

• Le gain complexe

\underline{H}(ω)

peut être décrit par

H(ω)

ϕ(ω)

; les courbes correspondantes sont appelées “diagrammes de Bode”.

La pulsation

ω

et le gain réel

H(ω)

peuvent varier dans des proportions considérables, donc on utilise des échelles logarithmiques (comme pour le

\mathrm{pH}

).

• D'une façon générale, on définit “l'unité

\mathrm{bel}

” (symbole

\mathrm{B}

) pour représenter une “unité de logarithme décimal” pour la puissance d’un signal.

De façon générale, la puissance est proportionnelle au carré de l’amplitude du signal, donc un gain d'un facteur

{10}^n

en tension (ou en courant) correspond à un gain

{10}^{2n}

en puissance ; ainsi une amplification d'un facteur

G={10}^3

en tension correspond à un “gain en

\mathrm{bels}

” :

G_{\mathrm{B}}=\log(G^2)=2 \, \log(G)=6 \,\mathrm{B}

.

On a ensuite pris l'habitude de compter en

\mathrm{décibels}

(symbole

\mathrm{dB}

) :

G_{\mathrm{dB}}=10 \: \log(G^2)=20 \: \log(G)

;

ainsi une amplification d'un facteur

G={10}^3

correspond à :

G_{\mathrm{dB}}=60 \:\mathrm{dB}

.

◊ remarque : il faut faire attention à la manipulation des signes :

◊	un gain $\underline{H}(ω)=-10$ correspond à $H_{\mathrm{dB}}=20 \:\mathrm{dB}$ et $ϕ=π$ (le signe négatif ne peut pas être pris en compte ainsi dans le logarithme) ;
◊	au contraire, un gain $\underline{H}(ω)=\text{0,1}$ donne $H_{\mathrm{dB}}=-20 \:\mathrm{dB}$ et $ϕ=0$ (le logarithme est négatif si $H(ω)<1$ ).

• Pour les fréquences, on utilise l'expression “décade” pour nommer une variation d'un facteur 10 , correspondant à une unité du logarithme décimal.

◊ remarque : une “octave” (variation d'un facteur 2 , utilisée pour la musique) correspond à

≈\,\text{0,3}

décade.

◊ remarque : si l'abscisse affiche le logarithme, l'homogénéité des unités fait qu'on doit utiliser

\displaystyle \log\left(\frac{ω}{ω_0}\right)

, avec une pulsation de référence

ω_0

arbitraire.

3.3. Exemple du circuit “RC”

3.3.1 Sens “intégrateur” ; filtre “passe bas”

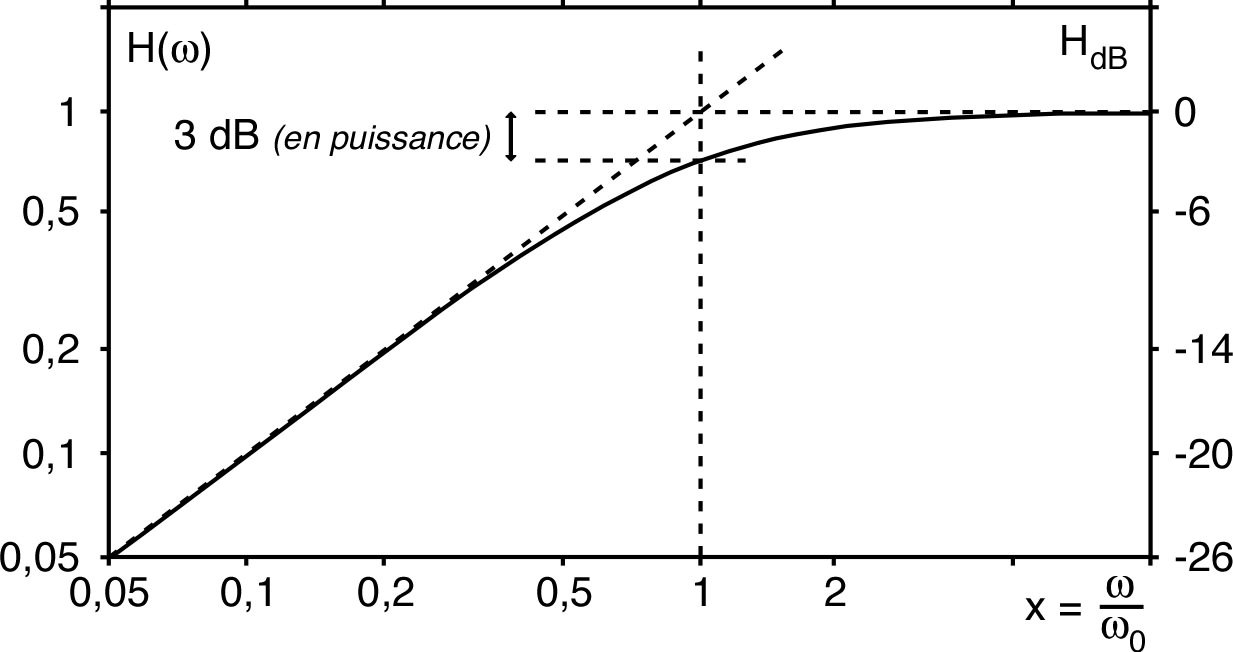
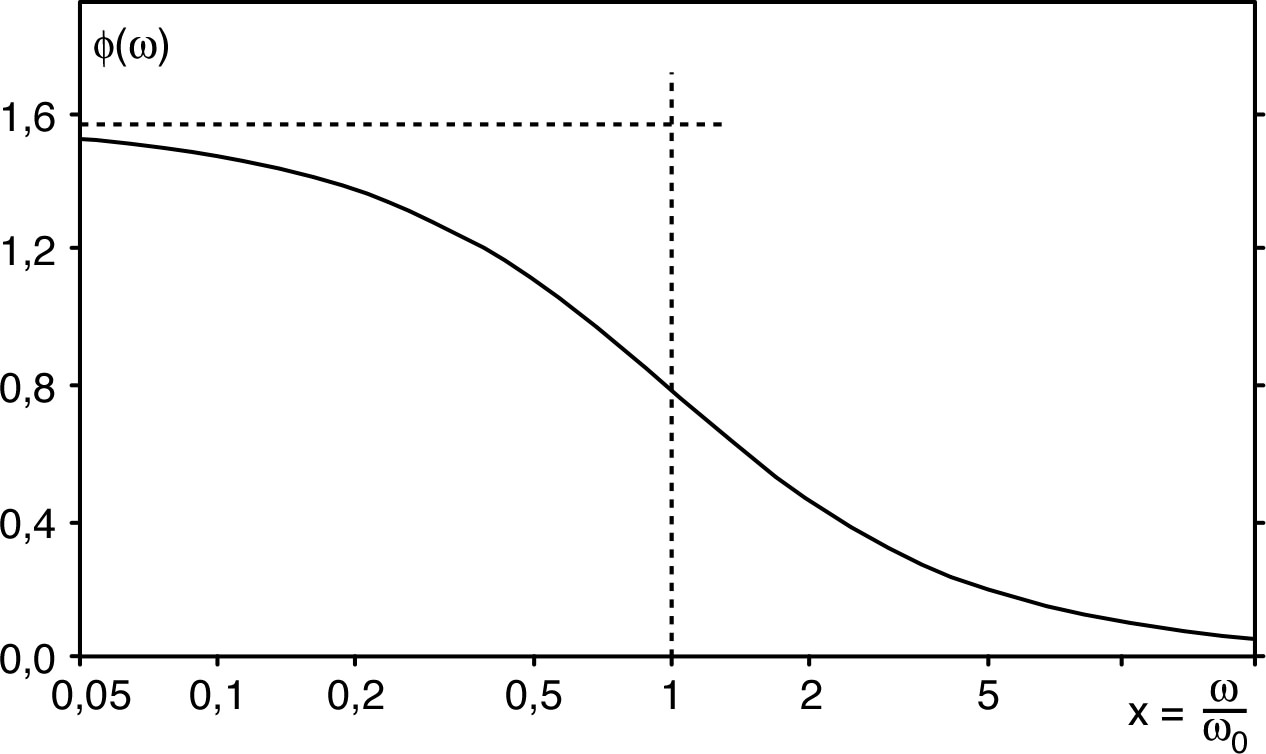
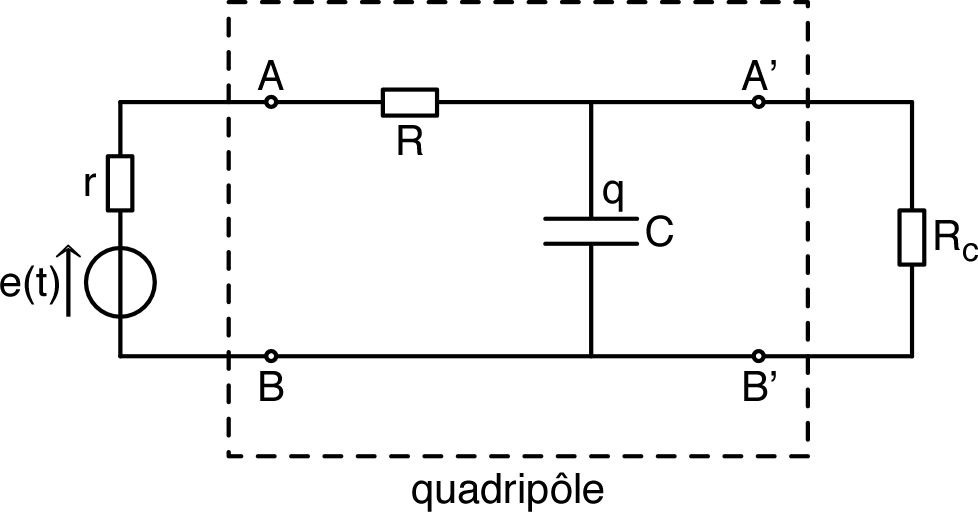
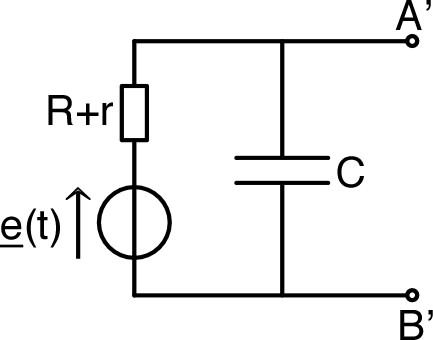
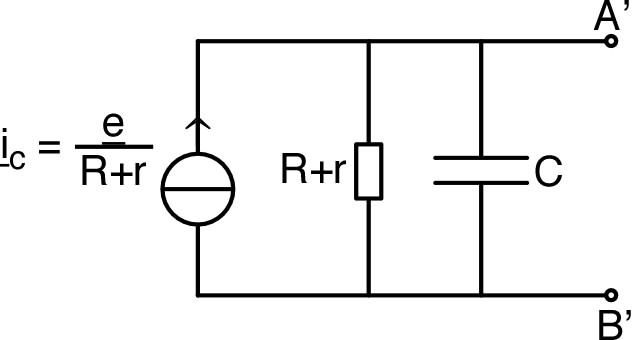
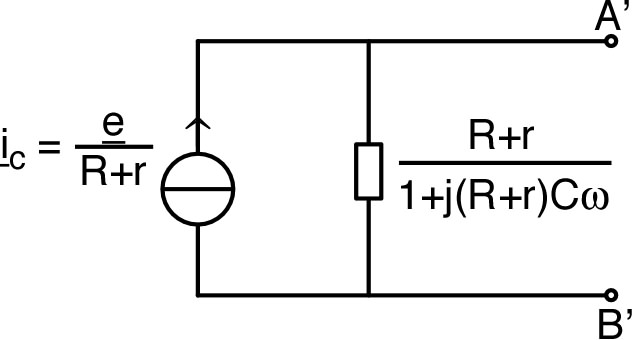
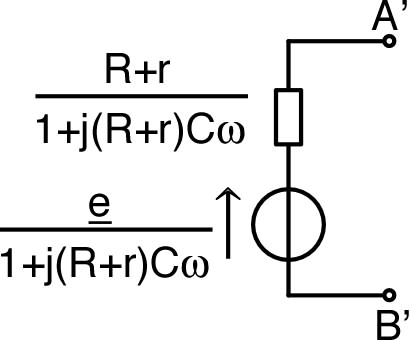
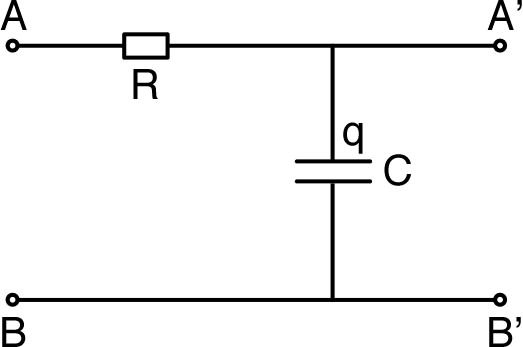
• On considère un circuit “RC” avec en sortie, aux bornes du condensateur, une charge “infinie” (sans effet puisque

\underline{i}_s≈0

).

Le courant est le même dans R et C, donc :

\displaystyle \underline{H}(ω)=\frac{\underline{U}_s}{\underline{U}_e} =\frac{\underline{Z}_C}{R+\underline{Z}_C}=\frac{1}{1+\mathrm{j} \,RCω}

Ce montage est “suiveur” à basse fréquence et “intégrateur” à haute fréquence :

\displaystyle \underline{H}(ω)≈\frac{1}{\mathrm{j} \,RCω}

\displaystyle ω≫ω_0=\frac{1}{RC}

(l'intégration divise par

\mathrm{j} \,ω

).

• On obtient pour

H(ω)

le diagramme suivant :

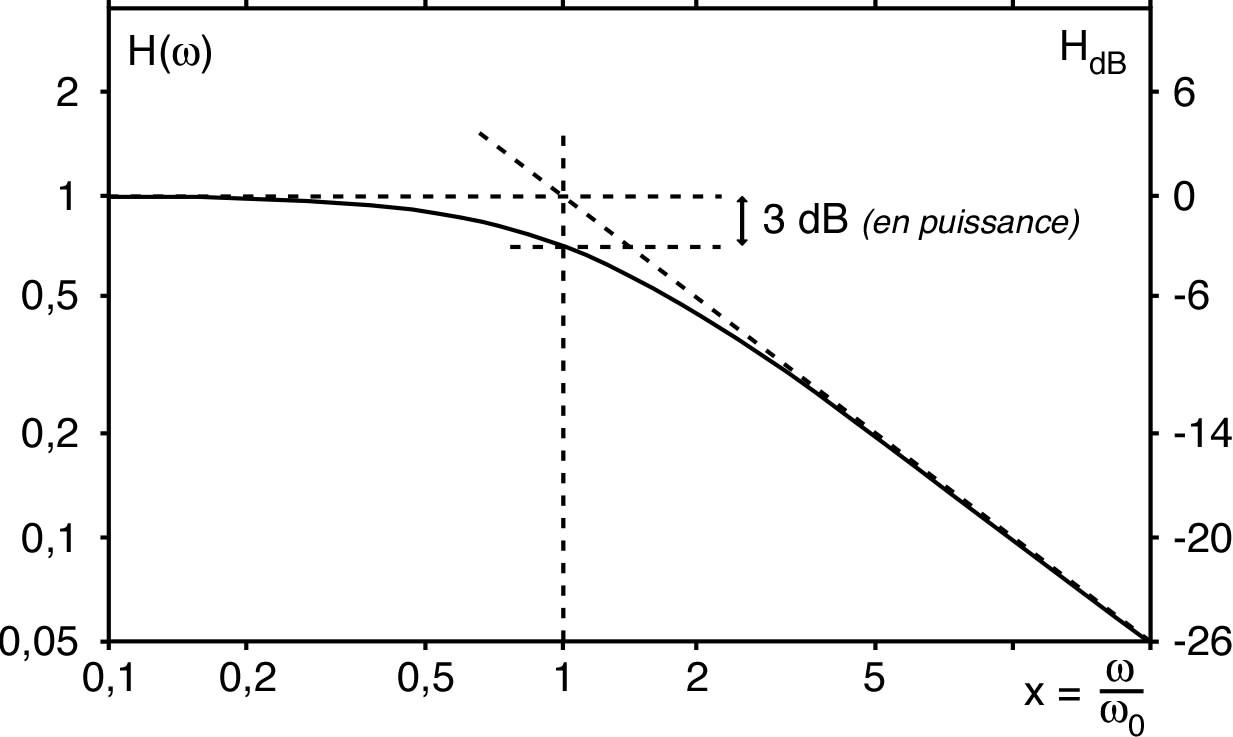
• L'ensemble des fréquences (ou des pulsations) pour lesquelles

\displaystyle H≥\frac{H_{max}}{\sqrt{2}}

est appelé “bande passante”.

Dans ce cas particulier, il n'y a qu'une “coupure supérieure” pour

ω=ω_0

.

• On obtient également pour le déphasage :

\displaystyle ϕ=- \arctan\left(\frac{ω}{ω_0}\right)

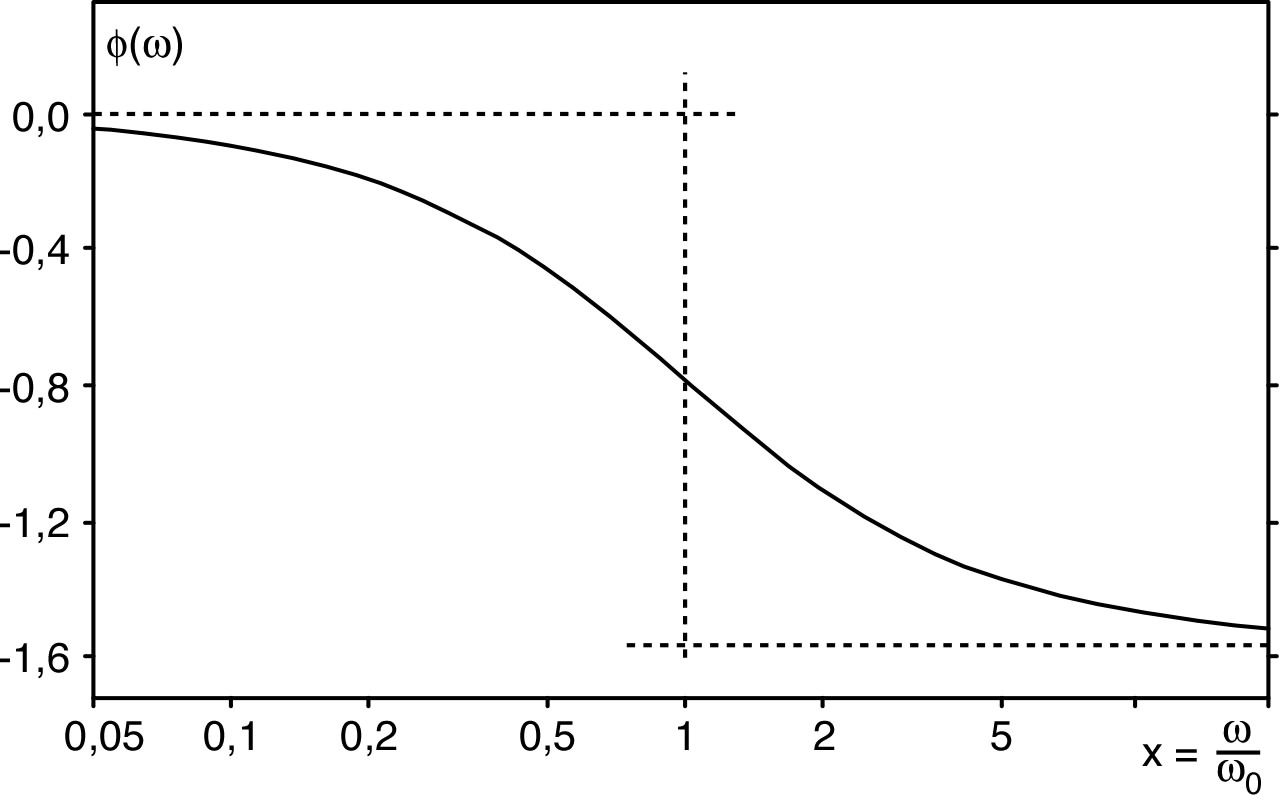
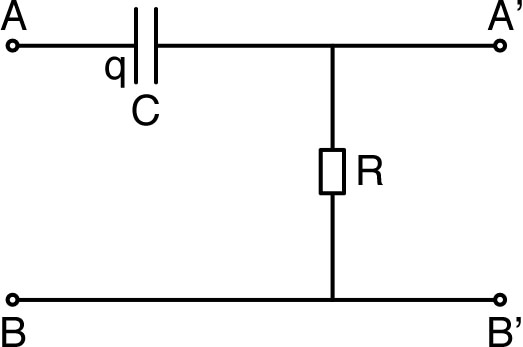
3.3.2. Sens “dérivateur” ; filtre “passe haut”

• De même, un circuit “RC” avec sortie, aux bornes du résistor, sur une charge “infinie” (

\underline{i}_s≈0

donc la sortie n’intervient pas) :

\displaystyle \underline{H}(ω)=\frac{\underline{U}_s}{\underline{U}_e} =\frac{R}{R+\underline{Z}_C}=\frac{\mathrm{j} \,RCω}{1+\mathrm{j} \,RCω}

Ce montage est suiveur à haute fréquence et “dérivateur” à basse fréquence :

\underline{H}(ω)≈\mathrm{j} \,RCω

\displaystyle ω≪ω_0=\frac{1}{RC}

(la dérivation multiplie par

\mathrm{j} \,ω

).

• Le diagramme de Bode pour le gain réel est le suivant :

• On peut délimiter une bande passante, qui dans ce cas particulier ne comporte qu'une “coupure inférieure” pour

ω=ω_0

.

• On obtient aussi pour le déphasage :

\displaystyle ϕ=\frac{π}{2}- \arctan\left(\frac{ω}{ω_0} \right)

📖 exercices n° III, IV, V, VI et VII.