RÉGIME SINUSOÏDAL - QUADRIPÔLES - corrigé des exercices

A. EXERCICES DE BASE

I. Impédance itérative

1.a.	• Pour que le courant débité par le générateur soit le même que s’il était branché sur $R$ , il faut et il suffit que la résistance équivalente de l’ensemble soit $R$ : $\displaystyle r_1+\frac{R \:r_2}{R+r_2}=R$ donc $\displaystyle R=\frac{r_1}{2} \: \left(1+\sqrt{1+\frac{4 \,r_2}{r_1}}\right)$ .

1.b.	• Dans ces conditions : $U_1=R \:I_1$ et $U_0=R \:I_0$ ; par suite : $\displaystyle \frac{P_1}{P_0} =\left(\frac{U_1}{U_0} \right)^2=\left(\frac{R-r_1}{R}\right)^2=\left(\frac{r_2}{R+r_2}\right)^2$ .

2.a.	• Le raisonnement précédent peut s’appliquer par récurrence ; il suffit de considérer un seul élément “LC” du type indiqué. Le calcul est analogue en remplaçant $r_1$ par $\displaystyle \underline{Z}_1=\frac{1}{\mathrm{j} \,Cω}$ et $r_2$ par $\underline{Z}_2=r+\mathrm{j} \,Lω$ ; on obtient ainsi : $\displaystyle \underline{Z}=\frac{1±\sqrt{1-4 \,LCω^2+4 \,\mathrm{j} \,rCω}}{2 \,\mathrm{j} \,Cω}$ . • En constatant alors que le cas indiqué correspond à $4 \,LCω^2=1$ , on obtient après simplification : $\displaystyle \underline{Z}=\frac{1±(1+\mathrm{j}) \: \sqrt{2 \,\mathrm{j} \,rCω}}{2 \,\mathrm{j} \,Cω}$ . On constate alors qu’il y a deux solutions complexes, mais une seule a un argument dans $\left[-\frac{π}{2} \,; \frac{π}{2}\right]$ , c’est-à-dire une partie réelle positive (réalisable à partir de résistances, d’inductances et de capacités) : $\displaystyle \underline{Z}=\frac{1+(1+\mathrm{j}) \: \sqrt{2 \,\mathrm{j} \,rCω}}{2 \,\mathrm{j} \,Cω}=\sqrt{\frac{r}{2 \,Cω}}-\mathrm{j} \,\frac{1+\sqrt{2 \,rCω}}{2 \,Cω}$ .

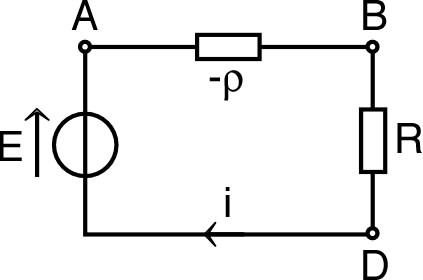
2.b.	• Si on réalise cette impédance par un circuit avec $r_0$ et $C_0$ en série, d’impédance : $\displaystyle \underline{Z}=r_0+\frac{1}{\mathrm{j} \,C_0 \,ω}$ , cela correspond à : $\displaystyle r_0=\sqrt{\frac{r}{2 \,Cω}}=\text{35,4} \:\mathrm{Ω}$ et en reportant : $\displaystyle C_0=\frac{2 \,C \,r_0}{r+r_0}=\text{11,7} \:\mathrm{μF}$ .

II. Adaptation d'impédances

• L'impédance complexe

\underline{Z}

de l'assemblage en parallèle de

R'

C

est telle que :

\displaystyle \frac{1}{\underline{Z}}=\frac{1}{R'}+\mathrm{j} \,Cω

c'est-à-dire :

\displaystyle \underline{Z}=\frac{R'}{1+\mathrm{j} \,R'Cω}

. L'impédance de l'assemblage de

R

L

\underline{Z}

en série est alors :

\underline{Z}'=R+\mathrm{j} \,Lω+\underline{Z}

.
• Le courant débité par le générateur est par suite :

\displaystyle \underline{I}=\frac{\underline{E}}{\underline{Z}'}

et la tension aux bornes de

\underline{Z}

(tension commune à

R'

C

) est :

\displaystyle \underline{U}=\underline{Z} \: \underline{I}=\frac{\underline{E} \: \underline{Z}}{\underline{Z}'}=\frac{\underline{E} \: R'}{R+R'.\,\left(1-LCω^2 \right)+\mathrm{j} \,ω.(L+RR'C)}

.
• Compte tenu de

\underline{U}=R' \:I'

, la puissance (moyenne) dissipée dans

R'

est alors :

\displaystyle P=R' \:{I'}^2=\frac{U^2}{R'}=\frac{{\left|\underline{U}\right|}^2}{R'}=\frac{E^2 \:R'}{\left(R+R'.\,\left(1-LCω^2 \right)\right)^2+ω^2.\left(L+RR'C\right)^2}

• La différentielle de

P

, pour

R

R'

fixées, peut s'écrire sous la forme :

\displaystyle dP=\frac{∂P}{∂L} \: dL+\frac{∂P}{∂C} \: dC

; la valeur maximum est obtenue quand la différentielle est nulle, c'est-à-dire quand

\displaystyle \frac{∂P}{∂L}=0

\displaystyle \frac{∂P}{∂C}=0

. Ces conditions correspondent à :

L-{R'}^2 \,C.\left(1-LCω^2 \right)=0

R^2 \,C-L .\left(1-LCω^2 \right)=0

.
• En régime sinusoïdal (

ω≠0

) et pour

R'≥R

(l'égalité est acceptable) on obtient alors :

\displaystyle C=\frac{1}{R' \,ω} \: \sqrt{\frac{R'-R}{R}}

\displaystyle L=\frac{\sqrt{(R'-R) \: R}}{ω}

◊ remarque : en régime continu (

ω=0

) il semble que la solution soit :

\displaystyle R'=R=\sqrt{\frac{L}{C}}

, mais elle ne décrit pas correctement le problème (en courant continu,

L

C

sont sans effet ; la condition

R'=R

est correcte, mais obtenue ici par hasard puisqu'elle ne peut découler logiquement que de la différentielle

dP

exprimée en fonction de

dR

et/ou

dR'

2.a.

• L'assemblage de

C

en parallèle avec l'ensemble de

R'

L

a une impédance complexe

\underline{Z}

telle que :

\displaystyle \frac{1}{\underline{Z}}=\frac{1}{R'+\mathrm{j} \,Lω}+\mathrm{j} \,Cω

c'est-à-dire :

\displaystyle \underline{Z}=\frac{R'+\mathrm{j} \,Lω}{\left(1-LCω^2 \right)+\mathrm{j} \,R'Cω}

. L'impédance totale de l'assemblage de

R

\underline{Z}

en série est alors :

\underline{Z}'=R+\underline{Z}

.
• Le courant débité par le générateur est par suite :

\displaystyle \underline{I}=\frac{\underline{E}}{\underline{Z}'}

et la tension aux bornes de

\underline{Z}

(tension commune à

C

et à l'ensemble de

R'

L

) est :

\displaystyle \underline{U}=\underline{Z} \: \underline{I}=\frac{\underline{E} \: \underline{Z}}{\underline{Z}'}=\frac{\underline{E}.(R'+\mathrm{j} \,Lω)}{R'+R.\left(1-LCω^2 \right)+\mathrm{j} \,ω.(L+RR'C)}

.
• Le courant circulant dans

R'

(et

L

) est alors :

\displaystyle \underline{I}'=\frac{\underline{U}}{R'+\mathrm{j} \,Lω}

et la tension aux bornes du résistor est donc :

\displaystyle \underline{U}'=R' \:\underline{I}'=\frac{\underline{E} \: R'}{R'+R.\left(1-LCω^2 \right)+\mathrm{j} \,ω.(L+RR'C)}

. La puissance (moyenne) dissipée dans

R'

est par suite :

\displaystyle P=R' \:{I'}^2=\frac{{U'}^2}{R'}=\frac{\left|\underline{U}'\right|^2}{R'}=\frac{E^2 \: R'}{\left(R'+R.\left(1-LCω^2 \right)\right)^2+ω^2.(L+RR'C)^2}

• Le calcul analogue à celui de la question (1) conduit aux conditions :

L-R^2 \,C.\left(1-LCω^2 \right)=0

{R'}^2 \,C-L .\left(1-LCω^2 \right)=0

.
• En régime sinusoïdal (

ω≠0

) et pour

R'≤R

(l'égalité est acceptable) on obtient alors :

\displaystyle C=\frac{1}{R \,ω} \, \sqrt{\frac{R-R'}{R'}}

\displaystyle L=\frac{\sqrt{(R-R') \: R'}}{ω}

◊ remarque : en régime continu, la solution semble ici encore :

\displaystyle R'=R=\sqrt{\frac{L}{C}}

, mais de même elle ne décrit pas correctement le problème (il faut écrire dès le départ les équations avec

ω=0

2.b.

• L'intérêt d'utiliser des éléments “réactifs” est qu’ils peuvent adapter la phase de

\underline{Z}

alors que les résistances ne peuvent adapter que le module

Z

.
• L’avantage de n'utiliser que des éléments “réactifs” est qu'ils ne consomment pas d'énergie par eux mêmes (ils la stockent et la restituent alternativement). Par contre, ils conduisent tout de même à des pertes d'énergie par effet Joule dans

R

III. Fonction de transfert

• Puisque

\underline{i}_s= 0

, c'est le même courant qui circule dans

R

r

C

\displaystyle \underline{i}_e=\frac{\underline{u}_e}{R+r+\frac{1}{\mathrm{j} \,Cω}}

. La tension de sortie, aux bornes de

r

C

, est alors :

\displaystyle \underline{u}_s=\left(r+\frac{1}{\mathrm{j} \,Cω}\right) \: \underline{i}_e

et la fonction de transfert (gain en tension) est donc

\displaystyle \underline{H}=\frac{\underline{u}_s}{\underline{u}_e} =\frac{r+\frac{1}{\mathrm{j} \,Cω}}{R+r+\frac{1}{\mathrm{j} \,Cω}}

• Pour exprimer

\underline{H}

en fonction de

\displaystyle ω_0=\frac{1}{r \,C}

\displaystyle x=\frac{ω}{ω_0}

\displaystyle α=\frac{r}{r+R}

on peut écrire :

\displaystyle \underline{H}=\frac{1+\mathrm{j} \,x}{1+\mathrm{j} \frac{x}{α}}

; ceci peut aussi se mettre sous la forme :

\displaystyle \underline{H}=\frac{α+x^2+\mathrm{j} \:(α-1) \: x}{α.\left(1+\frac{x^2}{α^2} \right)}

• Ainsi :

\displaystyle H(ω)=\left|\underline{H}\right|=\sqrt{\frac{1+x^2}{1+\frac{x^2}{α^2}}}

\displaystyle ϕ=\arg(\underline{H})=\arctan⁡\left(\frac{(α-1) \: x}{α+x^2 }\right)

.
• Le diagramme de Bode pour

H(ω)

est le suivant (en prenant par exemple

α=\text{0,3}

◊ remarque : ce diagramme de Bode présente un point d'inflexion :

H(ω)=\sqrt{α}

pour

x=\sqrt{α}

; par ailleurs, la fréquence de coupure à

-3 \:\mathrm{dB}

correspond à :

\displaystyle x_c=\frac{α}{\sqrt{1-2 \,α^2}}

(inférieure à

ω_0

pour

α=\text{0,3}

) et n'existe que si

α<\frac{1}{\sqrt{2}}

(

H→α

quand

ω→∞

).
• Le diagramme de Bode pour

ϕ(ω)

est le suivant (en prenant par exemple

α=\text{0,3}

• La fonction “

\arctan

” étant strictement monotone, dans l'intervalle de valeurs considéré, l'extremum de

ϕ(ω)

(qui est un minimum) correspond à l'extremum de

\displaystyle \frac{x}{α+x^2}

. On obtient alors

x_m=\sqrt{α}

, d'où on déduit :

\displaystyle ϕ_m=\arctan\left(\frac{α-1}{2 \,\sqrt{α}}\right)

IV. Combinaison de fonctions de transfert

• Puisque

\underline{i}_s=0

, c'est le même courant qui circule dans

R

r

C

\displaystyle \underline{i}_e=\frac{\underline{u}_e}{R+r+\frac{1}{\mathrm{j} \,Cω}}

. La tension de sortie, aux bornes de

r

C

, est alors :

\displaystyle \underline{u}_s=\left(r+\frac{1}{\mathrm{j} \,Cω}\right) \: \underline{i}_e

et la fonction de transfert (gain en tension) est donc

\displaystyle \underline{H}=\frac{\underline{u}_s}{\underline{u}_e} =\frac{r+\frac{1}{\mathrm{j} \,Cω}}{R+r+\frac{1}{\mathrm{j} \,Cω}}

2.	• On peut écrire $\displaystyle \underline{H}=\frac{1+\mathrm{j} \,rCω}{1+\mathrm{j} \,(R+r)\,Cω}=\frac{\underline{H}_1}{\underline{H}_2}$ avec $\displaystyle \underline{H}_1=1+\mathrm{j} \frac{ω}{ω_1}$ et $\displaystyle \underline{H}_2=1+\mathrm{j} \frac{ω}{ω_2}$ .

3.a.	• Pour simplifier on peut ici poser $x=x_k$ et $\underline{H}_k=1+\mathrm{j} \,x$ ; les deux cas sont alors analogues. • Ainsi : $H_k (ω)=\left\|\underline{H}_k (ω)\right\|=\sqrt{1+x^2}$ . Pour $x≈0$ le montage est suiveur : $H_k≈1$ et $H_{k\mathrm{dB}}≈0$ ; pour $x≈∞$ le montage est dérivateur : $H_k≈x$ et $H_{k\mathrm{dB}}≈20 \; \log⁡(x)$ . Les deux asymptotes se coupent pour $x=1$ .

3.b.	• On obtient ici : $ϕ_k (ω)=\arg(\underline{H}_k (ω))=\arctan⁡(x)$ . Pour $x≈0$ le montage est suiveur : $ϕ_k≈0$ ; pour $x≈∞$ le montage est dérivateur : $ϕ_k≈\frac{π}{2}$ . • Pour $x≈1$ on est ramené à étudier le développement limité par rapport à $ξ=\log⁡(x)≈0$ ; ainsi : $\displaystyle ϕ_k≈\arctan⁡(1)+\frac{d}{dξ} \left(\arctan\left(10^ξ \right) \right) \: ξ≈\frac{π}{4}+\frac{\ln(10)}{2} \: ξ$ . Ceci correspond à une droite coupant les asymptotes pour $\displaystyle \frac{\ln⁡(10)}{2} \: ξ=±\frac{π}{4}$ donc pour $ξ=\log⁡(x)=±\frac{π}{2} \: \log⁡(\mathrm{e})$ ; $x=\mathrm{e}^{±π/2}$ .

4.a.	• On peut écrire : $\displaystyle H(ω)=\left\|\frac{\underline{H}_1}{\underline{H}_2} \right\|$ donc : $H_{\mathrm{dB}}=20 \; \log(H_1)-20 \; \log(H_2)=H_{1\mathrm{dB}}-H_{2\mathrm{dB}}$ . • Pour $ω<ω_2$ on obtient $H_{1\mathrm{dB}}≈H_{2\mathrm{dB}}≈0$ donc $H_{\mathrm{dB}}≈0$ (dans l'approximation asymptotique). • Pour $ω_2<ω<ω_1$ on obtient $H_{1\mathrm{dB}}≈0$ et $H_{2\mathrm{dB}}≈20 \; \log(x_2)$ avec $\displaystyle x_2=\frac{x_1}{α}$ ; ceci donne donc : $H_{\mathrm{dB}}≈20 \; \log(α)-20 \; \log(x_1)$ . • Pour $ω_1<ω$ on obtient $H_{1\mathrm{dB}}≈20 \; \log(x_1)$ et $H_{2\mathrm{dB}}≈20 \; \log(x_2)$ donc : $H_{\mathrm{dB}}≈20 \; \log(α)$ . • Le diagramme de Bode simplifié pour $H(ω)$ est donc le suivant. ◊ remarque : ce diagramme de Bode présente un point d'inflexion : $H(ω)=\sqrt{α}$ pour $x_1=\sqrt{α}$ ; par contre, l'approximation au niveau de ce point d'inflexion est assez médiocre si $α$ est trop proche de $1$ , car la zone correspondante n'est pas dans les portions bien représentées par les asymptotes.

4.b.	• De façon analogue $ϕ=\arg(\underline{H})=\arg(\underline{H}_1)-\arg(\underline{H}_2)=ϕ_1-ϕ_2$ . • Pour $\log(x_2)<-\frac{π}{2} \, \log⁡(\mathrm{e})$ c'est-à-dire $\log(x_1)<\log(α)-\frac{π}{2} \, \log(\mathrm{e})$ on obtient : $ϕ_1≈ϕ_2≈0$ donc $ϕ≈0$ (dans l'approximation asymptotique). • Pour $-\frac{π}{2} \: \log(\mathrm{e})<\log(x_1)<\log(α)+\frac{π}{2} \: \log(\mathrm{e})$ les variations affines analogues de $ϕ_1$ et $ϕ_2$ donnent une différence constante : $\displaystyle ϕ≈\frac{\ln⁡(10)}{2} \: \log(α)≈-\text{0,60} \:\mathrm{rad}$ . • Pour $\frac{π}{2} \: \log(\mathrm{e})<\log(x_1)$ on obtient $ϕ_1≈ϕ_2≈\frac{π}{2}$ donc : $ϕ≈0$ . • Dans les deux zones intermédiaires, le raccordement se fait de façon affine. • Le diagramme de Bode simplifié pour $ϕ(ω)$ est donc le suivant.

4.c.	• La courbe réelle présente des “arrondis” au niveau des raccordements du diagramme simplifié. L'extremum de $ϕ(ω)$ (qui est un minimum) correspond par symétrie au milieu de l'intervalle “minimum” représenté ici : $\displaystyle \log(x_m)=\frac{\log(α)+\log(1)}{2}$ donc $x_m=\sqrt{α}$ . • D'après ce qui précède, le minimum est : $\displaystyle ϕ_m≈\frac{\ln⁡(10)}{2} \: \log(α)=\ln(\sqrt{α})$ ; compte tenu des approximations, ce n'est a priori qu'un ordre de grandeur.

V. Circuit “RLC” et fonction de transfert

• Puisque

\underline{i}_s=0

, c'est le même courant qui circule dans

R

L

C

\displaystyle \underline{i}_e=\frac{\underline{u}_e}{R+\mathrm{j}.\left(Lω-\frac{1}{Cω}\right)}

. La tension de sortie, aux bornes de

R

, est alors :

\underline{u}_s=R \:\underline{i}_e

et la fonction de transfert (gain en tension) est par conséquent :

\displaystyle \underline{H}=\frac{\underline{u}_s}{\underline{u}_e} =\frac{R}{R+\mathrm{j}.\left(Lω-\frac{1}{Cω}\right)}

• En fonction de

\displaystyle ω_0=\frac{1}{\sqrt{L \,C}}

\displaystyle x=\frac{ω}{ω_0}

\displaystyle 𝒬=\frac{Lω_0}{R}=\frac{1}{RCω_0}

on obtient :

\displaystyle \underline{H}=\frac{1}{1+\mathrm{j} \,𝒬.(x-\frac{1}{x})}

.
• On en déduit :

\displaystyle H(ω)=\left|\underline{H}\right|=\frac{1}{\sqrt{1+𝒬^2.\left(x-\frac{1}{x}\right)^2}}

ϕ=\arg(\underline{H})=-\arctan\left(𝒬.\left(x-\frac{1}{x}\right)\right)

.
• Le diagramme de Bode pour

H(ω)

est le suivant pour

𝒬=10

(résonance aiguë).

• Le diagramme est le suivant pour

𝒬=\text{0,5}

(résonance large).

• Le diagramme de Bode pour

ϕ(ω)

est le suivant (en prenant pour exemples

𝒬=10

𝒬=\text{0,5}

• On peut écrire :

\displaystyle G_{\mathrm{dB}}=20 \; \log\left(\frac{H(ω)}{H(ω_0)}\right)

; ainsi en particulier :

\displaystyle G_{\mathrm{dB}}≈20 \; \log\left(\frac{x}{𝒬}\right)

pour

ω≪ω_0

et de même :

\displaystyle G_{\mathrm{dB}}≈20 \; \log\left(\frac{1}{𝒬 \,x}\right)

pour

ω≫ω_0

.
• La bande passante à

-3 \:\mathrm{dB}

en puissance est limitée par

ω

tel que

\displaystyle H(ω)=\frac{H(ω_0)}{\sqrt{2}}=\frac{1}{\sqrt{2}}

, c'est-à-dire

\displaystyle ω^2±\frac{ω_0}{𝒬}-ω_0^{\:2}=0

. Les solutions positives

\displaystyle ω_1=\frac{ω_0}{2 \,𝒬} \:\left(\sqrt{1+4 \,𝒬^2}-1\right)

\displaystyle ω_2=\frac{ω_0}{2 \,𝒬} \:\left(\sqrt{1+4 \,𝒬^2}+1\right)

donnent la bande passante :

\displaystyle ∆ω=ω_2-ω_1=\frac{ω_0}{𝒬}

VI. Fonctions de transfert

• L’impédance complexe équivalente à l'ensemble de

C

R_c

peut s’écrire :

\displaystyle \underline{Z}_1=\frac{1}{\mathrm{j} \,Cω+\frac{1}{R_c}}=\frac{R_c}{1+\mathrm{j} \,R_c \, Cω}

.
• D'après le principe du pont diviseur de tension :

\displaystyle \underline{H}_u=\frac{\underline{u}_s}{\underline{u}_e} =\frac{\underline{Z}_1}{R+\underline{Z}_1}=\frac{R_c}{R.(1+\mathrm{j} \,R_c \, Cω)+R_c}

2.	• D'après le principe du pont diviseur de courant : $\displaystyle \underline{H}_i=\frac{\underline{i}_s}{\underline{i}_e} =\frac{G_c}{\underline{Y}_1} =\frac{\underline{Z}_1}{R_c} =\frac{1}{1+\mathrm{j} \,R_c \, Cω}$ .

• Le gain en puissance moyenne peut s'écrire :

\displaystyle H_P=\frac{P_s}{P_e} =\frac{U_s \: I_s \: \cos(ϕ_s )}{U_e \: I_e \: \cos(ϕ_e )}=H_u \: H_i \, \frac{\cos(ϕ_s )}{\cos(ϕ_e )}

.
• Par ailleurs :

\displaystyle H_u=\left|\underline{H}_u \right|=\frac{R_c}{\sqrt{(R+R_c )^2+(RR_c \,Cω)^2}}

;

\displaystyle H_i=\left|\underline{H}_i \right|=\frac{1}{\sqrt{1+(R_c \, Cω)^2}}

;

\underline{u}_s=R_c \: \underline{i}_s

;

\cos(ϕ_s )=\cos(\arg(R_c ))=1

;

\underline{u}_e=(R+\underline{Z}_1 ) \;\underline{i}_e

;

\displaystyle ϕ_e=\arg(R+\underline{Z}_1)=\arg\left(\frac{R.(1+\mathrm{j} \,R_c \: Cω)+R_c.(1-\mathrm{j} \,R_c \: Cω)}{1+(R_c \:Cω)^2}\right)

;

\displaystyle \cos(ϕ_e )=\cos\left(\arg\left(R+R_c+\mathrm{j} \,R_c \, Cω .(R-R_c )\right)\right)=\frac{R+R_c}{\sqrt{(R+R_c )^2+(R_c \, Cω)^2 \:(R-R_c )^2}}

• Finalement :

\displaystyle H_P=\frac{R_c}{R+R_c} \: \frac{\sqrt{(R+R_c )^2+(R_c \: Cω)^2 \:(R-R_c )^2}}{\sqrt{(R+R_c )^2+(RR_c \: Cω)^2 \: \sqrt{1+(R_c \: Cω)^2}}}

VII. Filtre et fonction de transfert

1.	• L’impédance complexe équivalente peut s’écrire : $\displaystyle \underline{Z}_e=\mathrm{j}\, Lω+\frac{1}{\mathrm{j} \,Cω+\frac{1}{\underline{Z}_c+\mathrm{j} \,Lω}}=\mathrm{j} \,Lω+\frac{\underline{Z}_c+\mathrm{j} \,Lω}{1+\mathrm{j} \,Cω.(\underline{Z}_c+\mathrm{j} \,Lω)}$ .

• La condition :

\displaystyle \underline{Z}_{it}=\mathrm{j} \,Lω+\frac{1}{\mathrm{j} \,Cω+\frac{1}{\underline{Z}_{it}+\mathrm{j} \,Lω}}

correspond à :

\displaystyle \underline{Z}_{it}^{\:2}=\frac{2 \,L}{C}-L^2 \,ω^2

(valeur réelle).
• On constate que

\underline{Z}_{it}^{\:2}=0

pour

\displaystyle ω=ω_1=\sqrt{\frac{2}{L \,C}}

. De plus, on obtient ainsi :

\underline{Z}_{it}^{\:2}>0

pour

ω<ω_1

, ce qui correspond à une impédance

\underline{Z}_{it}

réelle (purement résistive) ; on obtient de même :

\underline{Z}_{it}^{\:2}<0

pour

ω>ω_1

, ce qui correspond à une impédance

\underline{Z}_{it}

imaginaire (purement réactive).
◊ remarque : on peut écrire ainsi :

\underline{Z}_{it}=L \:\sqrt{ω_1^{\:2}-ω^2}

• La loi des mailles donne :

\displaystyle (\underline{Z}_c+\mathrm{j} \,Lω) \; \underline{i}_s=\frac{\underline{i}_e-\underline{i}_s}{\mathrm{j} \,Cω}

d’où on déduit :

\underline{i}_e=\underline{i}_s .\left[1+\mathrm{j} \,Cω .(\underline{Z}_c+\mathrm{j} \,Lω)\right]

. La fonction de transfert est :

\displaystyle \underline{H}=\frac{\underline{u}_s}{\underline{u}_e} =\frac{\underline{Z}_c \: \underline{i}_s}{\underline{Z}_e \: \underline{i}_e}=\frac{\underline{Z}_c}{\underline{Z}_c .\left(1-LCω^2 \right)+\mathrm{j} \,Lω.\left(2-LCω^2 \right)}

• Si on ajuste

\underline{Z}_c=\underline{Z}_{it} (ω)=L \:\sqrt{ω_1^{\:2}-ω^2}=\underline{Z}_e

on obtient :

\displaystyle \underline{H} (ω)=\frac{1}{1-LCω^2+\mathrm{j} \,LCω.\sqrt{ω_1^{\:2}-ω^2}}

.
• En particulier pour

ω<ω_1

on obtient :

\displaystyle H(ω)=\frac{1}{\sqrt{\left(1-LCω^2 \right)^2+L^2 \,C^2 \,ω^2.(ω_1^{\:2}-ω^2 )}}=1

;

\displaystyle ϕ(ω)=-\arctan\left(\frac{ω\: \sqrt{ω_1^{\:2}-ω^2}}{ω_0^{\:2}-ω^2}\right)

avec

\displaystyle ω_0=\frac{1}{\sqrt{L \,C}}

• De même, pour

ω>ω_1

\displaystyle H(ω)=\frac{1}{LCω^2-1+LCω.\sqrt{ω^2-ω_1^{\:2}}}

ϕ(ω)=π

(

\underline{H} (ω)

réel mais négatif).
• Ceci peut être résumé par les représentations graphiques suivantes.

B. EXERCICE D'APPROFONDISSEMENT

VIII. Diode tunnel ; auto-oscillation et amplification

• D’après le schéma, la tension aux bornes de la diode peut s’écrire :

U_{AB}=E-R \:I

; le “point de fonctionnement” sur le graphique correspond donc à l’intersection de la courbe caractéristique avec la droite d’équation :

\displaystyle I=\frac{E-U}{R}

. La valeur indiquée pour

R

donne une conductance

\displaystyle G=\frac{1}{R}≈\text{6,9} \:\mathrm{mS}

et la valeur de

E

est telle que la droite précédente est proche de celle représentée sur le graphique.
• Inversement, la pente indiquée sur le graphique correspond à une résistance

-ρ

avec

ρ=150 \:\mathrm{Ω}

. Puisque le point de fonctionnement est au voisinage du point indiqué (

U_1=200 \:\mathrm{mV}

I_1=\text{0,5} \:\mathrm{mA}

) on peut alors obtenir le résultat par un calcul algébrique, en assimilant la portion “centrale” de la caractéristique avec la droite d’équation :

U_{AB}=U_1-ρ.(I-I_1 )

. On obtient ainsi le point d’intersection pour

U_0=U_1=200 \:\mathrm{mV}

I_0=I_1=\text{0,5} \:\mathrm{mA}

• Soumis à une f.e.m.

E=E_0+e≈E_0

le circuit est parcouru par un courant

I=I_0+i≈I_0

et la tension aux bornes de la diode est donc :

U=E-R \:I=U_0+(e-R \:i)≈U_0

. Or, au voisinage de ce point de fonctionnement, la caractéristique peut être décrite par :

U=U_0-ρ.(I-I_0 )

; la tension variable ajoutée de ce fait à

U_0

est donc :

U-U_0=-ρ \:i

, ce qui est caractéristique d’une résistance négative

-ρ

.
◊ remarque : le signe négatif ne provient pas d’un choix arbitraire du sens de mesure de la tension (elle est mesurée dans le même sens que celui qui donnerait une résistance positive pour un résistor) ; ce signe négatif est associé à la pente négative de la caractéristique (sur la portion considérée).

• Le montage peut ainsi être représenté (pour le régime variable) par le schéma ci-contre.

• On obtient dans ces conditions :

u=R \:i

e=(R-ρ) \:i

donc :

\displaystyle 𝒜=\frac{u}{e}=\frac{R}{R-ρ}

• Si la résistance

R

est donnée, la seule façon de modifier

𝒜

est de changer

ρ

. Si la diode tunnel est donnée, on peut modifier

ρ

en utilisant un autre point de fonctionnement sur la caractéristique, c’est-à-dire en imposant

E_0

différent (et donc

U_0

I_0

différents) pour se placer en un point de la caractéristique dont la pente est différente.

• On obtient dans ces conditions :

\underline{u}=R \:\underline{i}

\displaystyle \underline{e}=\left(R+\mathrm{j} \,Lω-\frac{ρ}{1-\mathrm{j} \,ρCω}\right) \;\underline{i}

; par conséquent :

\displaystyle \underline{𝒜}=\frac{\underline{u}}{\underline{e}}=\frac{R}{R+\mathrm{j} \,Lω-\frac{ρ}{1-\mathrm{j} \,ρCω}}=\frac{R.(1-\mathrm{j} \,ρCω)}{R-ρ.\left(1-LCω^2 \right)+\mathrm{j} \,ω.(L-ρRC)}

• L’argument de

\underline{𝒜}

correspond au déphasage de

u

par rapport à

e

\displaystyle \underline{𝒜}=𝒜 \:\mathrm{e}^{\mathrm{j}ϕ}=\frac{U_m \: \mathrm{e}^{\mathrm{j}ϕ'}}{E_m \: \mathrm{e}^{\mathrm{j}ϕ''}}

(où

U_m

E_m

désignent les amplitudes des variations

u

e

) correspond à

ϕ=ϕ'-ϕ''

• Le module

𝒜(ω)

est infini si et seulement si le dénominateur est nul, donc :

R-ρ.\left(1-LCω^2 \right)=0

L-ρRC=0

. Ceci donne :

\displaystyle R_c=\frac{L}{ρ \,C}

ω_c=\sqrt{ω_0^{\:2}-α^2}

avec

\displaystyle ω_0=\frac{1}{\sqrt{L \,C}}

(pulsation propre du circuit “LC”) et

\displaystyle α=-\frac{1}{ρ \,C}

(inverse de la constante de temps caractéristique de “l’amortissement” par le circuit “ρC” ; d’ailleurs dans ces conditions identique, au signe près, à la constante de temps du circuit “R_cL”).
◊ remarque : ceci suppose

\left|α\right|<ω_0

(amortissement relativement faible).
• En fait, dans ces conditions, le circuit “ρC” ne réalise par un “amortissement” mais une amplification ; le gain obtenu est infini car l’amortissement causé par “R_cL” est exactement compensé par l’amplification causée par “ρC”. Par suite, le circuit total reçoit de l’énergie (fournie par le générateur) qui n’est pas dissipée, donc l’accumulation de cette énergie fait tendre l’amplitude du signal vers l’infini.
• Dans la mesure où les calculs précédents ne considèrent que le régime sinusoïdal asymptotique (après “amortissement” du régime transitoire), ce régime asymptotique correspond forcément à une amplitude infinie.
◊ remarque : si on changeait

R

pour lui donner la valeur

R_c

il faudrait aussi changer

E_0

si on voulait conserver le même point de fonctionnement (d’où découle

ρ

6.a.	• On peut écrire : $\displaystyle 𝒜^2=\frac{R^2.\left(1+(ρCω)^2 \right)}{\left(R-ρ.\left(1-LCω^2 \right)\right)^2+ω^2.(L-ρRC)^2}$ . • Pour $ω→0$ on obtient $\displaystyle ω≪\left\|α\right\|=\frac{1}{ρ \,C}=\text{1,33}.{10}^9 \: \mathrm{s^{-1}}$ donc $\displaystyle ω≪ω_0=\frac{1}{\sqrt{L \,C}}=\text{1,83}.{10}^{10} \: \mathrm{s^{-1}}$ ; on peut donc écrire : $\displaystyle 𝒜^2≈\frac{R^2}{(R-ρ)^2+ω^2.(L-ρRC)^2}$ . • En particulier, tant que $ω$ n’est pas trop grand, on obtient : $\displaystyle 𝒜≈𝒜(0)=\frac{R}{\left\|R-ρ\right\|} =29>1$ ; cette valeur est d’ailleurs la valeur maximum $𝒜_{max}$ . ◊ remarque : il est normal de retrouver ici l’expression obtenue en négligeant $L$ et $C$ , puisqu’à faible fréquence l’impédance de $L$ est négligeable et que celle de $C$ est quasi-infinie (imposant ainsi le passage du courant dans $-ρ$ ).

6.b.	• Compte tenu du domaine de validité de l’approximation précédente (indiquée en pointillés sur le graphique ci-après), la bande passante peut être calculée avec l’expression simplifiée. • La limite (supérieure) de la bande passante correspond à : $(R-ρ)^2+ω_1^{\:2}.(L-ρRC)^2=2 \,(R-ρ)^2$ c’est-à-dire : $\displaystyle ∆ω=ω_1=\frac{\left\|R-ρ\right\|}{\left\|L-ρRC\right\|} =\text{46,2}.{10}^6 \: \mathrm{rad.s^{-1}}$ .