RÉGIME SINUSOÏDAL ; FONCTIONS DE TRANSFERT

RÉGIME SINUSOÏDAL ; FONCTIONS DE TRANSFERT - corrigé du TP

3. Mesures et courbes

3.1. Sortie aux bornes de la résistance $R_0$

• De nombreuses combinaisons de valeurs pour

R

L

C

sont possibles. On peut par exemple considérer le montage avec :

R_0=\text{46,18}±\text{0,25} \:\mathrm{Ω}

;

L=\text{67,9}±\text{0,9} \:\mathrm{mH}

;

r=\text{12,0}±\text{0,3} \:\mathrm{Ω}

;

C=\text{0,50}±\text{0,03} \:\mathrm{μF}

.

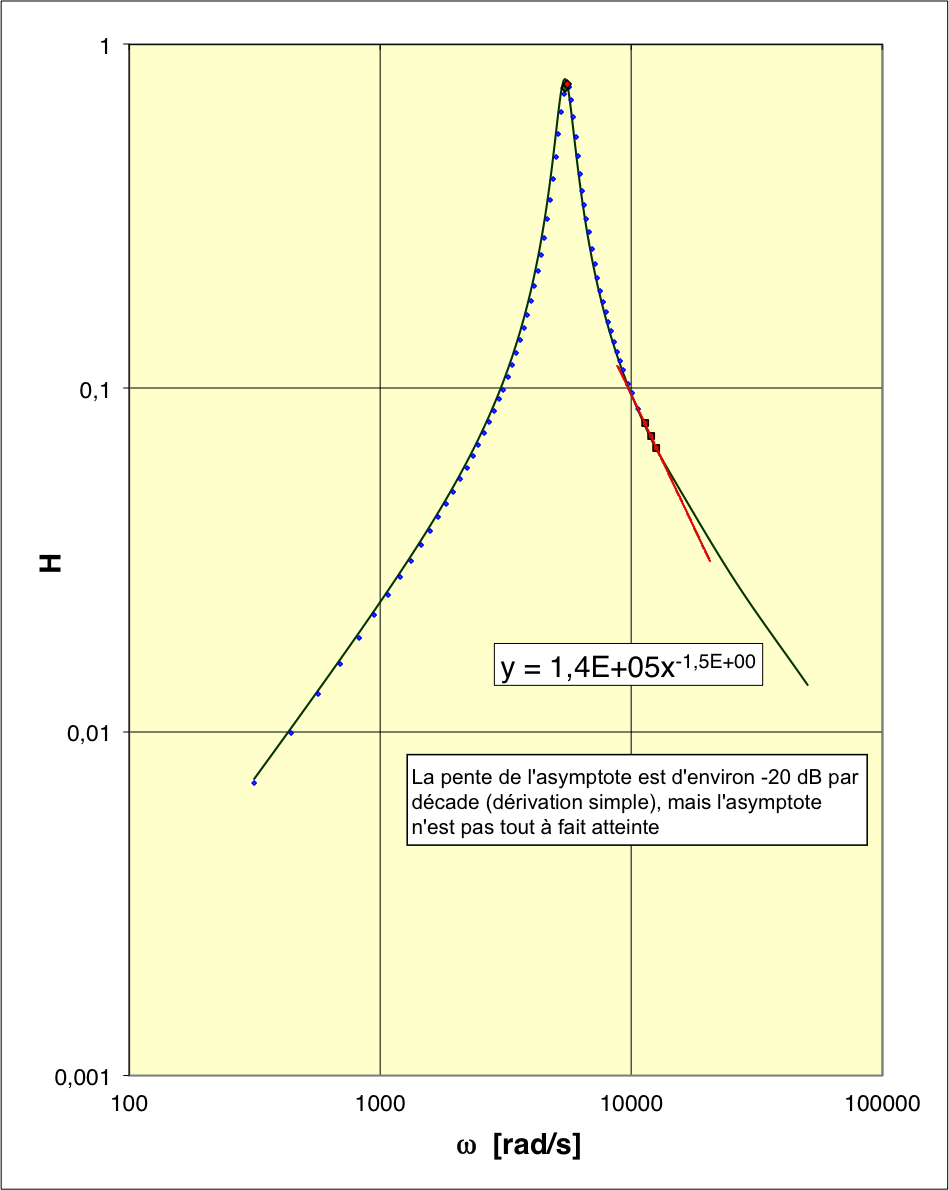
• On obtient ainsi pour

H(ω)

une résonance très marquée.

En pratique, si l'énoncé conseille de mesurer dans l'intervalle de

≈50 \:\mathrm{Hz}

jusqu'à au moins

≈2000 \:\mathrm{Hz}

, il est clair que cela dépend du choix des paramètres : ici la fréquence de résonance un peu élevée aurait dû inciter à poursuivre les mesures jusqu'à

≈5000 \:\mathrm{Hz}

(voire plus) afin de mieux observer l'asymptote des hautes fréquences (c'est l'intérêt de tracer le graphique en même temps que les mesures).

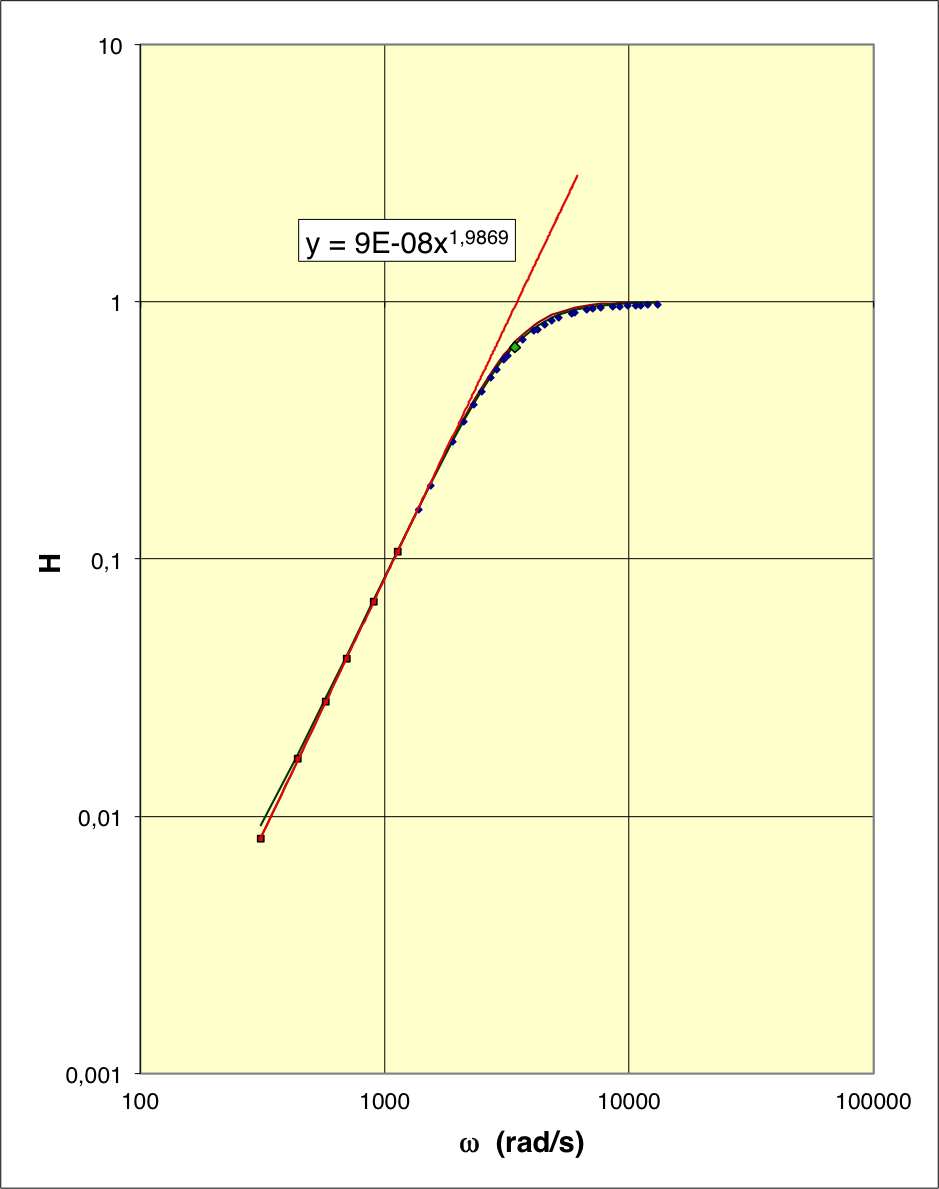
• Le modèle théorique (déduit du cours pour les valeurs choisies des composants RLC) représente plutôt correctement les données, mais le maximum est légèrement surestimé et correspond à une fréquence de résonance un peu sous-estimée ; les écarts sont toutefois comparables aux incertitudes de mesure.

Le gain peut s'écrire

\displaystyle H=\frac{R_0}{\sqrt{R^2+\left(Lω-\frac{1}{Cω}\right)^2}}

et le maximum théorique correspond à l'annulation de la réactance ; ainsi :

\displaystyle H_{max}=\frac{R_0}{R}=\text{0,794}±\text{0,005}

et la pulsation de résonance :

\displaystyle ω_r=ω_0=\frac{1}{\sqrt{L \,C}}=5427±170 \:\mathrm{rad.s^{-1}}

.

Les pulsations de coupure correspondent à :

ω_1=5135±60 \:\mathrm{rad.s^{-1}}

ω_2=5955±65 \:\mathrm{rad.s^{-1}}

; la bande passante est donc :

∆ω=820±125 \:\mathrm{rad.s^{-1}}

à comparer à

\displaystyle \frac{R}{L}=857±19 \:\mathrm{rad.s^{-1}}

.

Le facteur de qualité est

\displaystyle 𝒬=\frac{ω_0}{∆ω}=\text{6,6}±\text{1,2}

(

𝒬≫1

correspond à une résonance très marquée).

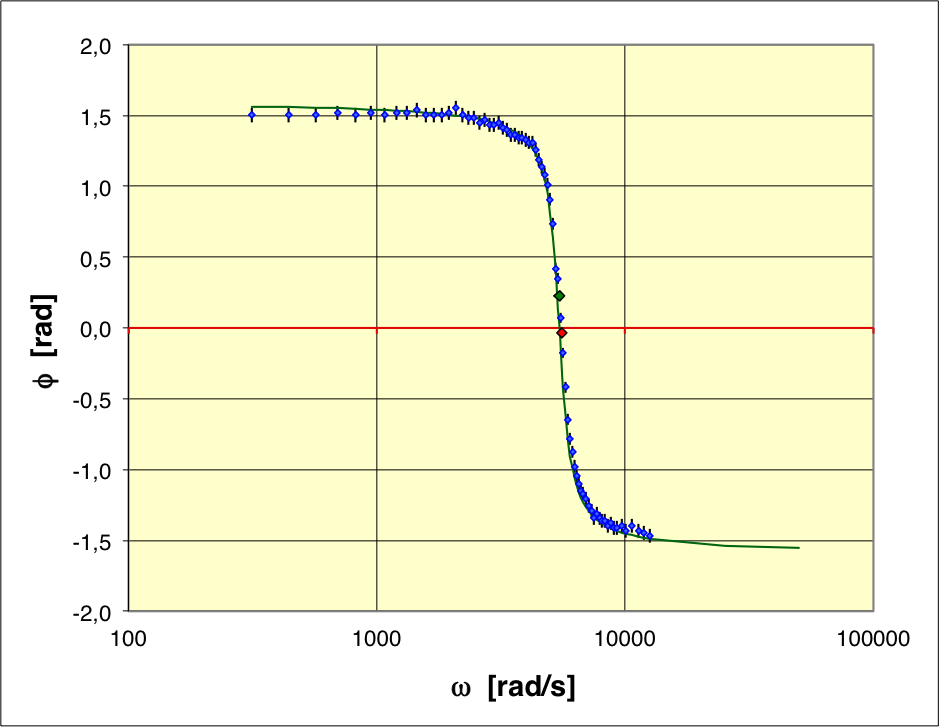
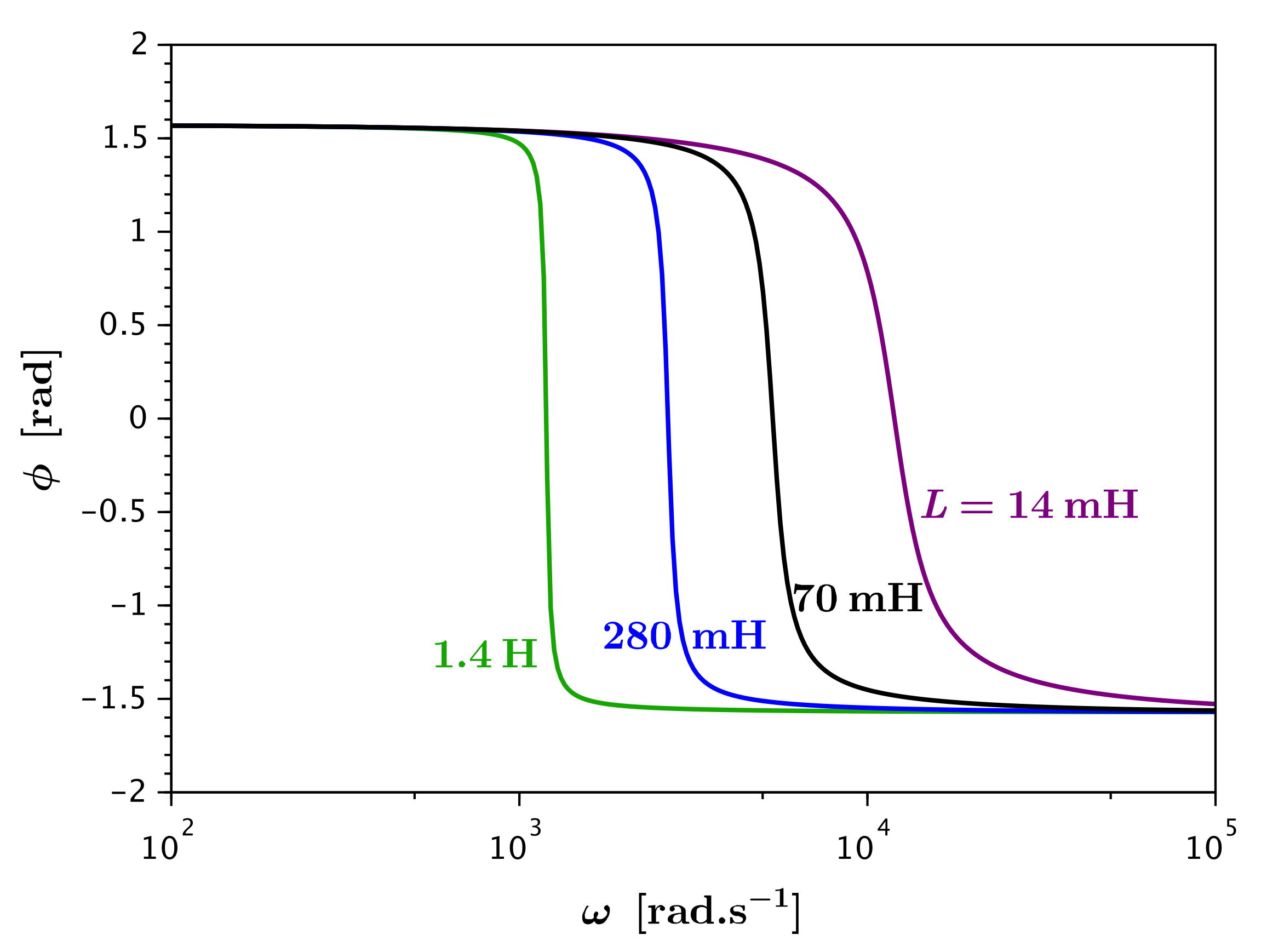
• On obtient ainsi pour

ϕ(ω)

une résonance très marquée (bascule de phase brutale).

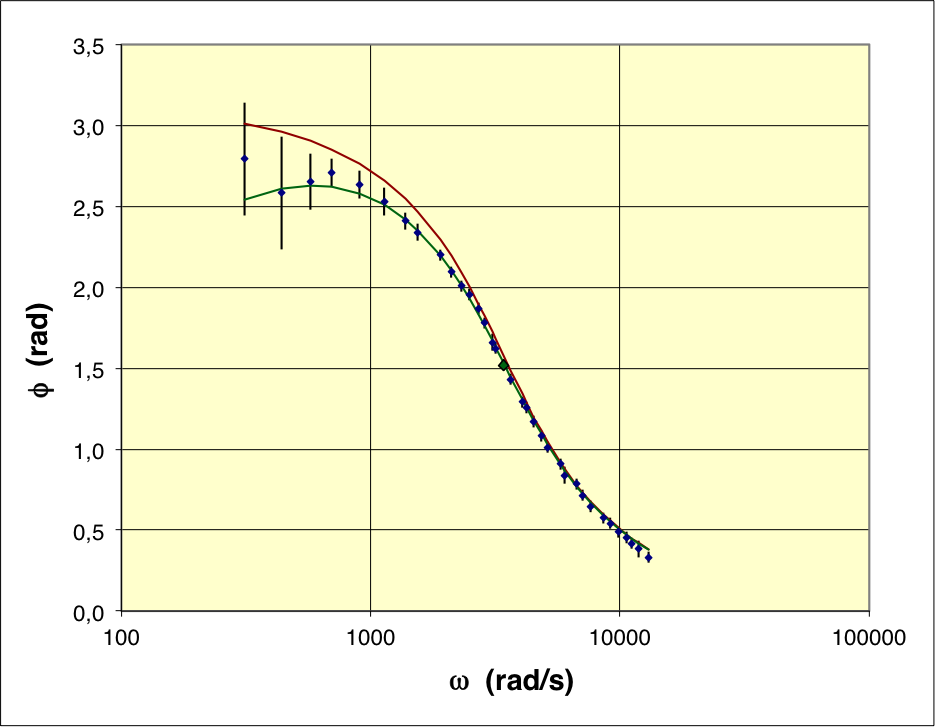
• Le déphasage peut s'écrire

\displaystyle ϕ=\arctan\left(\frac{Lω-\frac{1}{Cω}}{R}\right)

; ce modèle théorique représente plutôt correctement les données. Le passage par

ϕ=0

est en accord avec le maximum de

H

et correspond à une fréquence de résonance un peu sous-estimée par le modèle ; les écarts sont toutefois comparables aux incertitudes de mesure. Les passages par

ϕ=±\frac{π}{4}

sont en accord avec les pulsations de coupures déterminées d'après

H

(les écarts sont comparables aux incertitudes de mesure).

3.2. Sortie aux bornes du condensateur

• On considère ici :

R_0=\text{47,5}±\text{2,6} \:\mathrm{Ω}

;

L=\text{66,0}±\text{0,9} \:\mathrm{mH}

;

r=\text{11,0}±\text{0,8} \:\mathrm{Ω}

;

C=\text{11,53}±{0,14} \:\mathrm{μF}

.

• Un intérêt à ce choix est qu'on obtient ainsi pour

H(ω)

une résonance moins marquée.

Ici la fréquence de résonance moins élevée aurait normalement permis de bien observer l'asymptote des hautes fréquences ; hélas les mesures n'ont pas dépassé

≈800 \:\mathrm{Hz}

(alors que l'énoncé conseille jusqu'à au moins

≈2000 \:\mathrm{Hz}

). Par chance, cela suffit tout de même pour une observation raisonnable.

Une différence de comportement, par rapport au cas précédent, est que la limite à basse fréquence (régime capacitif) est

H→1

• Le modèle théorique (déduit du cours pour les valeurs choisies des composants RLC) représente plutôt correctement les données, mais le maximum est légèrement surestimé ; les écarts sont toutefois comparables aux incertitudes de mesure.

Le gain peut s'écrire

\displaystyle H=\frac{\frac{1}{Cω}}{\sqrt{R^2+\left(Lω-\frac{1}{Cω}\right)^2}}

; le maximum correspond au minimum de

R^2 C^2 ω^2+(LCω^2-1)^2

. En notant

\displaystyle w=\frac{ω^2}{ω_0^{\:2}}

κ=R^2 C^2 ω_0^{\:2}

la dérivée de

κ \:w +(w-1)^2

s'annule pour

\displaystyle w=1-\frac{κ}{2}

; ceci correspond à :

ω_r=ω_0 \: \sqrt{1-\frac{1}{2} R^2 C^2 ω_0^{\:2}}<ω_0

.

On obtient ici :

\displaystyle ω_0=\frac{1}{\sqrt{L \,C}}=1146±14 \:\mathrm{rad.s^{-1}}

;

ω_r=960±36 \:\mathrm{rad.s^{-1}}

;

H_{max}=\text{1,40}±\text{0,07}

.

Les pulsations de coupure correspondent à :

ω_1≈0

ω_2=1320±40 \:\mathrm{rad.s^{-1}}

; compte tenu du fait que

H_{max}≈\sqrt{2}

ce cas correspond à la limite au delà de laquelle il n'y aurait pas de coupure inférieure. La bande passante est donc :

∆ω=1320±40 \:\mathrm{rad.s^{-1}}

; on peut comparer à

\displaystyle \frac{R}{L}=886±63 \:\mathrm{rad.s^{-1}}

(valable pour la sortie aux bornes de la résistance) mais seul l'ordre de grandeur correspond vaguement car la résonance n'est pas très marquée.

Le facteur de qualité est

\displaystyle 𝒬=\frac{ω_0}{∆ω}=\text{0,87}±\text{0,04}

(

𝒬≈1

correspond à une résonance peu marquée).

• On obtient également pour

ϕ(ω)

une résonance moins marquée (bascule de phase plus progressive).

• Le modèle théorique (juste décalé de

\frac{π}{2}

par rapport au cas précédent) représente plutôt correctement les données (sauf les derniers points). Le passage par

ϕ=-\frac{π}{2}

est en accord avec

ω_0

.

Les pulsations de coupures sont ici définies autrement pour le déphasage ; la coupure supérieure pour le passage par

ϕ=-\frac{3 \,π}{4}

est

ω_2=1640±40 \:\mathrm{rad.s^{-1}}

; la coupure inférieure pour le passage par

ϕ=-\frac{π}{4}

est

ω_1=780±40 \:\mathrm{rad.s^{-1}}

; la bande passante est donc :

∆ω=860±80 \:\mathrm{rad.s^{-1}}

compatible avec

\displaystyle \frac{R}{L}

(cette définition par le déphasage est sur ce point plus pratique).

Cela correspond à un facteur de qualité

\displaystyle 𝒬=\frac{ω_0}{∆ω}=\text{1,33}±\text{0,14}

(

𝒬≈1

correspond ici aussi à une résonance peu marquée).

3.3. Sortie aux bornes de la bobine

• On considère ici :

R_0={399,8}±{2,2} \:\mathrm{Ω}

;

L={82,0}±{1,0} \:\mathrm{mH}

;

r=\text{12,8}±\text{0,3} \:\mathrm{Ω}

;

C=\text{1,035}±{0,010} \:\mathrm{μF}

.

• Un intérêt à ce choix (sur-critique) est qu'ainsi pour

H(ω)

on n'obtient pas vraiment de résonance (seulement une élimination des basses fréquences).

Une différence de comportement, par rapport aux cas précédents, est que la limite à haute fréquence (régime inductif) est

H→1

.

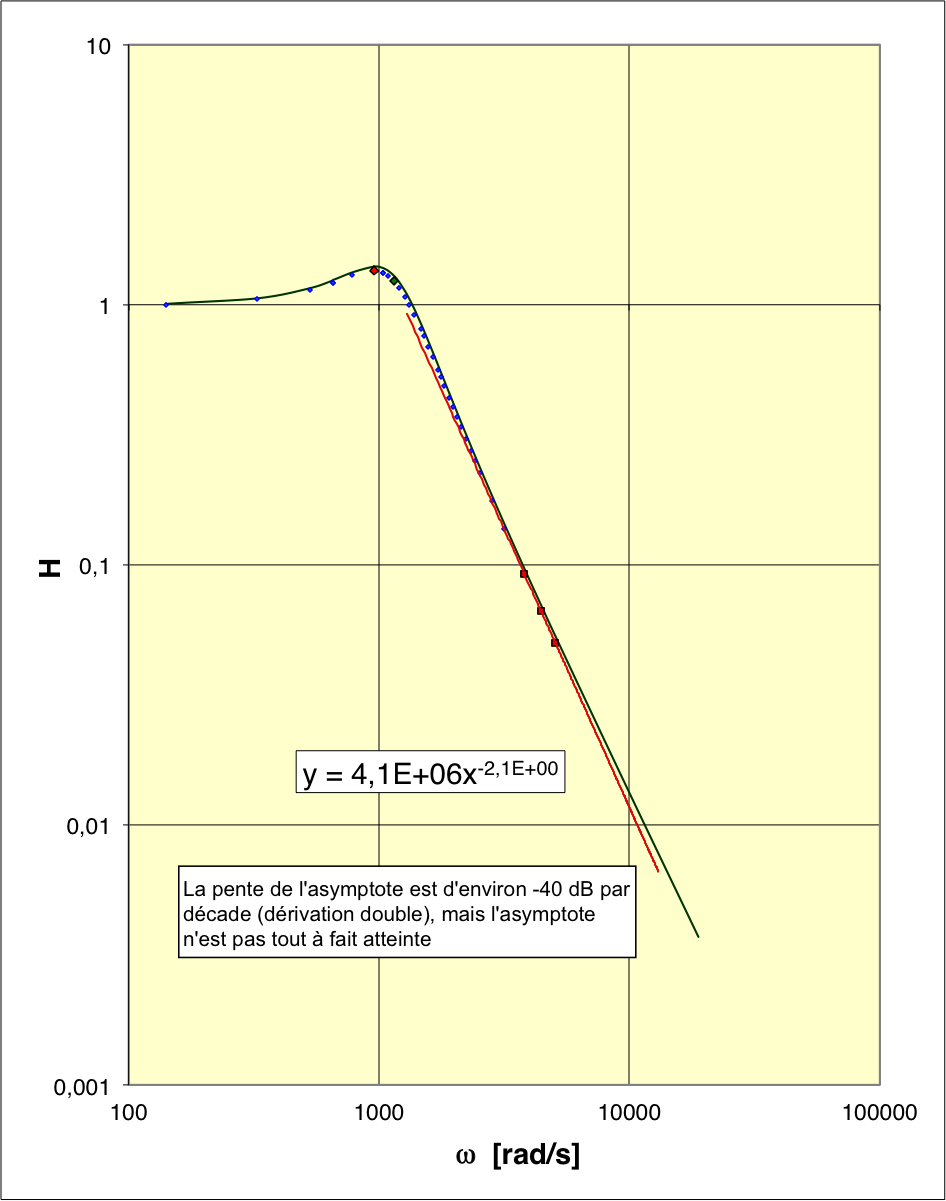
• Le modèle théorique (déduit du cours pour les valeurs choisies des composants RLC) représente plutôt correctement les données (en vert) ; il est intéressant de comparer à la modélisation simplifiée négligeant

r

(en marron) dont la représentation est seulement légèrement moins bonne (

r≪R_0

Le gain peut s'écrire

\displaystyle H=\frac{\sqrt{r^2+(Lω)^2}}{\sqrt{R^2+\left(Lω-\frac{1}{Cω}\right)^2}}

; en négligeant

r

pour éviter de compliquer inutilement, le maximum correspond au minimum de

\displaystyle \frac{R^2}{L^2 ω^2}+\left(1-\frac{1}{LCω^2}\right)^2

. Avec

\displaystyle w=\frac{ω_0^{\:2}}{ω^2}

\displaystyle κ=\frac{R^2}{L^2 ω_0^{\:2}}

la dérivée de

κ \:w +(1-w)^2

s'annule pour

\displaystyle w=1-\frac{κ}{2}

; ceci correspond à :

\displaystyle ω_r=\frac{ω_0}{\sqrt{1-\frac{1}{2} \frac{R^2}{L^2 ω_0^{\:2}}}}>ω_0

.

On obtient ici :

\displaystyle ω_0=\frac{1}{\sqrt{L \,C}}=3433±75 \:\mathrm{rad.s^{-1}}

;

\displaystyle \frac{1}{2} \frac{R^2}{L^2 ω_0^{\:2}}=1,07>1

;

ω_r^{\:2}<0

;

H_{max}=1

.

Les pulsations de coupure correspondent à :

ω_1≈3650±50 \:\mathrm{rad.s^{-1}}

ω_2≈∞

(avant de devenir imaginaire

ω_r→∞

et il n'y a pas de coupure supérieure). La bande passante est donc :

∆ω=∞

; on ne peut pas comparer à

\displaystyle \frac{R}{L}=5030±95 \:\mathrm{rad.s^{-1}}

(valable pour la sortie aux bornes de la résistance) puisqu'il n'y a pas de résonance.

Le facteur de qualité est

\displaystyle 𝒬=\frac{ω_0}{∆ω}=0

(

𝒬≪1

correspond à une résonance quasi-inexistante).

• De façon analogue au cas de la sortie aux bornes du condensateur, on obtient ici tout de même une résonance pour

ϕ(ω)

, bien qu'elle soit nettement moins marquée (bascule de phase plus progressive).

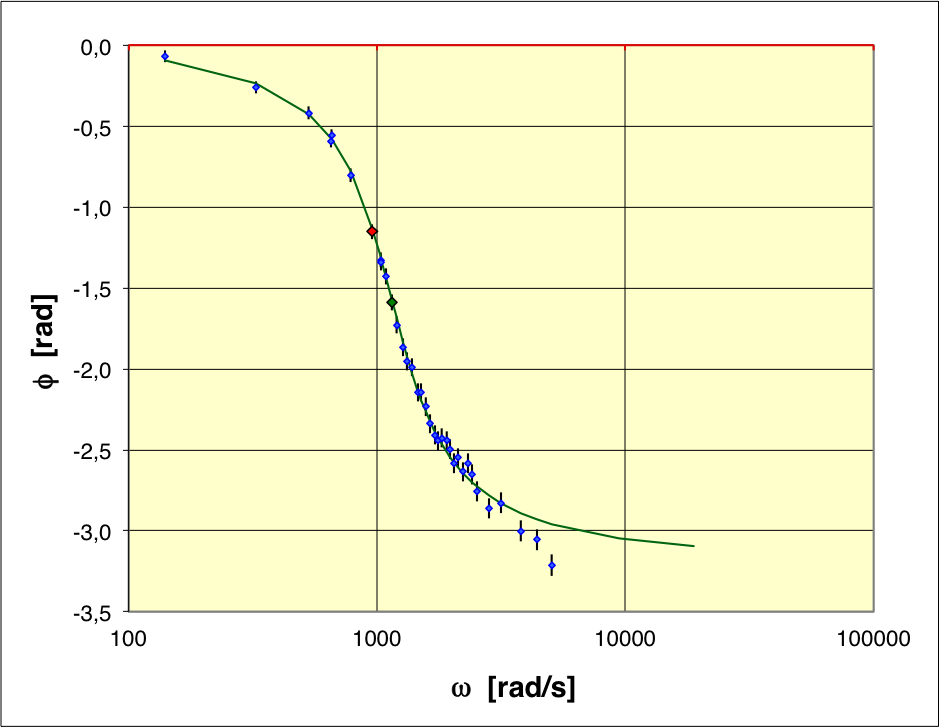
• Le déphasage peut s'écrire

\displaystyle ϕ=\arctan\left(\frac{Lω}{r}\right)-\arctan\left(\frac{Lω-\frac{1}{Cω}}{R}\right)

; ce modèle modèle théorique représente plutôt correctement les données (en vert). Il est par contre intéressant de comparer à la modélisation simplifiée négligeant

r

(en marron) dont la représentation est nettement moins bonne pour les premiers points : à cause de

r

ϕ→\frac{π}{2}

aux très basses fréquences (le modèle simplifié donne la limite

π

). Le passage par

ϕ=\frac{π}{2}

est en accord avec

ω_0

.

Les pulsations de coupure sont définies autrement pour le déphasage ; la coupure supérieure pour

ϕ=\frac{π}{4}

est

ω_2=6710±40 \:\mathrm{rad.s^{-1}}

; la coupure inférieure pour

ϕ=\frac{3 \,π}{4}

est

ω_1=1540±60 \:\mathrm{rad.s^{-1}}

(un peu perturbée par l'effet de

r

) ; la bande passante est :

∆ω=5170±100 \:\mathrm{rad.s^{-1}}

compatible avec

\displaystyle \frac{R}{L}

(cette définition par le déphasage est sur ce point plus pratique).

Cela correspond à un facteur de qualité

\displaystyle 𝒬=\frac{ω_0}{∆ω}=\text{0,66}±{0,03}

(

𝒬≪1

correspond à une résonance très peu marquée).

◊ remarque : en réalité, la résistance de la bobine augmente avec la fréquence (surtout si la bobine contient un noyau) ; ceci est dû aux interactions électromagnétiques dans les spires de la bobine (qui font qu'à haute fréquence le courant ne circule qu'en surface des fils : effet de peau), ainsi qu'aux courants induits dans le noyau ; les modèles simples utilisés ici sont imparfaits, mais il sont raisonnablement satisfaisants.

4. Influences de R et C

4.1. Sortie aux bornes de la résistance $R_0$

• Puisque les modélisations proposées décrivent correctement les mesures, il est plus simple d'utiliser les variations des courbes théoriques sous l'effet de divers paramètres.

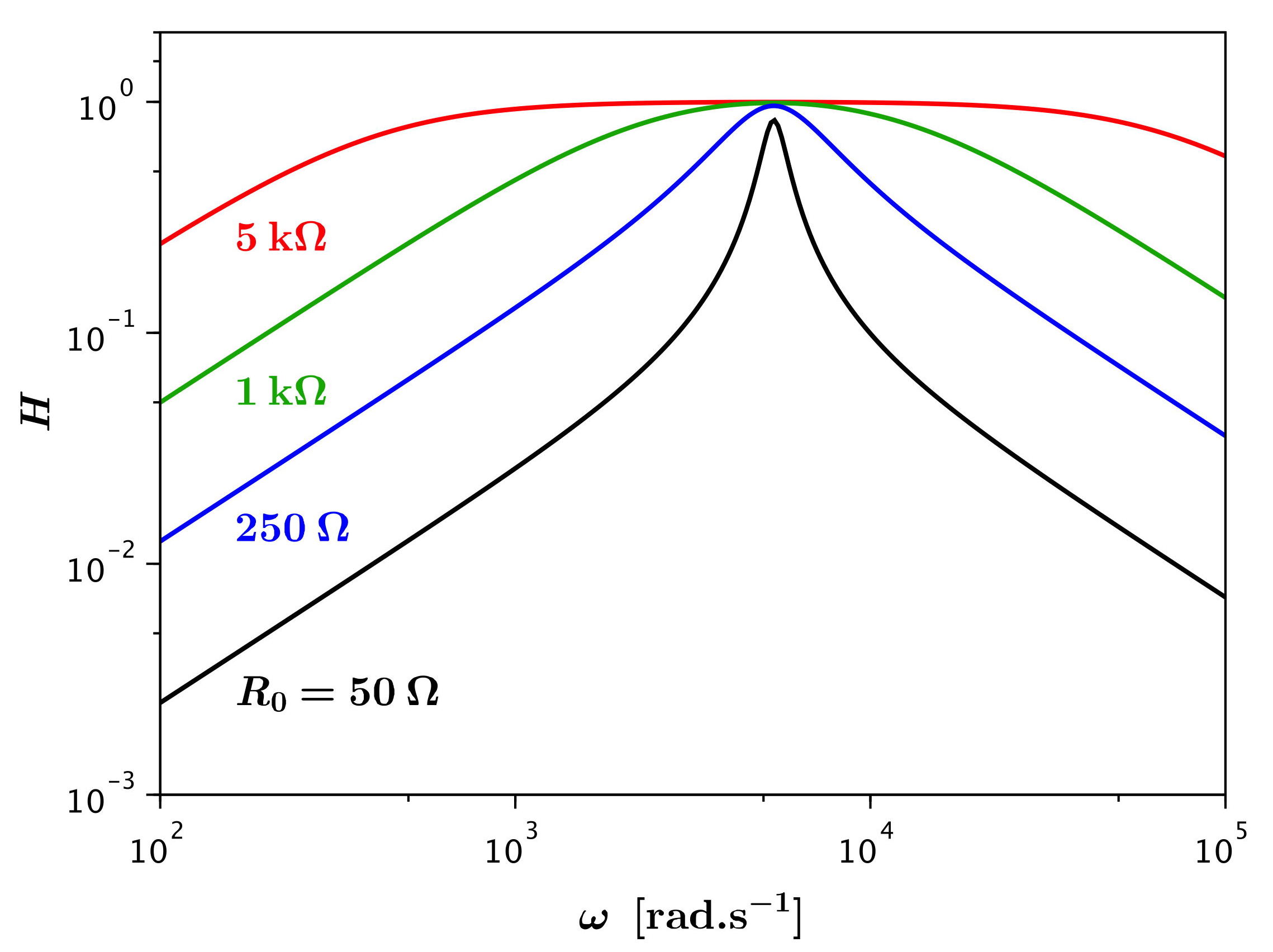
• On peut étudier l'effet de

R_0

(en prenant comme référence, en noir, l'exemple étudié expérimentalement).

D'une part l'augmentation de la résistance totale élargit la résonance car l'amortissement par la réactance aux fréquences extrêmes est en proportion moins important.

D'autre part

r

est de plus en plus négligeable donc le maximum augmente et tend vers

1

.

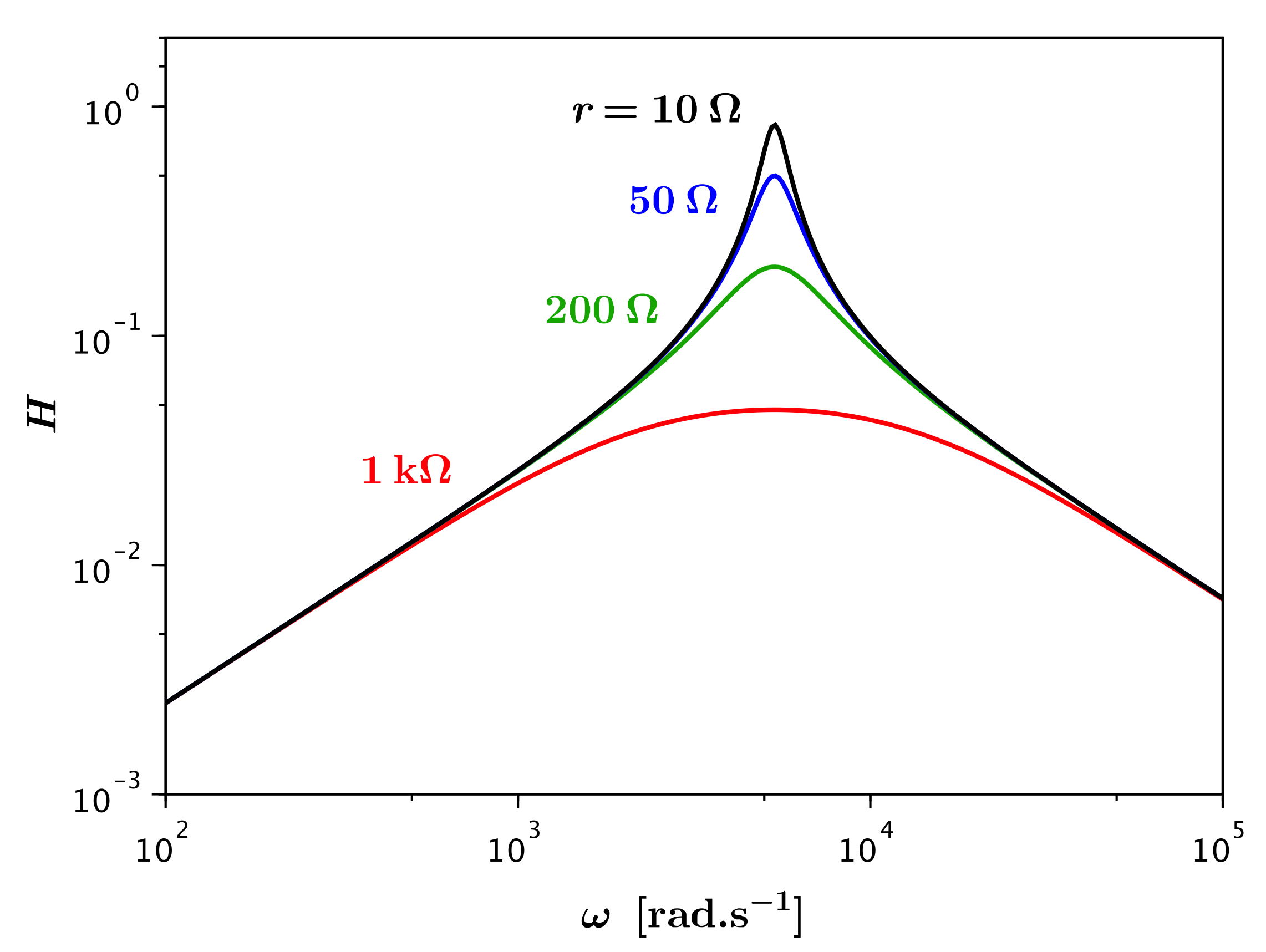
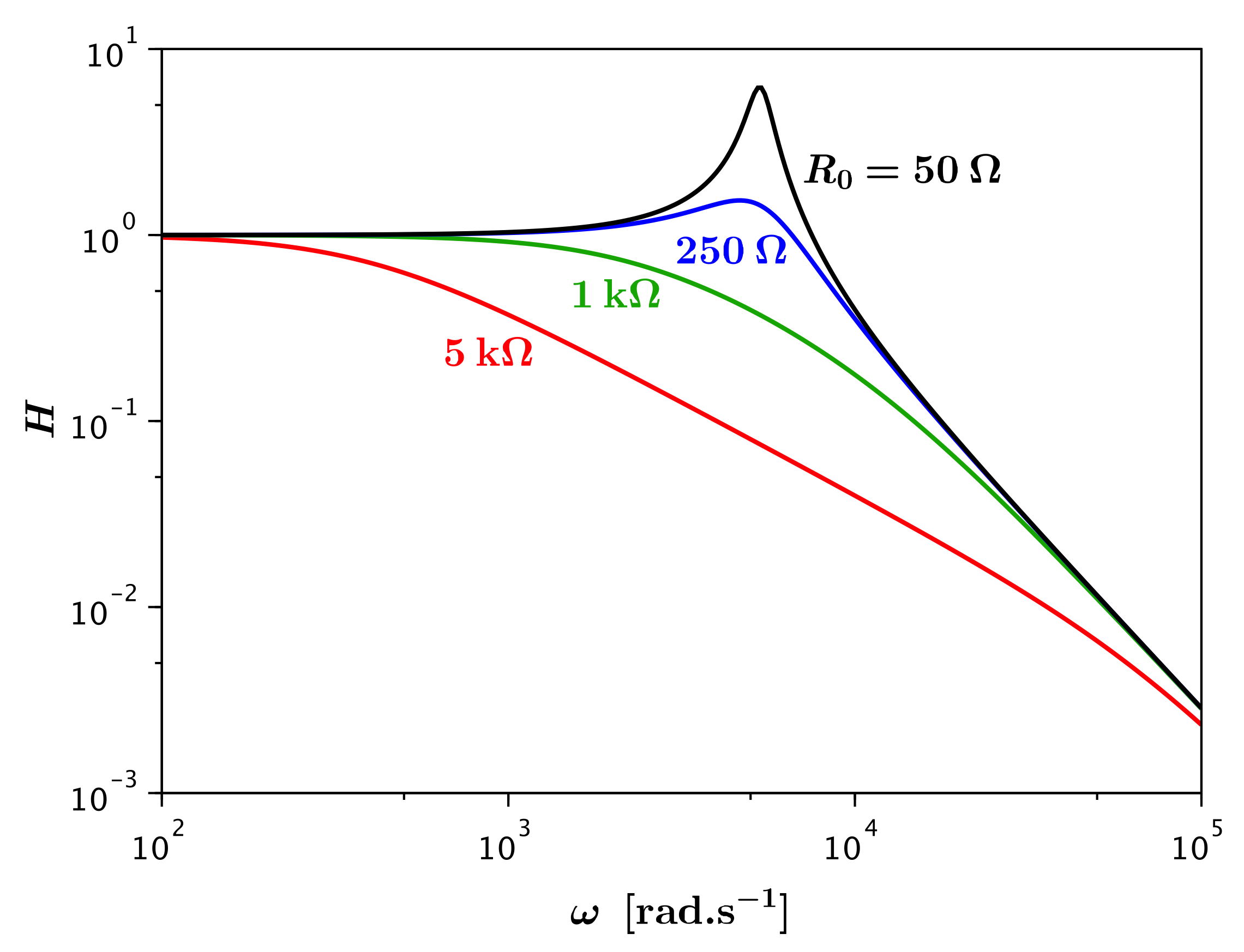
• On peut comparer avec l'effet de

r

De même l'augmentation de la résistance totale élargit la résonance, mais d'autre part

R_0

est en proportion de moins en moins important donc le maximum diminue et tend vers

0

.

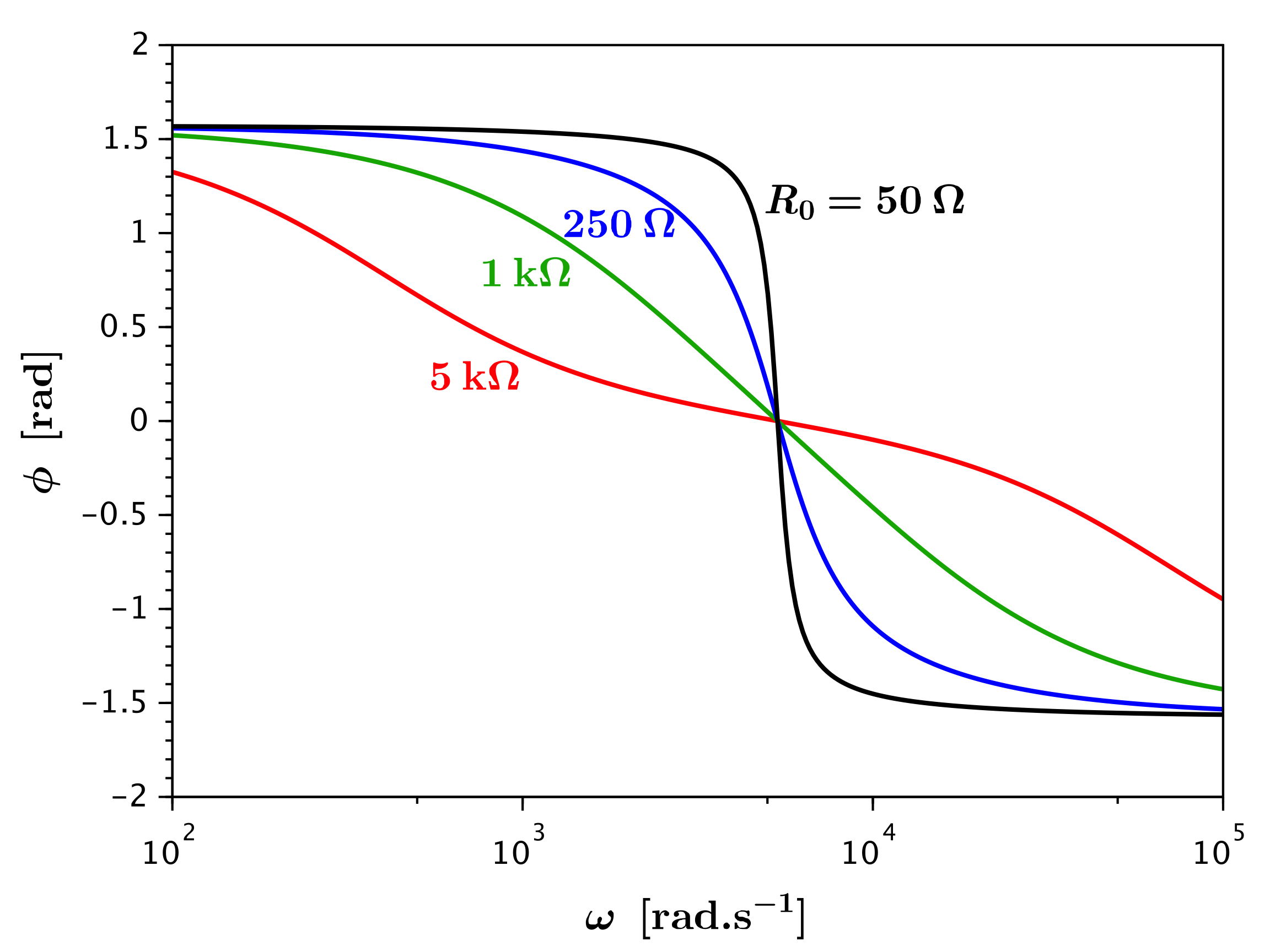
• L'effet sur le déphasage est du même type en augmentant

R_0

r

car

ϕ

ne dépend que de la résistance totale. Il correspond à un saut de phase de plus en plus progressif.

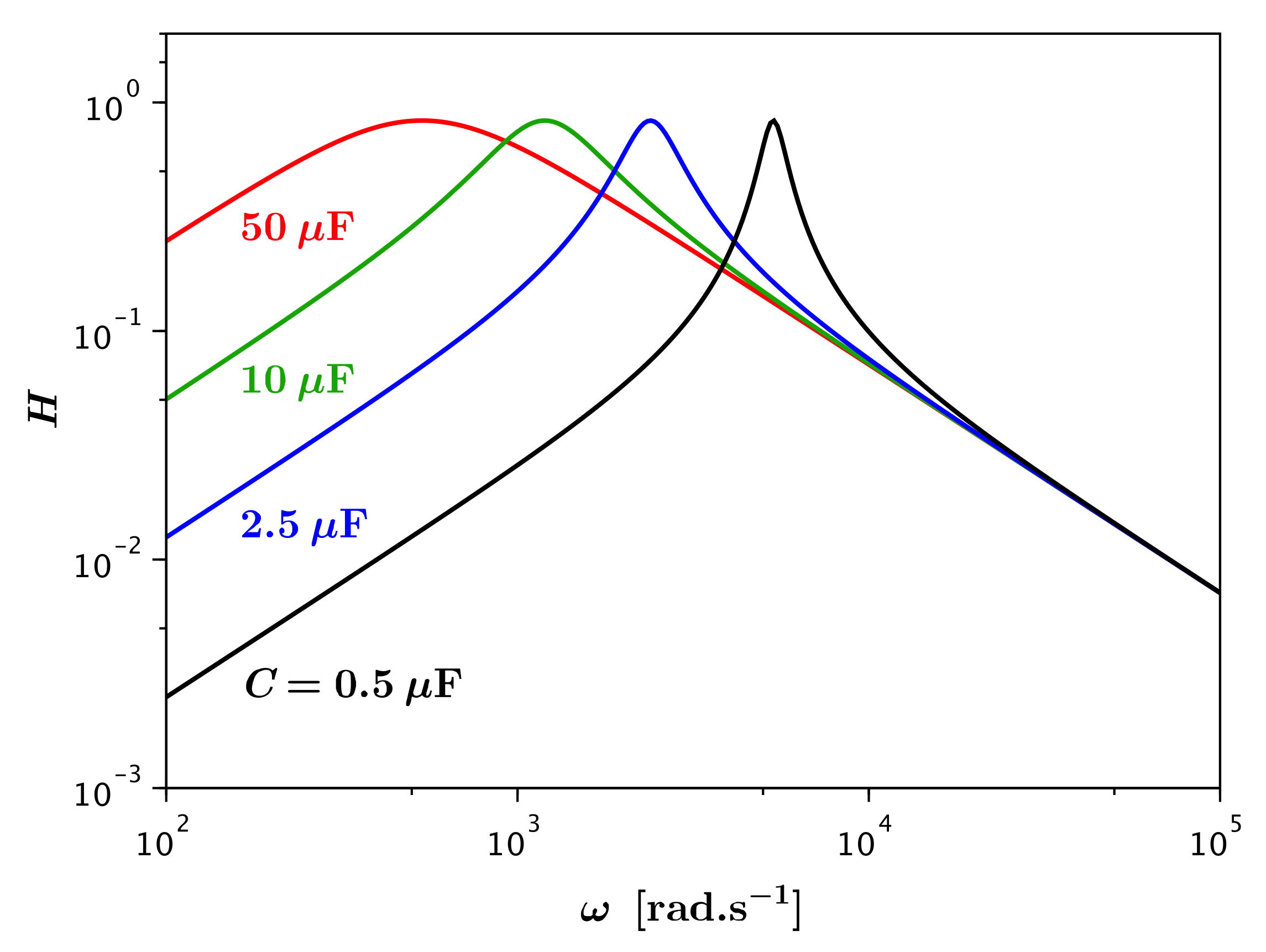
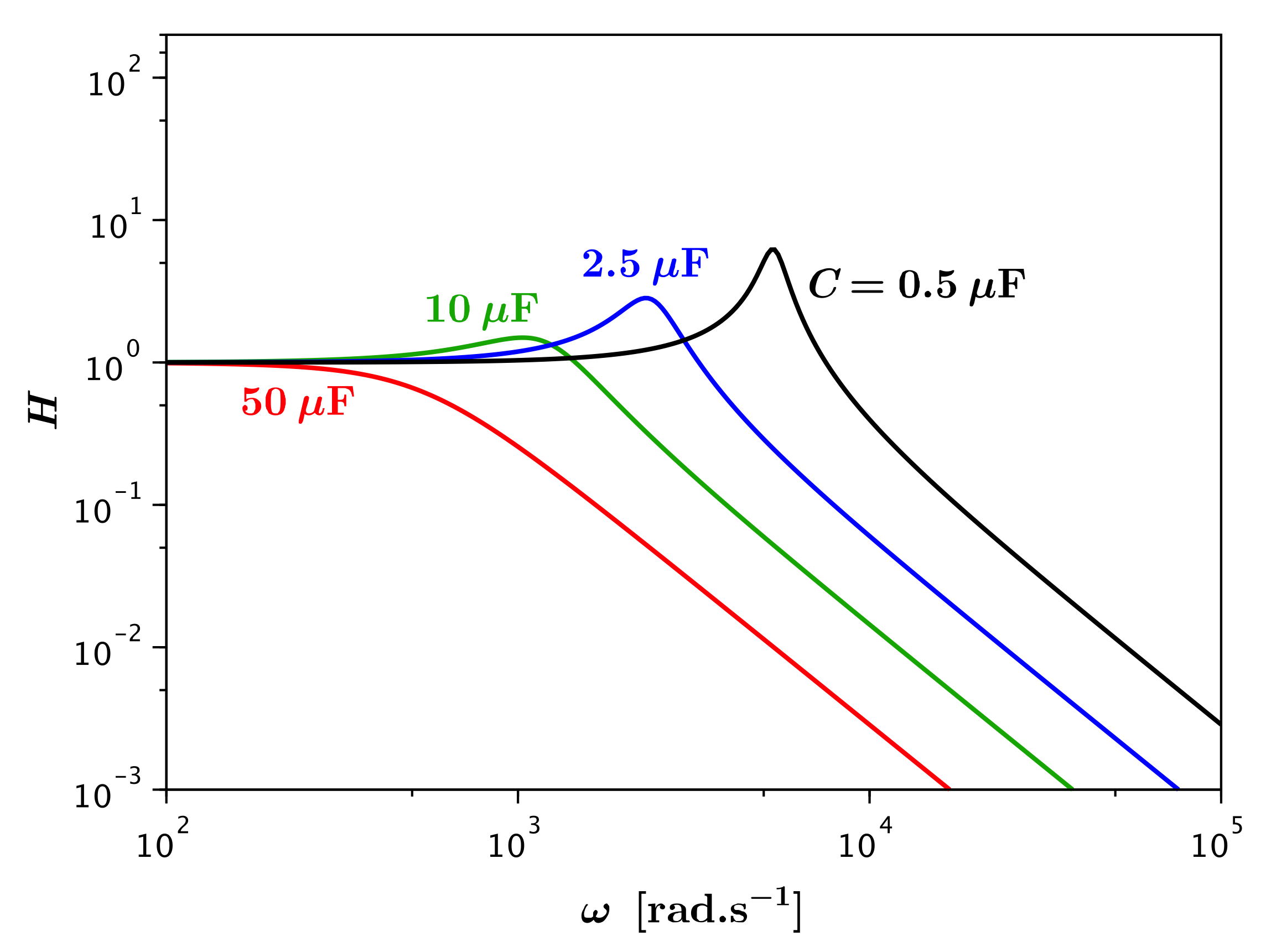
• D'un autre point de vue, on peut étudier l'effet de

C

D'une part l'augmentation de la capacité fait devenir prépondérant le régime capacitif à des fréquences plus faibles : dans la comparaison de

\displaystyle \frac{1}{C \,ω}

R

, un

C

plus grand intervient pour

ω

plus petit.

D'autre part cela élargit la résonance car l'effet de l'inductance aux hautes fréquences est inchangé.

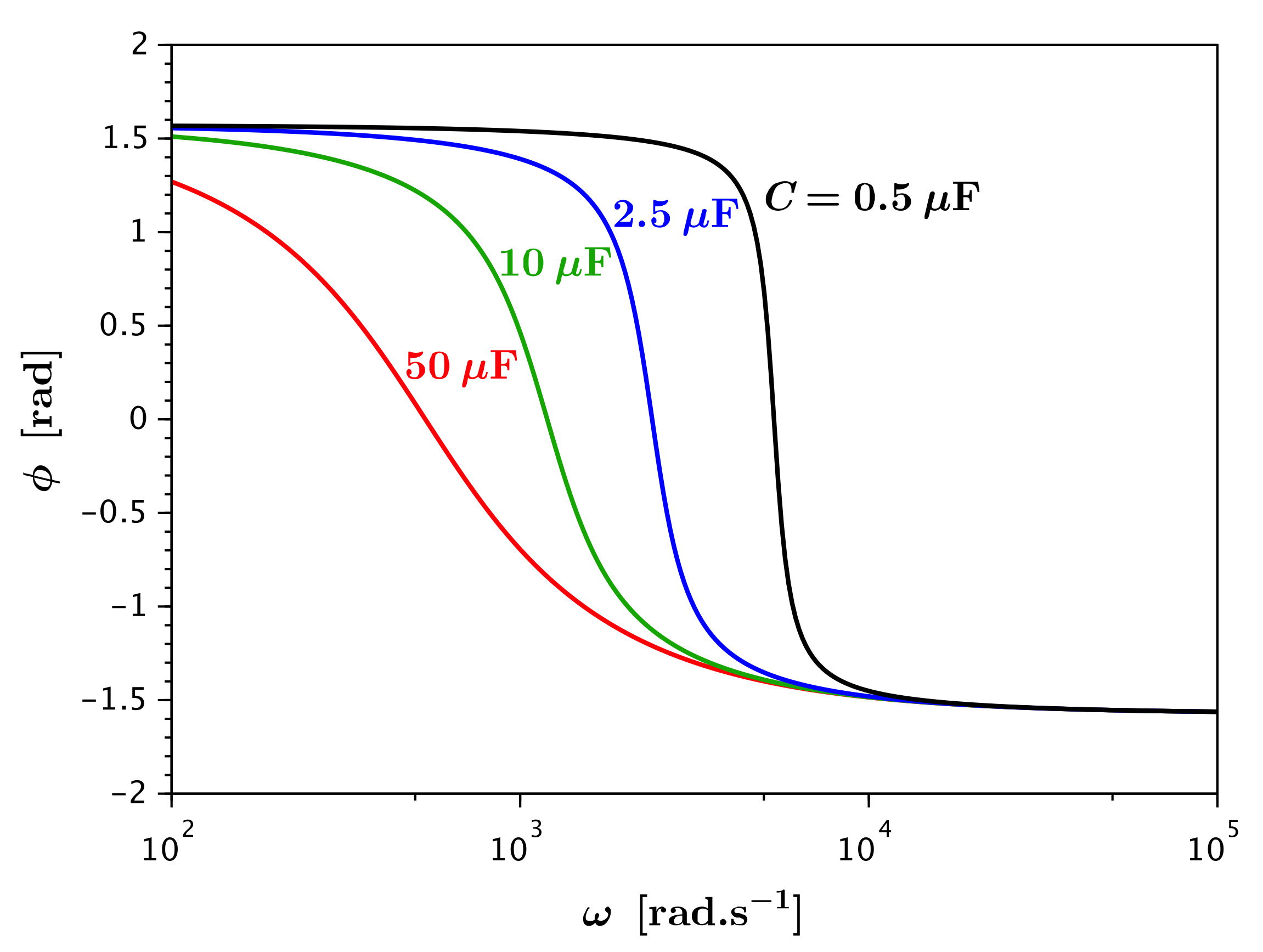
• L'effet sur le déphasage conduit aux mêmes remarques.

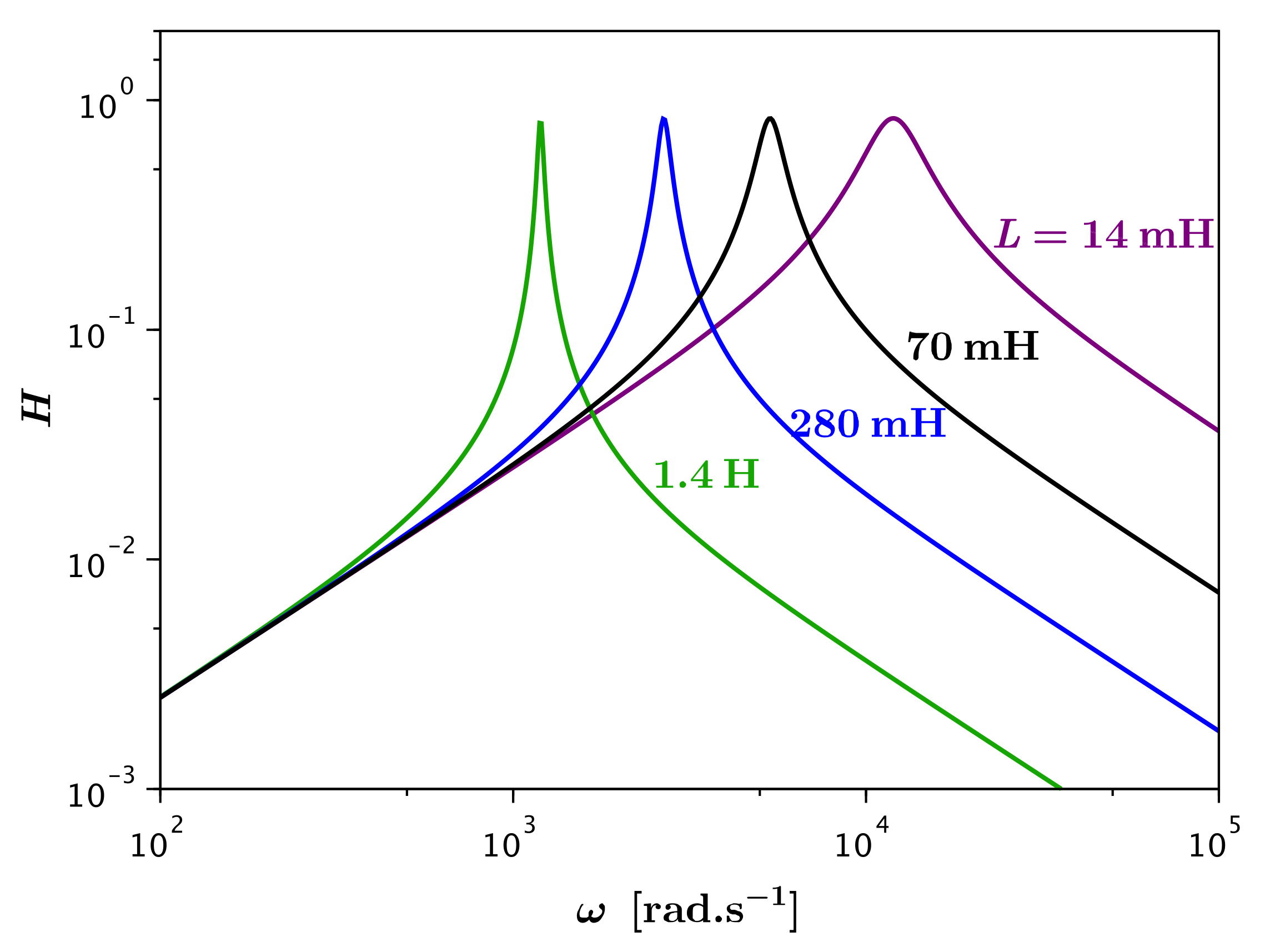
• Puisqu'on se base ici sur les modèles, on peut aussi comparer à l'effet de

L

L'effet est analogue, mais pour l'effet inductif aux hautes fréquences : dans la comparaison de

L \,ω

R

, un

L

plus grand intervient pour

ω

plus petit.

D'autre part cela resserre la résonance car l'effet de la capacité aux basses fréquences est inchangé.

• L'effet sur le déphasage conduit aux mêmes remarques.

4.2. Sortie aux bornes de la capacité

• Puisque le nombre de combinaisons est grand, on n'en cite ici que quelques unes. Pour tout ce qui concerne les déphasages, il y a juste un décalage de

\frac{π}{2}

puisque l'argument de l'impédance du condensateur est constant, comme celui pour la résistance.

• On peut étudier l'effet de

R_0

(l'effet est du même type en augmentant

R_0

r

car

H

ne dépend que de la résistance totale).

D'une part l'augmentation de la résistance totale élargit la résonance (domaine de prépondérance de la résistance) car l'effet de la réactance aux fréquences extrêmes est en proportion moins important.

D'autre part

\displaystyle \frac{1}{C \,ω}

a de moins en moins tendance à rester prépondérant quand la fréquence augmente, donc le maximum diminue et tend vers

1

(prépondérance de la capacité ; la résonance disparaît).

• On peut comparer à l'effet de

C

Ce cas ressemble au précédent : un

C

plus grand diminue l'impédance

\displaystyle \frac{1}{C \,ω}

au détriment de la résistance qui est donc plus facilement prépondérante ; mais la comparaison entre

R

L \,ω

est inchangée donc ceci élargit la résonance seulement du côté capacitif, donc cela la décale vers les basses fréquences.

D'autre part comme pour l'exemple précédent le maximum diminue et tend vers

1

(prépondérance de la capacité ; la résonance disparaît).

4.3. Sortie aux bornes de la bobine

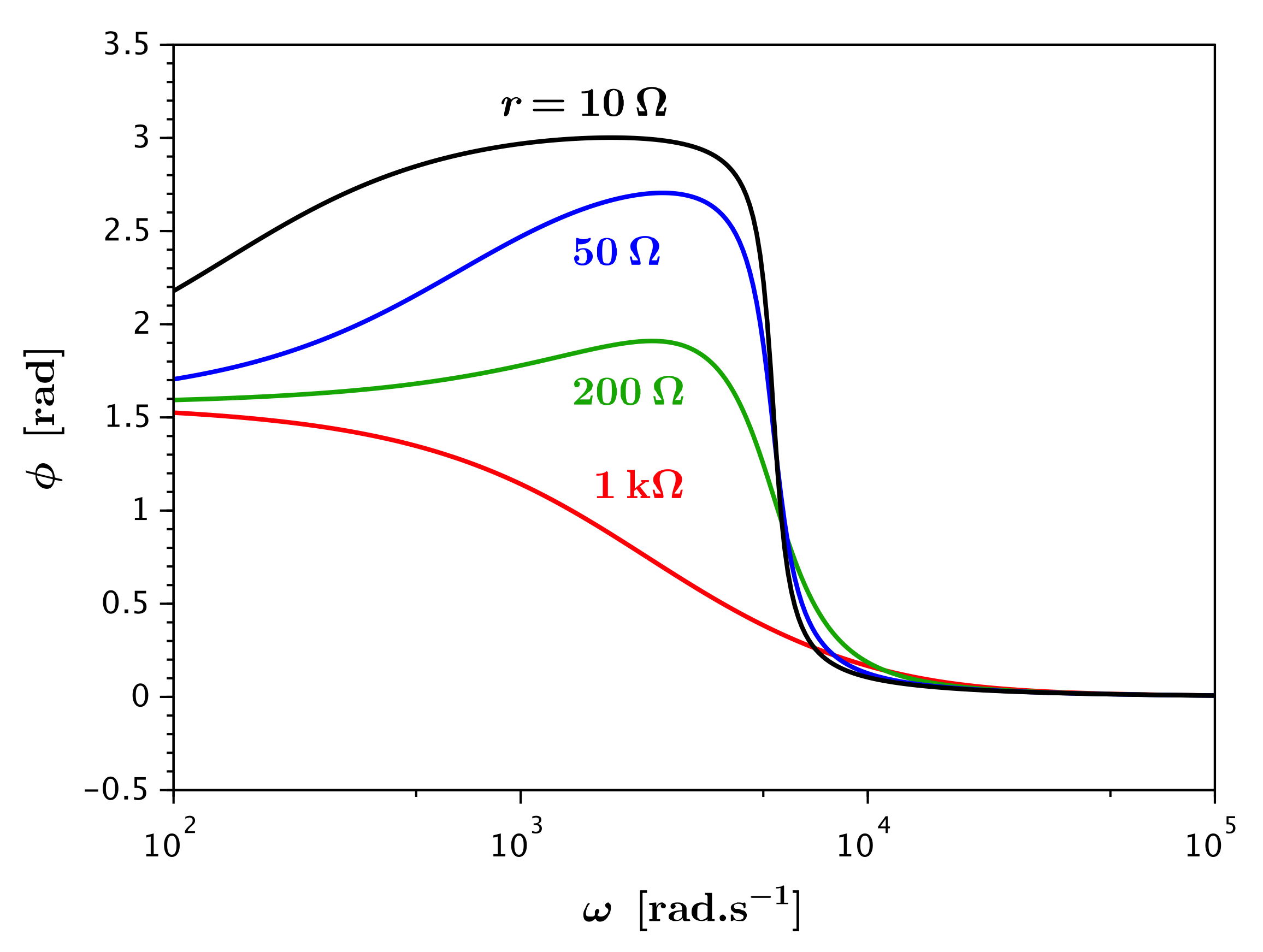
• Cette situation est plus complexe à cause de la résistance de la bobine ; on peut se limiter à un exemple caractéristique : l'effet de

r

sur le déphasage.

Dès les faibles valeurs

r

perturbe aux basses fréquences : l'inductance devient sans effet, on mesure aux bornes d'une “résistance” et on compare au total qui est surtout capacitif, d'où

ϕ≈\frac{π}{2}

. Mais cette perturbation n'affecte que les très basses fréquences et on observe le saut de phase associé à la résonance.

Quand

r

augmente un peu, cela augmente la résistance totale donc le saut de phase devient plus progressif. Mais si

r

devient très grand, alors on n'observe même plus de résonance.