EC.IV - RÉGIMES TRANSITOIRES - CIRCUITS RL ET RC

1. Courants “lentement variables”

• Les lois de Kirchhoff (et de nombreux corollaires) sont encore valables dans la limite où les courants et tensions électriques varient “lentement” : durées caractéristiques supérieures à la nanoseconde pour les conducteurs usuels.

• On note généralement par des minuscules (

u

i

, ...) les grandeurs variables (même si la dépendance

u(t)

i(t)

... n'est pas indiquée explicitement) ; on note au contraire par des majuscules (

U

I

, ...) les grandeurs constantes.

2. Circuits inductifs

2.1. Notion d'inductance

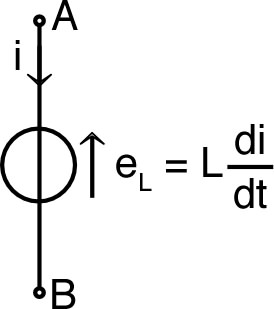
• Là où interviennent des phénomènes magnétiques variables, le champ électrique ne dérive pas d’un potentiel ; il faut alors ajouter des tensions proportionnelles aux dérivées des effets magnétiques.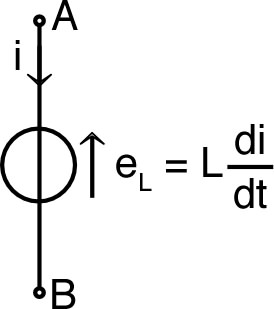

Dans une bobine idéale, cela cause une f.c.e.m. proportionnelle à la dérivée du courant :

\displaystyle u_L (t)=\frac{dϕ}{dt}=L\:\frac{di}{dt}

; le coefficient

L

est nommé “inductance”.

☞ remarque : on n'utilise pas le symbole de Thévenin, car les lois d'association ne se généralisent pas aux tensions dépendant non de

i

mais de

\displaystyle \frac{di}{dt}

• En électrocinétique, les inductances sont en général obtenues sous formes de “bobines”, possédant en plus une résistance (pour une inductance non négligeable, il faut un fil long, donc mince, donc assez résistif).

◊ remarque : pour obtenir une inductance qui ne soit pas trop petite, en évitant d'utiliser une bobine trop grande, on y ajoute généralement un “noyau” ferromagnétique ; en première approximation, cela multiplie l'inductance par ≈ 100, mais la proportionnalité entre

e_L

\displaystyle \frac{di}{dt}

n'est plus exactement vérifiée (et devient même nettement fausse pour des tensions trop grandes).

2.2. Aspects énergétiques

• Du point de vue énergétique, la puissance reçue correspond à la variation d'énergie magnétique (

\frac{1}{2} L \:i^2

) :

\displaystyle 𝒫=u_{AB} \:i=L \:i \:\frac{di}{dt}=\frac{d}{dt} \left(\frac{1}{2} L \:i^2 \right)

.

Cette puissance ne pouvant pas être infinie, l’énergie magnétique doit varier de façon continue ; il en est de même pour le courant qui traverse la bobine.

2.3. Associations d'inductances

• La relation caractéristique des inductances est “linéaire” (au sens des équations différentielles).

On en déduit que les inductances en série s'ajoutent :

L=L_1+L_2+L_3

\displaystyle u_{AD}=u_{AB}+u_{BC}+u_{CD}=L_1 \:\frac{di}{dt}+L_2 \:\frac{di}{dt}+L_3 \:\frac{di}{dt}=(L_1+L_2+L_3) \:\frac{di}{dt}

• De façon réciproque, en parallèle les inverses des inductances s'ajoutent (mais il n'y a pas de notation “à la Norton” simple) :

\displaystyle \frac{di}{dt}=\frac{di_1}{dt}+\frac{di_2}{dt}+\frac{di_3}{dt}=\frac{u}{L_1} +\frac{u}{L_2} +\frac{u}{L_3} =\left(\frac{1}{L_1} +\frac{1}{L_2} +\frac{1}{L_3} \right) \;u=\frac{u}{L}

3. Circuit “RL”

• Pour un circuit RL (en série) soumis à un échelon de tension, la loi des mailles s'écrit :

\displaystyle R \:i+L \:\frac{di}{dt}=e(t)

Ceci peut aussi s'écrire :

\displaystyle i +τ \:\frac{di}{dt}=i_c (t)

avec

\displaystyle i_c (t)=\frac{e(t)}{R}

et où

\displaystyle τ=\frac{L}{R}

est appelé “constante de temps” du circuit RL.

• Pour chercher les solutions d'une équation différentielle linéaire, on peut utiliser le fait que la différence de deux solutions est solution d'une équation simplifiée (dite “homogène”) dont le second membre est nul.

Ainsi, la solution générale de l'équation complète peut être calculée comme la somme :

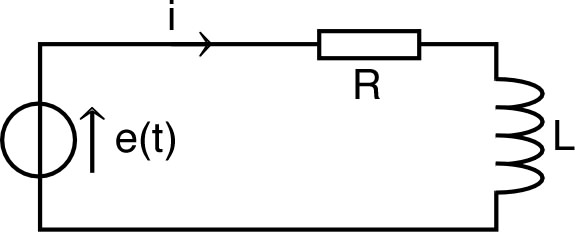◊	d'une solution particulière de l'équation complète ;
◊	de la solution générale de l'équation homogène.

Le circuit étant soumis à un échelon de tension :

e(t)=E

E'

est “constante par morceaux” ; on peut donc chercher une solution particulière constante par morceaux. On vérifie alors que

i(t)=i_c (t)

est solution (pour chaque morceau).

En ce qui concerne l'équation homogène, on cherche des solutions de même forme que leurs dérivées (pour obtenir un total nul) ; on peut les chercher sous la forme exponentielle

I_0 \mathrm{e}^{r \:t}

(avec

I_0=Cte

r=Cte

dans

ℝ

ℂ

). On aboutit alors à l'équation caractéristique :

1+τ \:r=0

donc

\displaystyle r=-\frac{1}{τ}

.

• Pour

t≤0

, la solution est de la forme :

i(t)=A \:\mathrm{e}^{-t/τ}+I

avec

\displaystyle I=\frac{E}{R}

; mais la seule solution physiquement acceptable est :

\displaystyle i(t)=I=\frac{E}{R}

constant.

Pour

t≥0

, la solution est de la forme :

i(t)=A' \:\mathrm{e}^{-t/τ}+I'

avec

\displaystyle I'=\frac{E'}{R}

; donc d'après les conditions initiales (par continuité) :

i(t)=(I-I') \:\mathrm{e}^{-t/τ}+I'

• La tension aux bornes de “l'inductance” est :

\displaystyle u_L=L \:\frac{di}{dt}=(E'-E) \:\mathrm{e}^{-t/τ}

mais elle est rarement observable ainsi car on ne peut généralement pas négliger la résistance de la bobine.

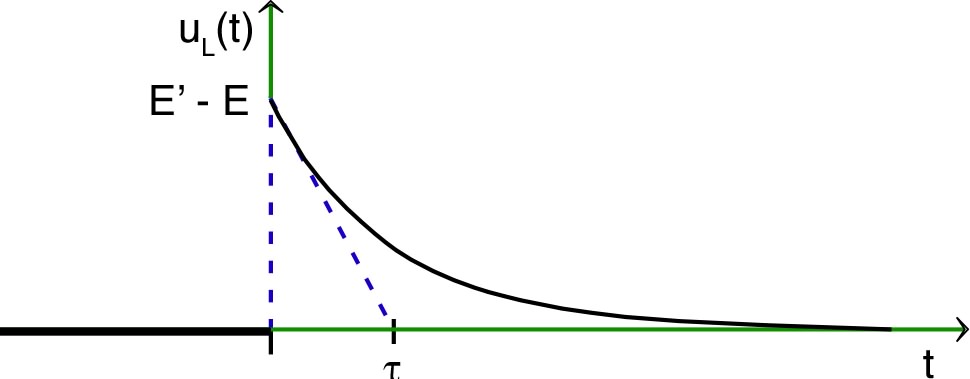
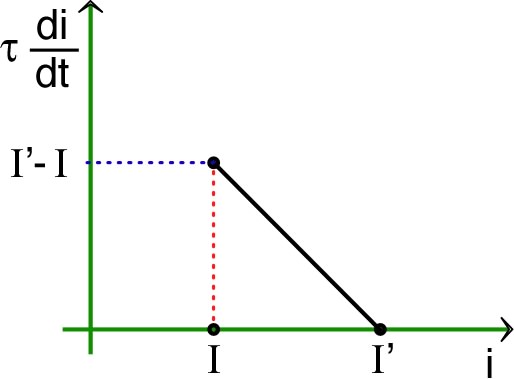
◊ remarque : on peut aussi caractériser l'évolution du système par un diagramme dans “l'espace des phases”

\displaystyle \left(i \:;τ \:\frac{di}{dt}\right)

.

📖 exercice n° I.

4. Circuits capacitifs

4.1. Notion de capacité

• Un condensateur peut accumuler une charge

q

proportionnelle à la tension entre ses bornes :

q=C \:u_C

; le coefficient

C

est nommé “capacité”.

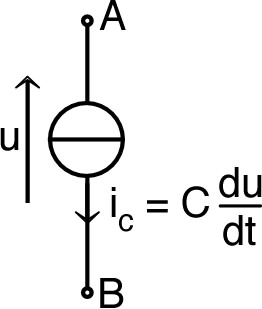Ceci lui permet de générer un courant, tel que :

\displaystyle i_c=C \:\frac{du}{dt}

.

☞ remarque : on n'utilise pas le symbole de Norton, car les lois d'association ne se généralisent pas aux courants dépendant non de

u

mais de

\displaystyle \frac{du}{dt}

◊ remarque : la “charge totale” du condensateur est nulle ; la charge du côté où arrive le courant est liée à celui-ci par la relation :

\displaystyle i=\frac{dq}{dt}

, mais il y a une charge opposée de l’autre côté.

4.2. Aspects énergétiques

• Du point de vue énergétique, la puissance reçue correspond à la variation d'énergie électrostatique (

\frac{1}{2} C \:u_{AB}^{\;2}

) :

\displaystyle 𝒫=u_{AB} \:i=C \:u_{AB} \,\frac{du_{AB}}{dt}=\frac{d}{dt} \left(\frac{1}{2} C \:u_{AB}^{\;2} \right)

.

Cette puissance ne pouvant pas être infinie, l’énergie électrostatique doit varier de façon continue ; il en est de même pour la charge du condensateur et pour la tension entre ses bornes.

4.3. Associations de capacités

• La relation caractéristique des capacités est “linéaire” (au sens des équations différentielles).

On en déduit que les capacités en parallèle s'ajoutent :

C=C_1+C_2+C_3

\displaystyle i=i_1+i_2+i_3=C_1 \,\frac{du}{dt}+C_2 \,\frac{du}{dt}+C_3 \,\frac{du}{dt}=(C_1+C_2+C_3) \:\frac{du}{dt}

• De façon réciproque, en série les inverses des capacités s'ajoutent (mais il n'y a pas de notation “à la Thévenin” simple) :

\displaystyle \frac{du}{dt}=\frac{du_1}{dt}+\frac{du_2}{dt}+\frac{du_3}{dt}=\frac{i}{C_1} +\frac{i}{C_2} +\frac{i}{C_3} =\left(\frac{1}{C_1} +\frac{1}{C_2} +\frac{1}{C_3} \right) \:i=\frac{i}{C}

5. Circuit “RC”

• Pour un circuit RC (en série) soumis à un échelon de tension, la loi des mailles peut s'écrire :

\displaystyle R \:i+\frac{1}{C} ∫ \,i(t) \:dt=e(t)

Ceci peut aussi s'écrire :

\displaystyle τ \:\frac{du}{dt}+u=e(t)

avec

u=u_C

(pour simplifier) et où

τ=R\,C

est appelé “constante de temps” du circuit RC.

• Pour

t≤0

, la solution est donc de la forme :

u(t)=A \:\mathrm{e}^{-t/τ}+E

; mais la seule solution physiquement acceptable est :

u(t)=E

constant.

Pour

t≥0

, la solution est donc de la forme :

u(t)=A' \:\mathrm{e}^{-t/τ}+E'

; donc d'après les conditions initiales (par continuité) :

u_C (t)=(E-E') \:\mathrm{e}^{-t/τ}+E'

• Le courant de charge du condensateur de capacité

C

est alors de la forme :

\displaystyle i(t)=C \:\frac{du_C}{dt}=\frac{e(t)-u_C}{R}=(I'-I) \:\mathrm{e}^{-t/τ}

avec

\displaystyle I'=\frac{E'}{R}

\displaystyle I=\frac{E}{R}

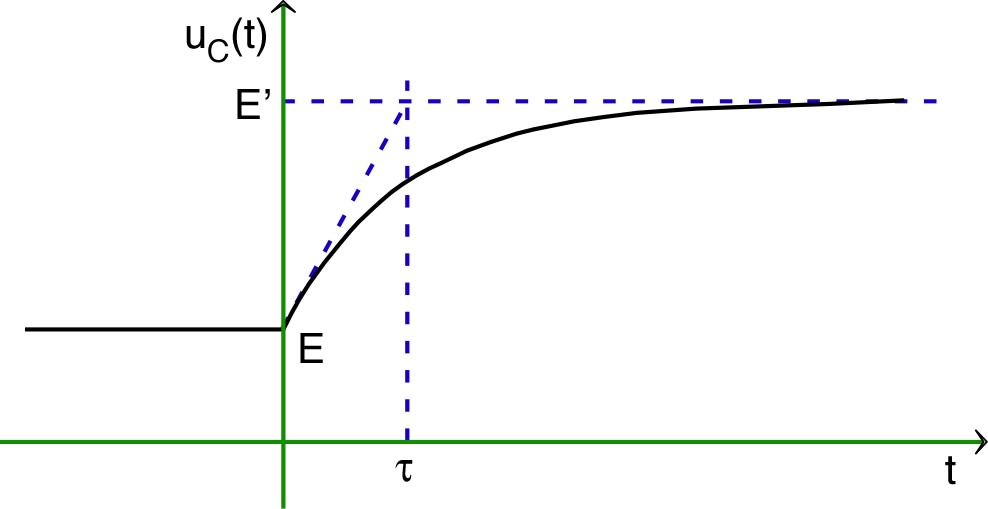
◊ remarque : on peut aussi caractériser l'évolution du système par un diagramme dans “l'espace des phases”

\displaystyle \left(u \,;τ \frac{du}{dt}\right)

.

📖 exercices n° II, III, IV, V et VI.

6. Transformée de Laplace

• La solution générale de l'équation :

\displaystyle τ \:\frac{du}{dt}+u=e(t)

pour

e(t)

quelconque peut être obtenue par variation de la constante

A

dans la solution

A \:\mathrm{e}^{-t/τ}

de l'équation homogène :

\displaystyle \frac{dA(t)}{dt}=\frac{1}{τ}\:\mathrm{e}^{-t/τ} \:e(t)

;

\displaystyle A(t)=\frac{1}{τ} \,∫ \,e(t) \:\mathrm{e}^{t/τ} \:dt+Cste

;

\displaystyle u(t)=u(t_0) .\mathrm{e}^{(t_0-t)/τ}+\frac{1}{τ} \,∫_{t_0}^t \,e(t') \:\mathrm{e}^{(t'-t)/τ} \:dt'

Ainsi, si on connaît la réponse transitoire à un échelon, on peut calculer la réponse stationnaire à tout signal.

◊ remarque : de même qu'on peut approcher toute fonction par une somme de fonctions sinusoïdales (décomposition de Fourier), on peut aussi le faire par une somme de fonctions en échelon.

• La forme de la solution obtenue suggère que, si on sait calculer les intégrales du type

F(p)=∫_0^∞ \,f(t) \:\mathrm{e}^{-p t} \:dt=ℒ\{f(t)\}

(“transformée de Laplace” pour

t≥0

), on peut en déduire les solutions de toutes les équation différentielles linéaires.

Avec

ℒ\{\frac{du}{dt}\}=p \:ℒ\{u\}-u(0)

on peut écrire

\displaystyle ℒ\{u\}=\frac{1}{τ \:p+1} .[ℒ\{e(t)\}+τ \:u(0)]

. Par ailleurs

\displaystyle \frac{1}{p+α}=ℒ\{\mathrm{e}^{-α t} \}

donc

\displaystyle ℒ\{u\}=\frac{1}{τ} ℒ\{\mathrm{e}^{-t/τ} \}.ℒ\{e(t)\}+ℒ\{\mathrm{e}^{-t/τ} \}.u(0)

.

Or, pour deux fonctions

f

g

, le produit des transformées de Laplace est la transformée du produit de convolution :

[f*g](t) =∫_{-∞}^∞ \,f(t').g(t-t') \:dt'

; on en déduit inversement :

\displaystyle u(t)=u(0) .\mathrm{e}^{-t/τ}+\frac{1}{τ} \,∫_0^t \:e(t') \:\mathrm{e}^{(t'-t)/τ} \:dt'

.

◊ remarque : cette transformée de Laplace tient ici (pour les régimes transitoires) un rôle analogue à celui de la transformée de Fourier dans l'étude des régimes sinusoïdaux (ces deux approches ne sont pas indépendantes).