• La première relation donne . La seconde peut s’écrire ; les solutions sont de la forme : avec ; les conditions initiales (courant raisonnablement nul) imposent : .
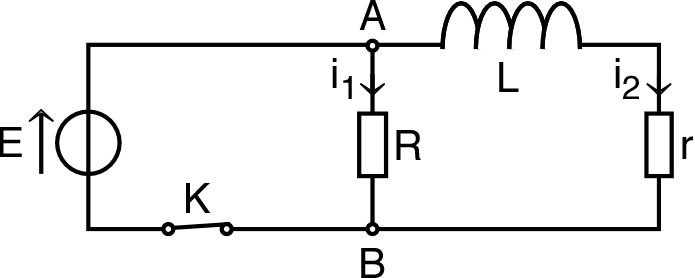
| 1. | • Lorsqu’on ferme l’interrupteur, il apparaît
des courants
et
tels que : . • La première relation donne . La seconde peut s’écrire ; les solutions sont de la forme : avec ; les conditions initiales (courant raisonnablement nul) imposent : . |
| 2. | • Après un temps assez long (),
on peut supposer que la limite est atteinte :
; on ouvre alors l’interrupteur :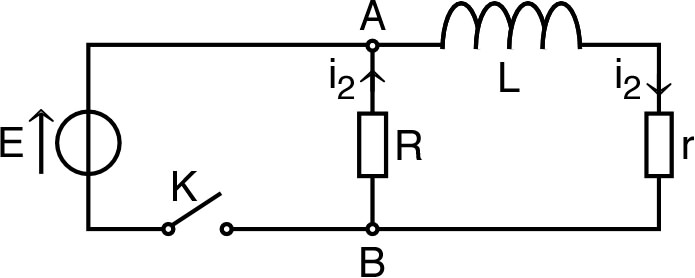 • Les courants et sont alors tels que : et . Cette équation peut s’écrire ; les solutions sont de la forme : avec ; les conditions initiales imposent : . • On en déduit la tension : . Cette tension est d’autant plus rapidement décroissante que la résistance est grande, dans la mesure où est d’autant plus petit ; mais la valeur initiale : peut être alors très supérieure à si . |
| 1. | • La loi caractéristique d'une inductance
peut s'écrire :
. Pour un assemblage de deux inductances en série,
donc parcourues par le même courant, l'addition des tensions
correspond à :
|
| 2. | • La loi caractéristique d'une capacité peut
s'écrire :
. Pour un assemblage de deux capacités en parallèle,
donc soumises à une même tension, l'addition des courants
correspond à :
|
| 1.a. | • La loi des nœuds impose : . |
| 1.b. | • La loi des mailles impose :
. • La combinaison des équations précédentes donne : . • Puisque l'énoncé n'indique aucune manipulation ayant pu faire apparaître un courant dans le circuit pour , le courant y est normalement nul (il n'y a que des dipôles récepteurs). |
| 1.c. | • Pour
,
la solution de l'équation différentielle est de la forme
:
avec une constante de temps :
. La situation étant invariante pour tout
,
la seule solution possible est :
. On en déduit par conséquent : . • Pour , la solution de l'équation différentielle est de la forme : et les conditions initiales imposent : . On en déduit alors : . |
| 1.d. | • L'allure des variations du courant i est la
suivante :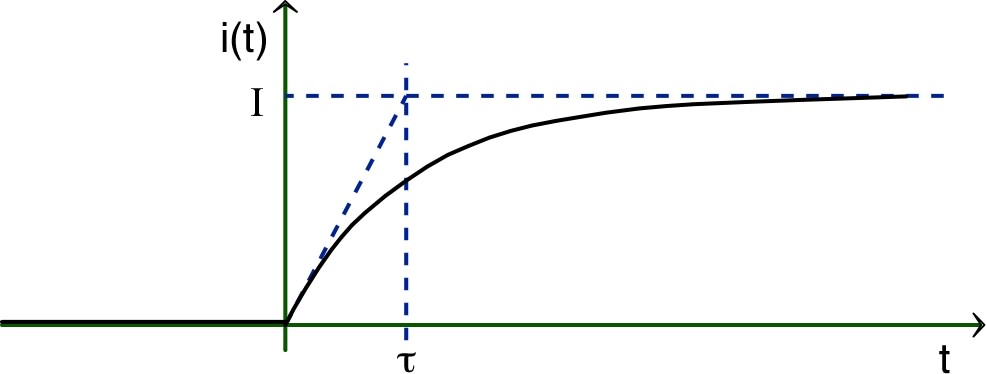 • L'allure des variations du courant est la suivante : 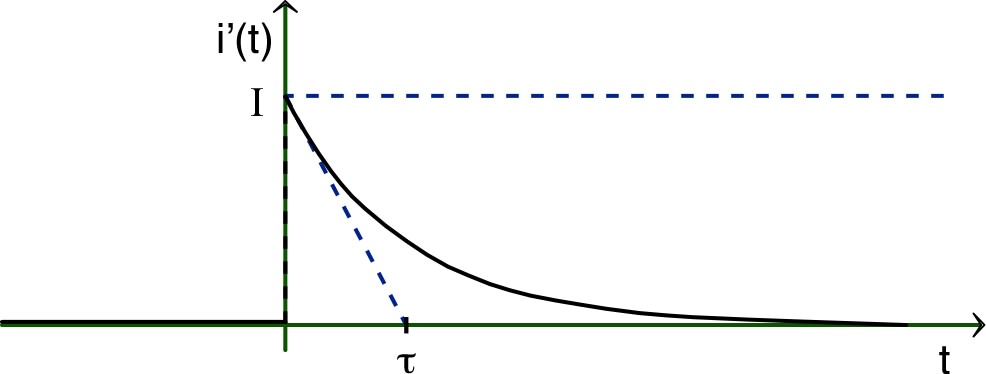 |
| 2.a. |
• La loi des nœuds impose :
. • La loi des mailles impose : . • La charge du condensateur impose : . |
| 2.b. | • La combinaison des équations précédentes
donne : .
Pour
,
cela correspond à : ;
pour
,
cela correspond à : . • Puisque l'énoncé n'indique aucune manipulation ayant pu faire apparaître une charge du condensateur pour , la charge y est normalement nulle (il n'y a que des dipôles récepteurs). |
| 2.c. | • Pour
,
la solution de l'équation différentielle est de la forme
:
avec une constante de temps :
. La situation étant invariante pour tout
,
la seule solution possible est :
. On en déduit par conséquent :
et
. • Pour , la solution de l'équation différentielle est de la forme : et les conditions initiales imposent : . On en déduit : et . |
| 2.d. | • L'allure des variations de la charge est
la suivante (et les variations de
sont semblables, à un coefficient de proportionnalité près).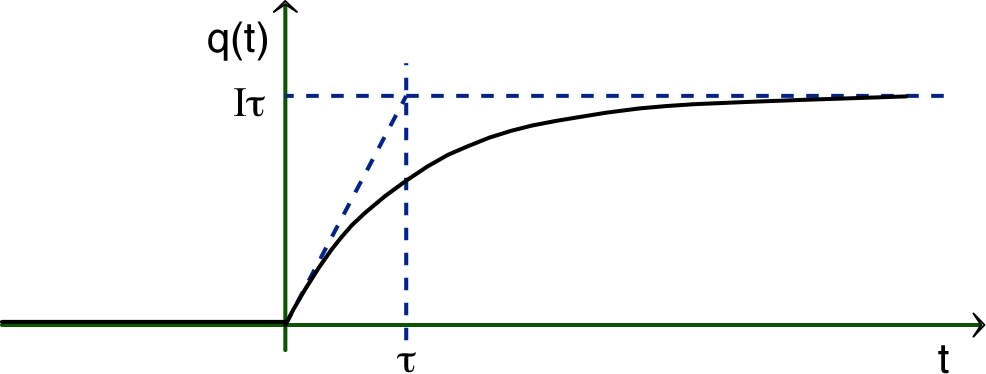 • L'allure des variations du courant est la suivante. 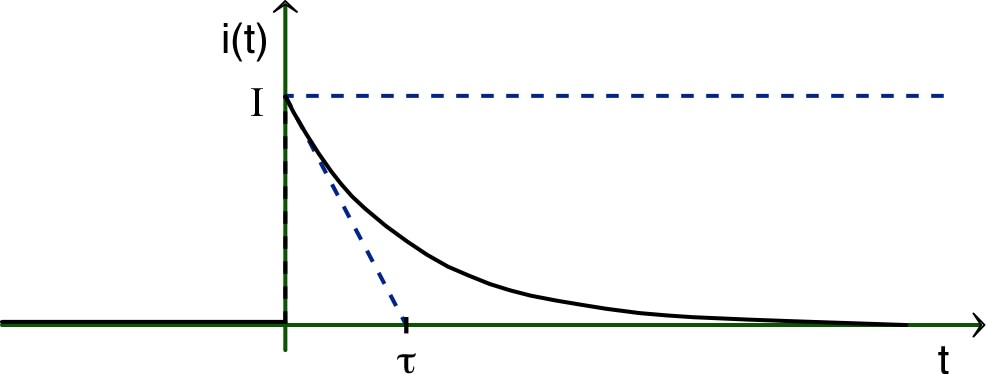 |
| 1.a. | • Pour considérer le signal comme une impulsion de tension, il faut : où est la constante de temps caractéristique du circuit RC. |
| 1.b. | • Pour
,
la loi des mailles
donne l'équation différentielle : .
L'invariance du système pour tout
correspond à :
et . • Pour , l'équation différentielle s'écrit : . Les solutions sont de la forme : et les conditions initiales imposent : . Ainsi : . • Pour , l'équation différentielle : a des solutions de la forme : et les conditions initiales imposent : . Ainsi : . • L'allure des variations de la charge est la suivante. 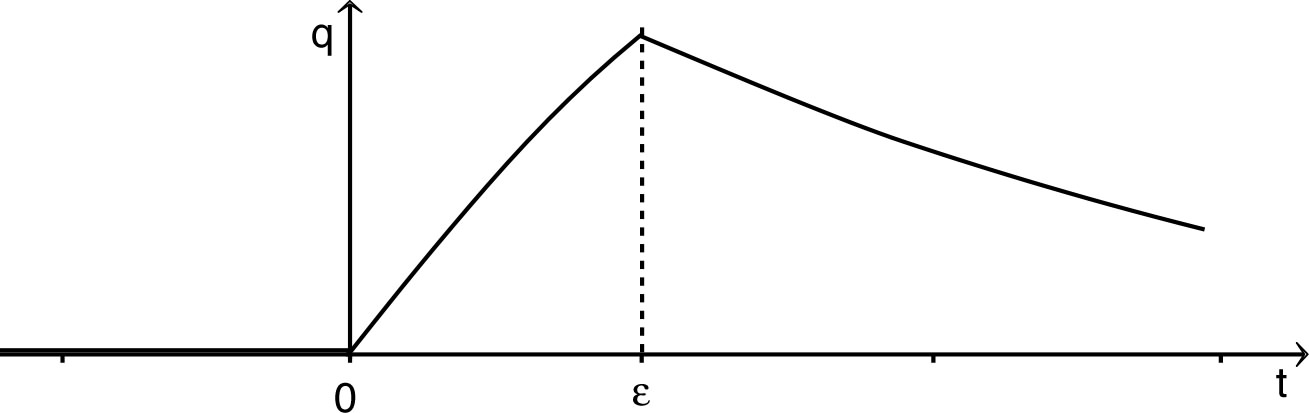 • L'allure des variations du courant est la suivante. 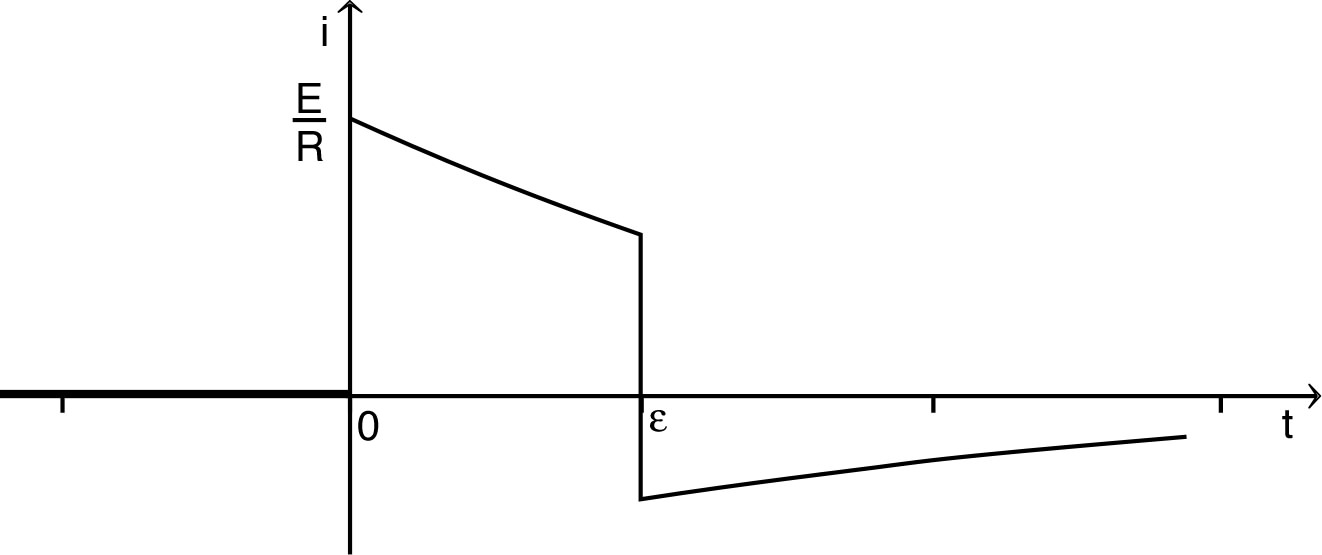 |
| 1.c. | • Pour
,
la limite
correspond à :
et
. • Pour , la limite correspond à : sur des durées d'un l'ordre de grandeur nettement inférieur à ; par suite : ( ) . • L'allure des variations de la charge est la suivante. 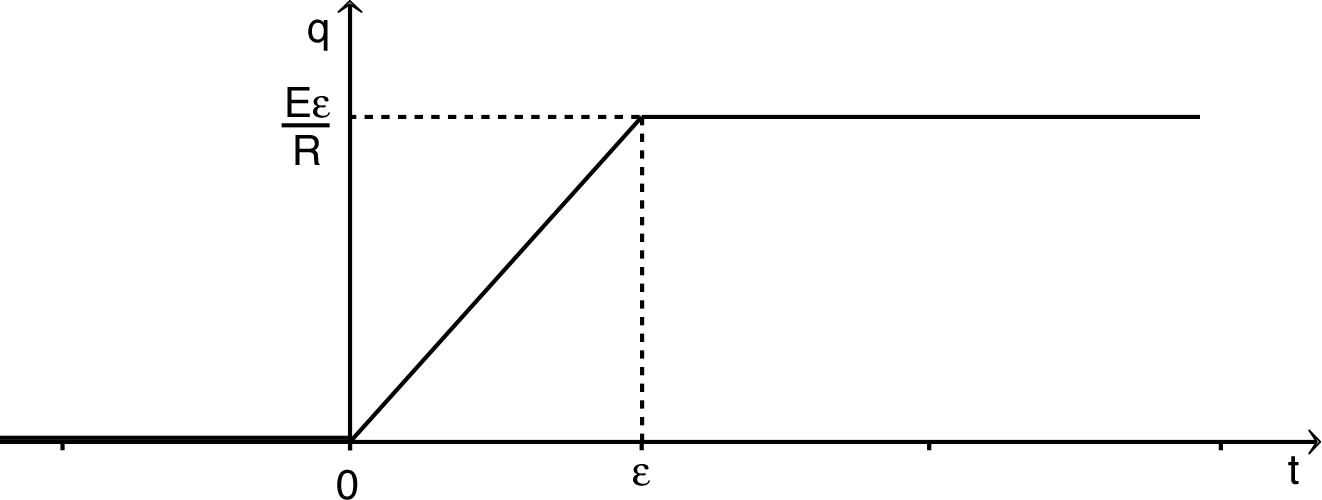 • L'allure des variations du courant est la suivante. 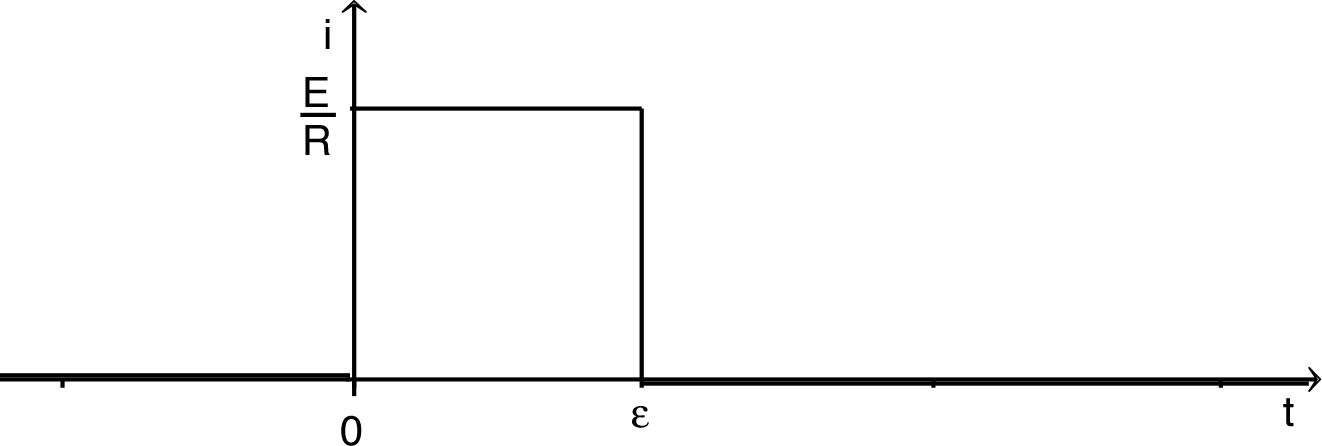 |
| 2.a. | • Pour considérer le signal comme une impulsion de tension, il faut : où est la constante de temps caractéristique du circuit RL. |
| 2.b. | • Pour
,
la loi des mailles conduit à l'équation différentielle
:
. L'invariance du système pour tout
correspond à : . • Pour , l'équation différentielle : a pour solutions : et les conditions initiales imposent : . • Pour , l'équation différentielle s'écrit : . Les solutions sont de la forme : et les conditions initiales imposent : . • L'allure des variations du courant est la suivante. 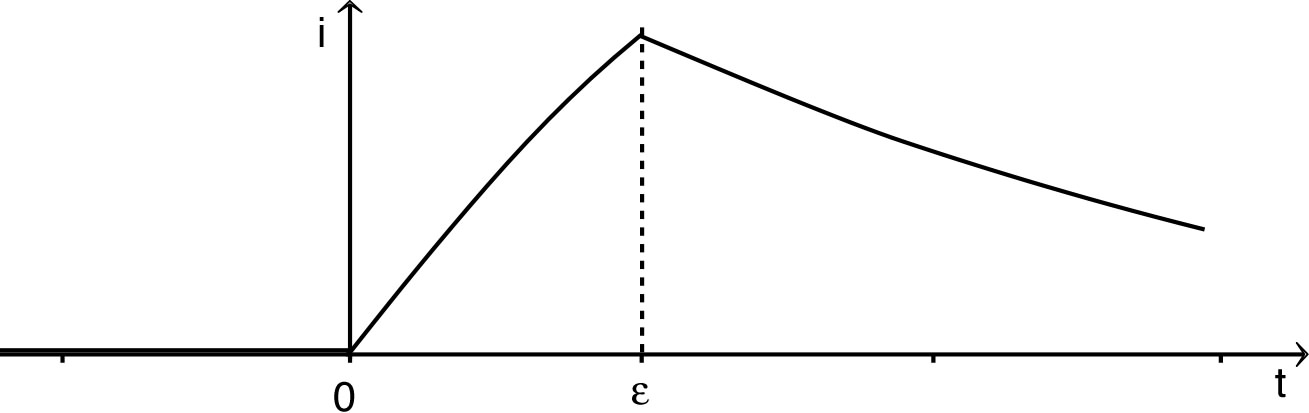 |
| 2.c. | • Pour
,
la limite
correspond à :
. • Pour , la limite donne : pour des durées nettement inférieures à . • L'allure des variations du courant est la suivante. 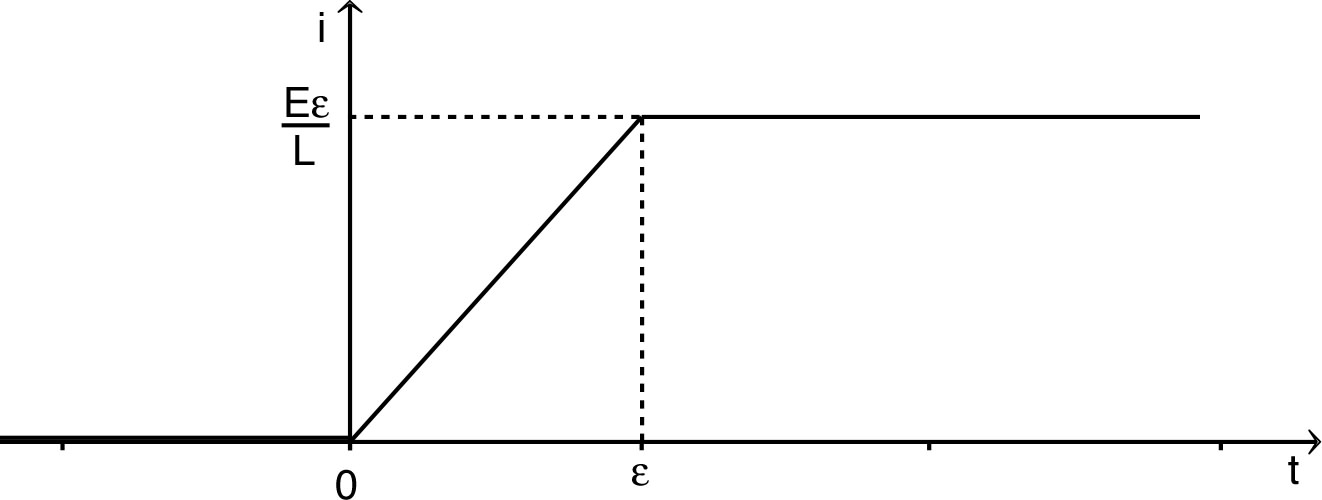 |
| 1.a. | • Pour considérer le signal comme une impulsion de courant, il faut : où est la constante de temps caractéristique du circuit RC. |
| 1.b. | • Pour
,
implique
et la loi des mailles
donne l'équation différentielle : .
L'invariance du système pour tout
correspond à :
et . • Pour , la loi des nœuds donne avec et ; l'équation différentielle s'écrit donc : . Les solutions sont de la forme : et les conditions initiales imposent : . On en déduit alors : . • Pour , l'équation différentielle : a des solutions de la forme : et les conditions initiales imposent : . On en déduit : . • L'allure des variations de la charge est la suivante. 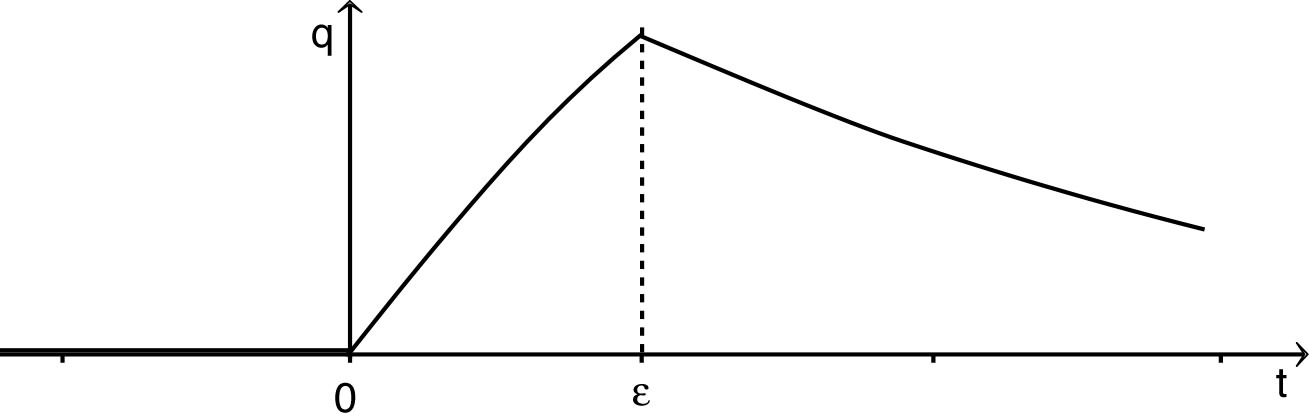 • L'allure des variations du courant est la suivante. 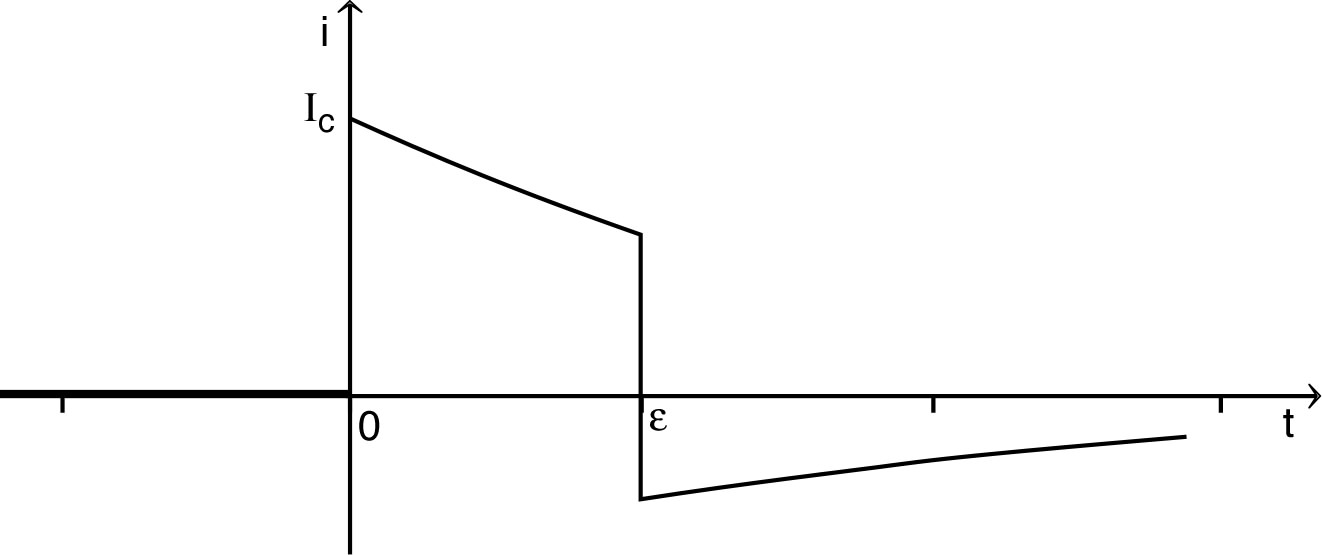 |
| 1.c. | • Pour
,
la limite
correspond à :
et . • Pour , la limite correspond à : sur des durées d'un l'ordre de grandeur nettement inférieur à ; par suite : ( ). • L'allure des variations de la charge est la suivante. 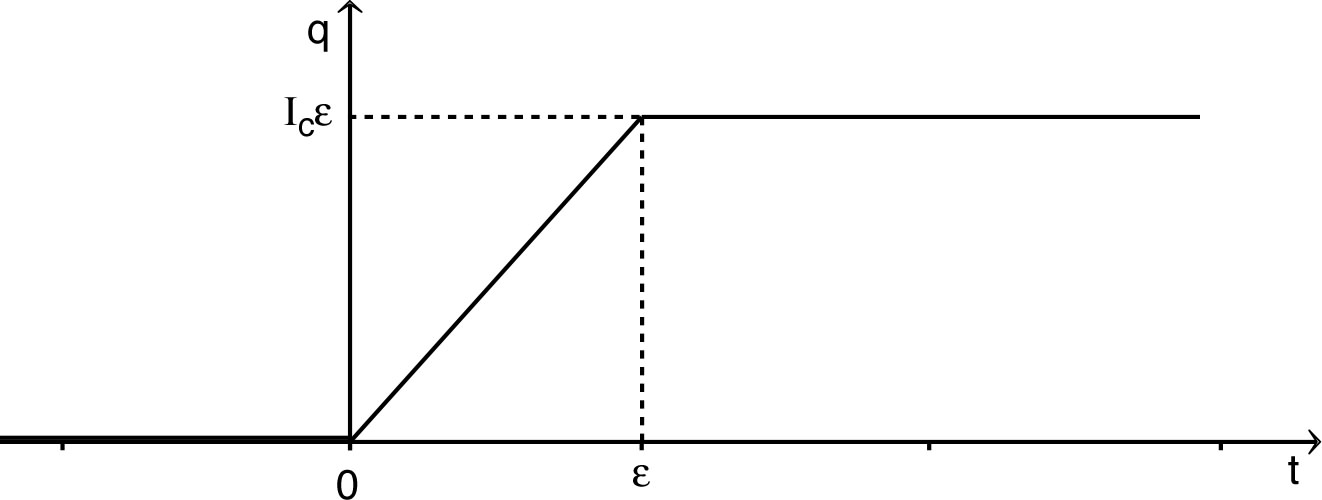 • L'allure des variations du courant est la suivante. 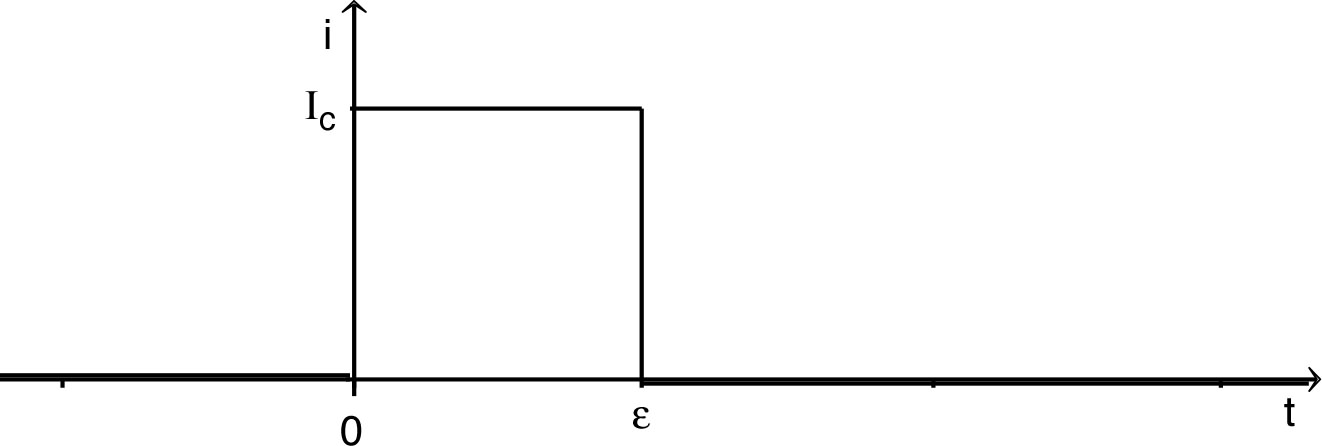 |
| 2.a. | • Pour considérer le signal comme une impulsion de courant, il faut : où est la constante de temps caractéristique du circuit RL. |
| 2.b. | • Pour
,
implique
et la loi des mailles conduit à l'équation différentielle
:
. L'invariance du système pour tout
correspond à : . • Pour , la loi des nœuds donne avec ; l'équation différentielle s'écrit donc : . Les solutions sont de la forme : et les conditions initiales imposent : . • Pour , l'équation différentielle s'écrit : . Les solutions sont de la forme : et les conditions initiales imposent : . • L'allure des variations du courant est la suivante. 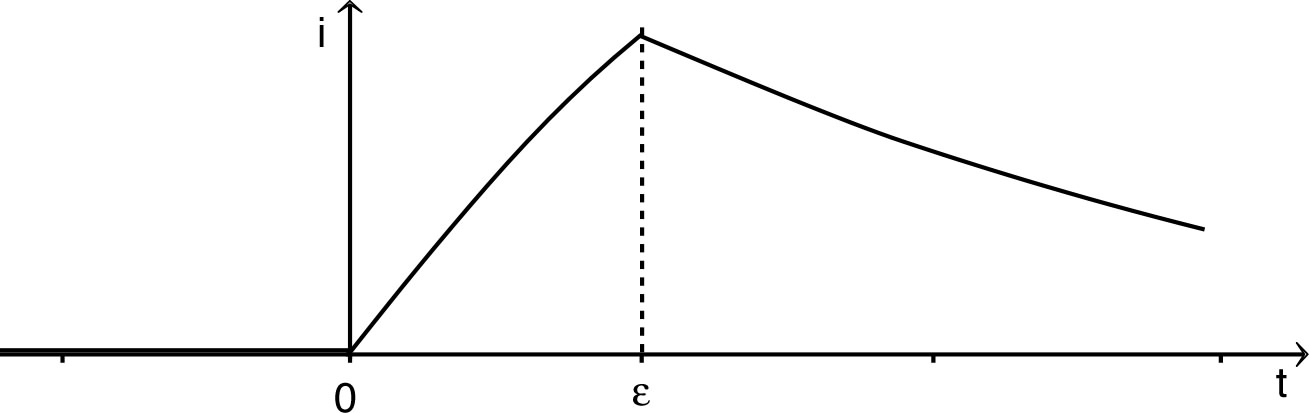 |
| 2.c. | • Pour
,
la limite
correspond à :
. • Pour , la limite correspond à : sur des durées d'un l'ordre de grandeur nettement inférieur à . • L'allure des variations du courant est la suivante. 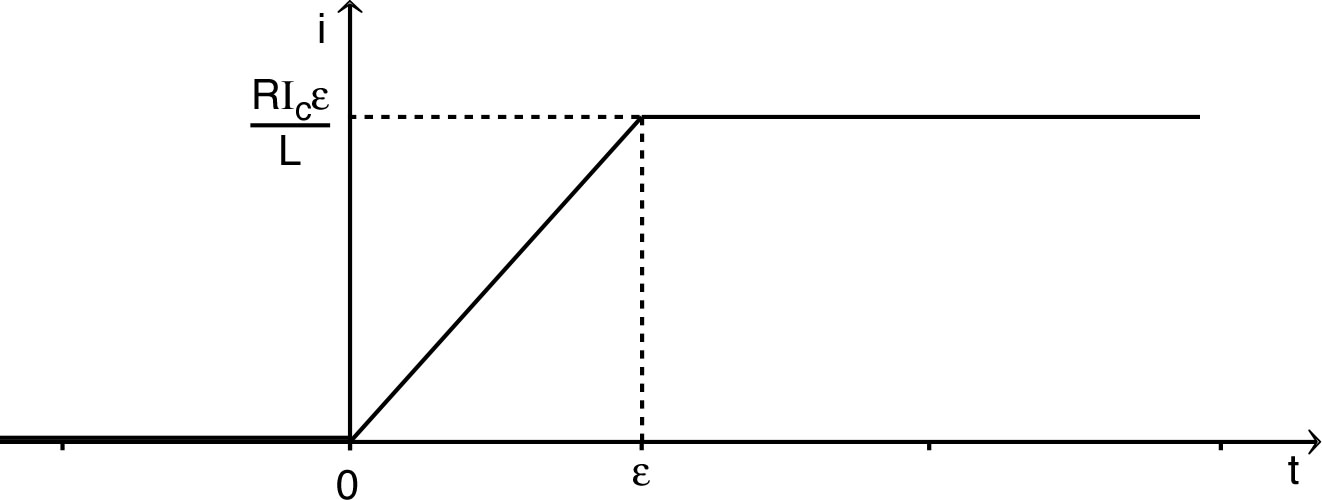 |
| 1. | • On peut considérer :
avec
et
; donc :
.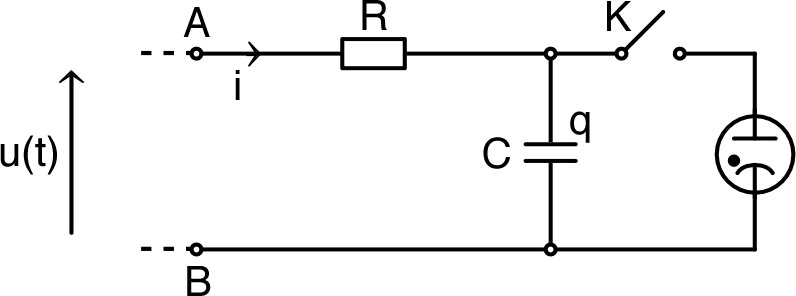 • Pour : et l’invariance du système conduit à . • Pour : et on obtient : où les conditions initiales donnent : ; par suite : et . |
| 2. | • Si l’interrupteur est fermé, le
comportement initial est le même tant que
(le tube à gaz se comporte alors comme un interrupteur
ouvert). • À l’instant où , le condensateur est “instantanément” déchargé, donc s’annule et le tube à gaz redevient “bloqué” ; ainsi la charge reprend comme initialement. • Ce phénomène se reproduit donc périodiquement, avec une fréquence . 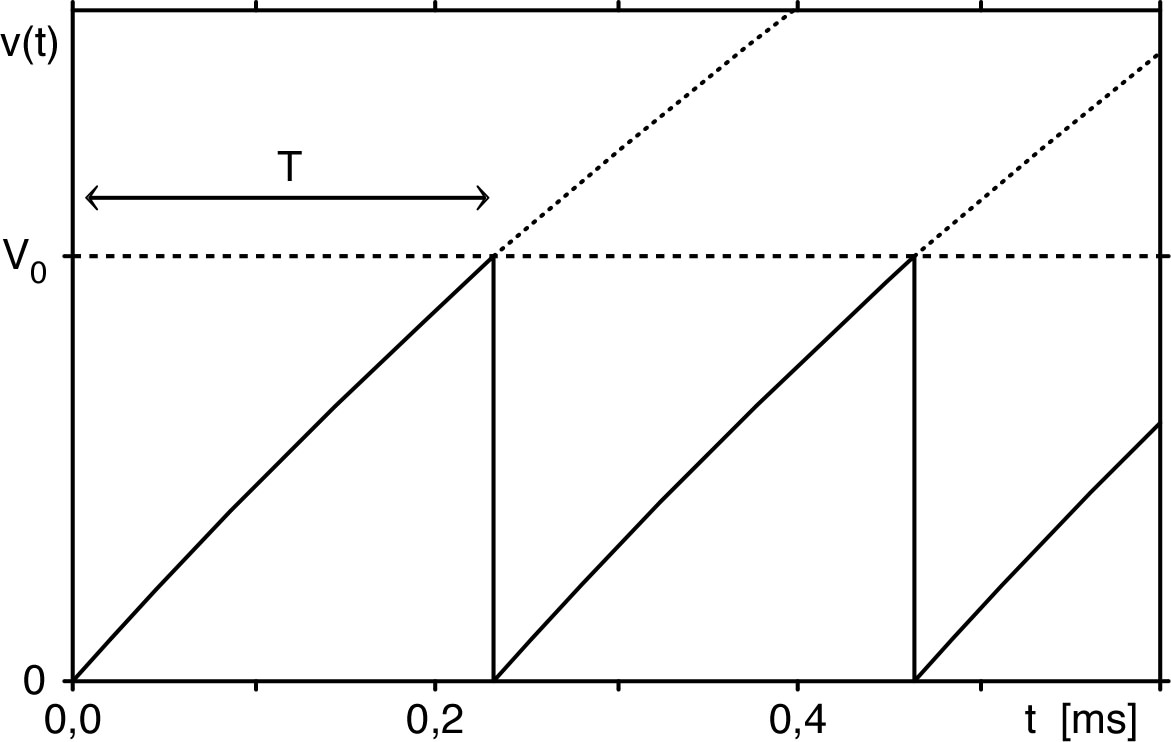 |
|
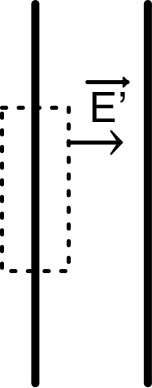 |
| 2.a. | • En opérant très lentement, la charge du
condensateur se rééquilibre en permanence pour
maintenir
,
donc il porte une charge :
(du côté + du générateur). Puisque
augmente,
diminue et
diminue, donc
. • Le générateur fournit donc : (en fait il absorbe de l'énergie au sens arithmétique). La résistance absorbe : qui est négligeable, car du second ordre, pour un mouvement très lent. Le condensateur absorbe : (en fait il fournit de l'énergie au sens arithmétique, comme le laisse prévoir le sens qu'il impose au courant). • Au total (il s'agit d'un travail mécanique positif car les charges de signes contraires portées par les deux plaques s'attirent), le travail à fournir au système est :
|
||
| 2.b. | • En opérant très rapidement, la charge du
condensateur ne peut pas se rééquilibrer “instantanément” à
cause de la résistance qui
limite le courant (constante de temps
).
En considérant la limite d'un mouvement “quasi-instantané”,
on peut supposer que la charge n'a pratiquement pas changé
pendant le mouvement ; le générateur et la résistance
n'absorbent donc rien pendant ce mouvement. • Le condensateur absorbe : ; le travail à fournir au système (sous forme mécanique) est : (il s'agit d'un travail mécanique positif car les charges de signes contraires portées par les deux plaques s'attirent). ◊ remarque : . |
| 3. | • Dans les deux cas, il finit par y avoir équilibre avec , donc il circule : . Le générateur fournit donc : (il absorbe de l'énergie au sens arithmétique). Dans le second cas, ce travail correspond aux effets du courant qui apparaît “juste après” le déplacement pour rétablir l'équilibre (arithmétiquement, le condensateur cède alors de l'énergie au générateur et à la résistance). |
| 4. | • La résistance absorbe :
qui est négligeable, car du second ordre, pour un mouvement
très lent. Plus précisément, on peut imposer
où
est une valeur d'autant plus petite que le mouvement est
lent ; par suite :
. Or
et
sont indépendants du mouvement, donc
peut être rendu arbitrairement petit en diminuant
, c'est-à-dire en ralentissant le mouvement. • Pour un mouvement très rapide, on peut considérer que puisque la charge du condensateur n'a pratiquement pas eu le temps de varier. Par la suite, la loi des mailles implique une évolution telle que : avec . • Les solutions sont de la forme : avec ; d'après les conditions initiales : . • On en déuit : et . ◊ remarque : . |
| 5. | • Pour le cas lent (réversible) :
(où est
l'énergie électrique dans le condensateur) ; ceci correspond
à dire que la variation de l'énergie du circuit (générateur
+ résistor + condensateur) est égale au travail mécanique
reçu par ce système. • Pour le cas très rapide (irréversible) : ; ceci correspond à dire que la variation d'énergie du système, y compris l'énergie thermique du résistor (il s'échauffe par l'effet Joule), est égale au travail mécanique reçu. ◊ remarque : on peut vérifier que . |