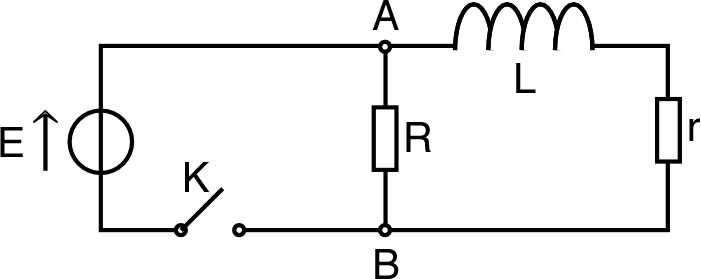
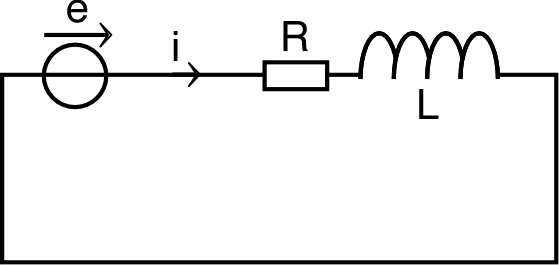
• À l'instant on ferme l'interrupteur ; déterminer les courants dans la résistance et dans la bobine d'inductance et de résistance .
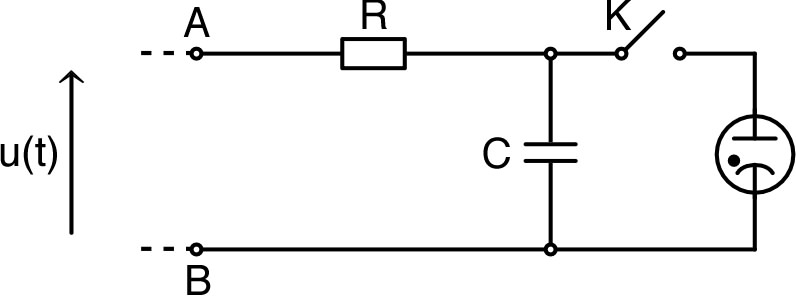
| 1. • On considère le
circuit ci-contre. • À l'instant on ferme l'interrupteur ; déterminer les courants dans la résistance et dans la bobine d'inductance et de résistance . |
 |
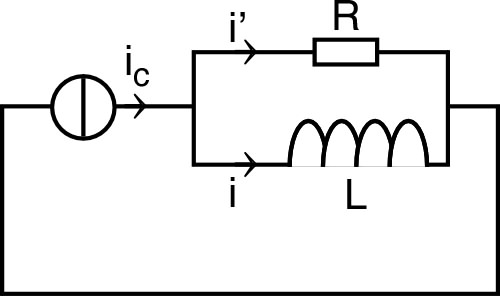
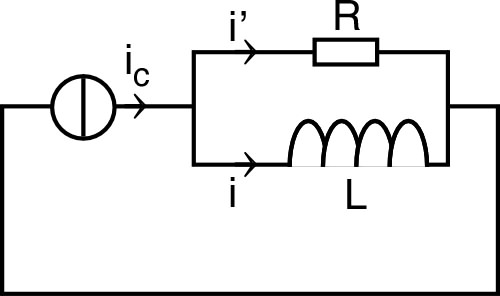
| 1. • On branche le
générateur en série avec un montage “RL” parallèle (la
résistance de la bobine est supposée négligeable :
inductance parfaite). a) Quelle est la relation entre , et ? b) Écrire l'équation différentielle régissant l'évolution de . Sans aucun calcul, indiquer quelle est “normalement” la valeur de pour ? |
 |
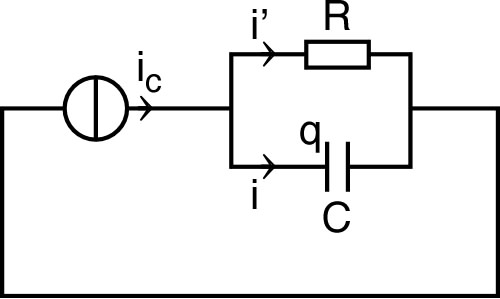
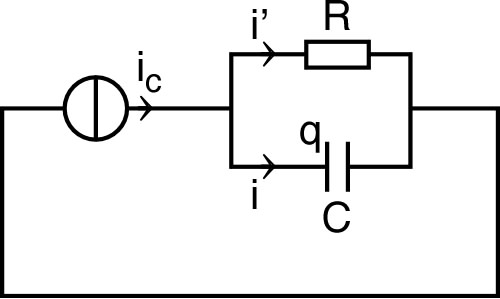
| 2. • On branche ce
générateur en série avec un montage “RC” parallèle. a) Quelle est la relation entre , et ? Quelle est la relation entre , , et ? Quelle est la relation entre et ? b) Écrire l'équation différentielle régissant l'évolution de . Sans aucun calcul, indiquer quelle est “normalement” la valeur de pour ? |
 |
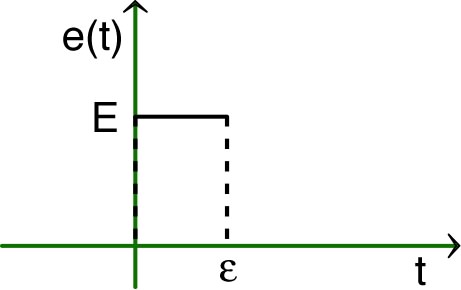
| •
Une “impulsion” de tension correspond au signal généré par
une source de tension parfaite de f.e.m. :
pour
; puis
(constant) pour
; puis
pour
. • La durée est très inférieure aux constantes de temps des circuits étudiés, mais nettement supérieure aux durées caractéristiques de l'ARQS. |
 |
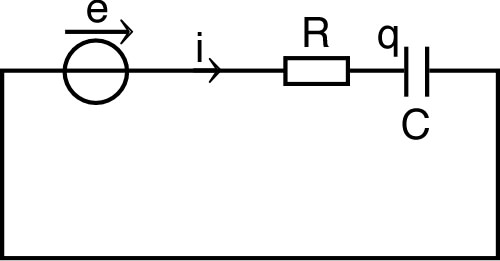
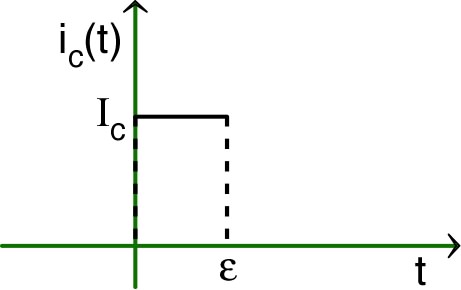
| •
Une “impulsion” de courant est le signal généré par une
source de courant parfaite dont le courant “de
court-circuit” est :
pour
; puis
(constant) pour
; puis
pour
. • La durée est très inférieure aux constantes de temps des circuits étudiés, mais nettement supérieure aux durées caractéristiques de l'ARQS. |
 |