EC.V - RÉGIMES TRANSITOIRES

EC.V - RÉGIMES TRANSITOIRES - CIRCUIT RLC

1. Équation générale

• Pour un circuit “RLC” en série, la loi des mailles peut s'écrire :

\displaystyle R \:i+L \: \frac{di}{dt}+\frac{1}{C} \,∫ \,i(t) \:dt=e(t)

Il est toutefois préférable de choisir la variable plus adaptée

\displaystyle u=\frac{q}{C}

; ainsi :

\displaystyle \frac{1}{ω_0^{\:2}} \, \ddot{u}+\frac{2\,α}{ω_0^{\:2}} \, \dot{u}+u=e(t)

avec

\displaystyle α=\frac{R}{2 \,L}

;

\displaystyle ω_0=\frac{1}{\sqrt{L \,C}}

◊ remarque : on peut aussi utiliser le “facteur de qualité”

\displaystyle 𝒬=\frac{ω_0}{2 \,α}

avec lequel l'équation s'écrit :

\displaystyle \frac{1}{ω_0^{\:2}} \, \ddot{u}+\frac{1}{𝒬\:ω_0} \, \dot{u}+u=e(t)

.

☞ remarque : des calculs analogues se retrouvent en mécanique :

\displaystyle L \:\ddot{q}+R \:\dot{q}+\frac{1}{C} \, q=E \: ↔ \: m \:\ddot{x}+λ \:\dot{x}+k \:x=F

;

x↔q

;

\displaystyle k↔\frac{1}{C}

;

\displaystyle T=k \:x↔u=\frac{1}{C} \, q

;

\displaystyle \frac{1}{2} k \:x^2↔\frac{1}{2\,C} \, q^2=\frac{1}{2} C \:u^2

;

v=\dot{x}↔i=\dot{q}

;

f=λ \:v↔u=R \:i

;

m↔L

;

\frac{1}{2} m \,v^2↔\frac{1}{2} L \:i^2

• Pour chercher les solutions d'une équation différentielle linéaire, on peut utiliser le fait que la différence de deux solutions est solution d'une équation simplifiée (dite “homogène”) dont le second membre est nul.

Ainsi, la solution générale de l'équation complète peut être calculée comme la somme :

◊ d'une solution particulière de l'équation complète ;
◊ de la solution générale de l'équation homogène.

Pour un circuit soumis à un échelon de tension :

e(t)=E

E'

est “constante par morceaux” ; on peut donc chercher une solution particulière constante par morceaux. On vérifie alors que

u(t)=e(t)

est solution (pour chaque morceau).

Pour l'équation homogène, on cherche des solutions de même forme que leurs dérivées (pour obtenir un total nul) ; on peut les chercher sous la forme

U_0 \: \mathrm{e}^{r \,t}

(avec des constantes

U_0

r∈ℂ

). On aboutit alors à l'équation caractéristique :

r^2+2 \,α \:r+ω_0^{\:2}=0

dont le discriminant est :

Δ=4 \:(α^2-ω_0^{\:2})

2. Régime pseudo-périodique

• Dans le cas

Δ<0

, c'est-à-dire

\displaystyle R<R_c=2 \:\sqrt{\frac{L}{C}}

, on obtient les racines :

r'=-α+j ω

r''=-α-j ω

avec

ω=\sqrt{ω_0^{\:2}-α^2}

(et

j^2=-1

• Pour

t≤0

, la solution (forcément réelle) est de la forme pseudo-périodique :

u(t)=\mathrm{e}^{-α \,t} \: [A \: \cos(ω \:t)+B \: \sin(ω \:t)]+E

, mais la seule solution physiquement acceptable est :

u(t)=E

constante.

Pour

t≥0

, la solution s'écrit :

u(t)=\mathrm{e}^{-α \,t} \: [A' \: \cos(ω \:t)+B' \: \sin(ω \:t)]+E'

; selon les conditions initiales (

u(0)=E

;

i(0)=C \:\dot{u}(0)=0

) on en déduit :

\displaystyle u(t)=(E-E') \: \mathrm{e}^{-α \,t} \: [\cos(ω \:t)+\frac{α}{ω} \, \sin(ω \:t)]+E'

.

☞ rappel : la capacité impose la continuité de

q=C \:u

; l'inductance impose la continuité de

i=C \:\dot{u}

◊ remarque : la quantité

\displaystyle T=\frac{2π}{ω}

(pseudo-période) correspond au “double écart” entre extremums relatifs, ou entre passages par la valeur limite

E'

, ou encore entre points de tangence avec “l'enveloppe” (légèrement décalés par rapport aux extremums).

◊ remarque : la tangente pour

t=0

est horizontale (le courant ne peut pas varier brusquement à cause de l'inductance) donc l'amplitude des enveloppes exponentielles pour

t=0

est :

\displaystyle (E'-E) \sqrt{1+\frac{α^2}{ω^2}}>(E'-E)

.

◊ remarque : le logarithme du rapport entre deux maximum (ou minimums, ou points de tangence supérieurs, ou points de tangence inférieurs) successifs est appelé “décrément logarithmique” :

δ=α \:T

.

• Le courant de charge du condensateur de capacité

C

est alors de la forme :

\displaystyle i(t)=C \:\frac{du}{dt}=\frac{E'-E}{L \:ω} \: \mathrm{e}^{-α \,t} \; \sin(ω \:t)

3. Régime apériodique

• Dans le cas

Δ>0

, c'est-à-dire

\displaystyle R>R_c=2 \:\sqrt{\frac{L}{C}}

, on peut écrire :

r'=-α+β

r''=-α-β

avec

β=\sqrt{α^2-ω_0^{\:2}}

• Pour

t≤0

, la solution peut s'écrire :

u(t)=A \:\mathrm{e}^{-λ \,t}+B \:\mathrm{e}^{-μ \,t}+E

(en posant :

λ=α-β>0

μ=α+β>λ

) mais la seule solution physiquement acceptable est :

u(t)=E

constante.

Pour

t≥0

, la solution est de la forme :

u(t)=A' \:\mathrm{e}^{-λ \,t}+B' \:\mathrm{e}^{-μ \,t}+E'

; d'après les conditions initiales :

\displaystyle u(t)=\frac{E-E'}{μ-λ} \:\left(μ \:\mathrm{e}^{-λ \,t}-λ \:\mathrm{e}^{-μ \,t}\right)+E'

◊ remarque :

◊	le terme $\mathrm{e}^{-μ \,t}$ décroît très vite et n'a d’influence que pour $t≈0$ (tangente horizontale pour $t=0$ car les variations du courant sont limitées par l'inductance) ;
◊	ensuite, le terme $\mathrm{e}^{-λ \,t}$ est prépondérant et son amplitude pour $t=0$ est : $(E'-E) \, \frac{μ}{μ-λ}>(E'-E)$ ;
◊	la représentation à plus grande échelle a l’allure ci-contre.

• Le courant de charge du condensateur est dans ce cas de la forme :

\displaystyle i(t)=C \, \frac{du}{dt}=\frac{E-E'}{2 \:L \:β} \, (\mathrm{e}^{-λ \,t}-\mathrm{e}^{-μ \,t} )

◊ remarque : ici encore le terme

\mathrm{e}^{-μ \,t}

décroît très rapidement.

4. Régime critique

◊ remarque : le cas critique est une limite mathématique pouvant sembler sans intérêt physique ; en pratique, son étude est très utile car nombreux sont les dispositifs pour lesquels un fonctionnement quasi-critique est très bénéfique.

• Pour

Δ=0

(

\displaystyle R=R_c=2 \;\sqrt{\frac{L}{C}}

) la valeur

r=-α=-ω_0

est racine double.

Or, la solution générale d'une équation différentielle du second ordre doit dépendre de deux constantes d'intégration, donc il doit y avoir d'autres solutions que celles de la forme

U_0 \: \mathrm{e}^{r \,t}

.

Les fonctions du type

P(t) \:\mathrm{e}^{r \,t}

avec

P(t)

polynôme sont aussi de même forme que leurs dérivées ; on obtient ainsi la solution générale “homogène” avec un polynôme du premier degré.

◊ remarque : on peut aussi retrouver ceci par la méthode de “variation de la constante” appliquée à

U_0

.

• Pour

t≤0

, la solution est de forme :

u(t)=(A+B \:t) \;\mathrm{e}^{-α \,t}+E

(apériodique “critique”) mais la seule solution physiquement acceptable est :

u(t)=E

constante.

Pour

t≥0

, la solution est de forme :

u(t)=(A'+B' \:t) \;\mathrm{e}^{-α \,t}+E'

et d'après les conditions initiales :

u(t)=(E-E')(1+α \:t)\;\mathrm{e}^{-α \,t}+E'

◊ remarque : le terme

1+α \:t

rend horizontale la tangente à

t=0

(le courant ne peut pas varier brusquement à cause de l'inductance).

• Le courant de charge du condensateur est alors de la forme :

\displaystyle i(t)=C\, \frac{du}{dt}=\frac{E-E'}{L\:} \: t \;\mathrm{e}^{-α \,t}

; maximum pour

\displaystyle t=\frac{1}{α}=\frac{1}{ω_0} =\frac{2 \,L}{R}=\frac{R \,C}{2}

📖 exercices n° I, II et III.

5. Temps de réponse à 5 %

• Le régime critique correspond environ à l'amortissement le plus rapide. Pour préciser, on peut estimer le “temps de réponse à

5 \:%

”

T_r

en fonction de

α

(ou en “variables réduites”

ω_0 \, T_r

en fonction de

\displaystyle ξ=\frac{α}{ω_0}

) :

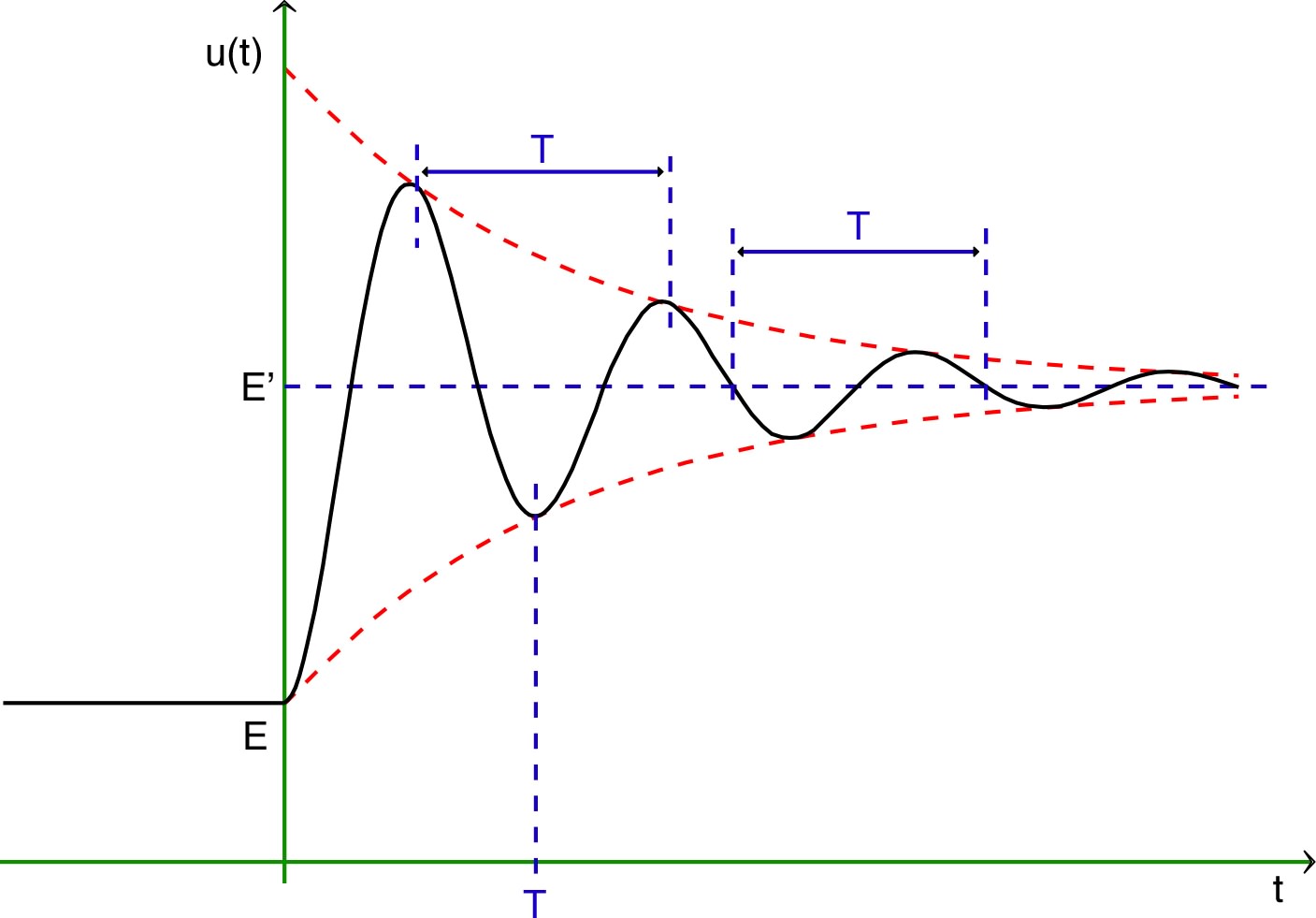
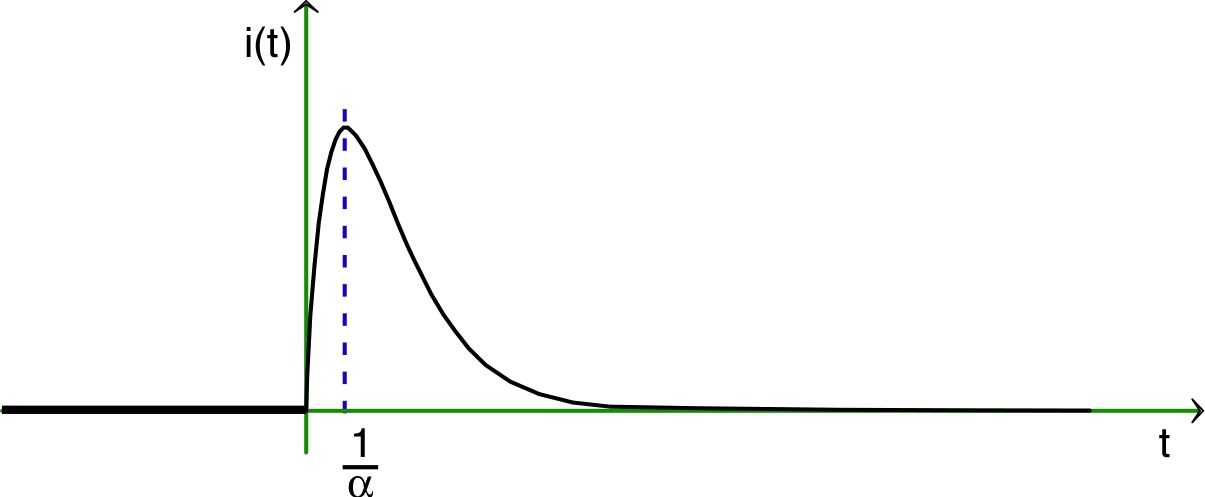
◊	pour le régime pseudo-périodique ( $ξ<1$ ) l'amortissement est décrit essentiellement par $\mathrm{e}^{-α \,t}$ ; ainsi $\displaystyle ω_0 \,T_r≈\frac{\ln(20)}{ξ}$ ;
◊	pour le régime apériodique ( $ξ>1$ ) l'amortissement est décrit essentiellement par $\mathrm{e}^{-λ \,t}$ ; ainsi $ω_0 \,T_r≈2 \,ξ \; \ln(20)$ ;
◊	pour le régime critique ( $ξ=1$ ) l'amortissement est décrit essentiellement par $α \:t \;\mathrm{e}^{-α \,t}$ ; ainsi $ω_0 \,T_r≈\text{4,74}$ (résolution numérique) ;
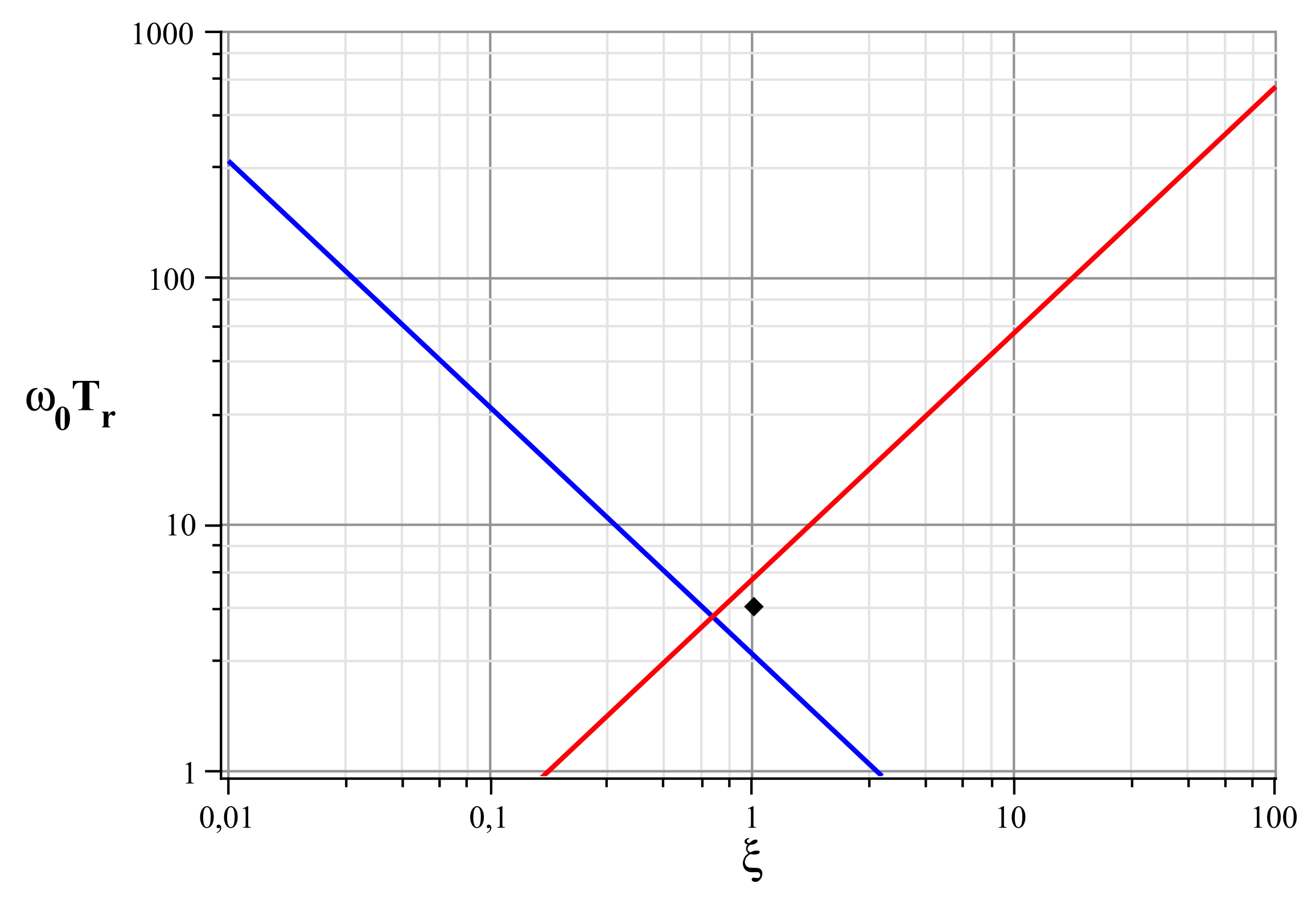
◊	l'intersection des deux comportements asymptotiques correspond à $ξ≈\text{0,}7$ et $ω_0\, T_r≈3$ .

6. Portrait de phase

• L'énergie emmagasinée dans l'inductance et le condensateur peut s'écrire :

\displaystyle ℰ=\frac{1}{2} L \:i^2+\frac{1}{2} C \:u^2=\frac{1}{2} C .\left(u^2+\left(\frac{\dot{u}}{ω_0} \right)^2 \right)

Dans un “espace des phases” avec les coordonnées

\displaystyle \left(u \:;\frac{\dot{u}}{ω_0} \right)

, les courbes d'énergie constante sont des cercles centrés à l'origine.

Lors d'une “décharge” (générateur éteint), compte tenu de la dissipation d'énergie par la résistance, les courbes parcourues sont plus ou moins des spirales rejoignant l'origine.