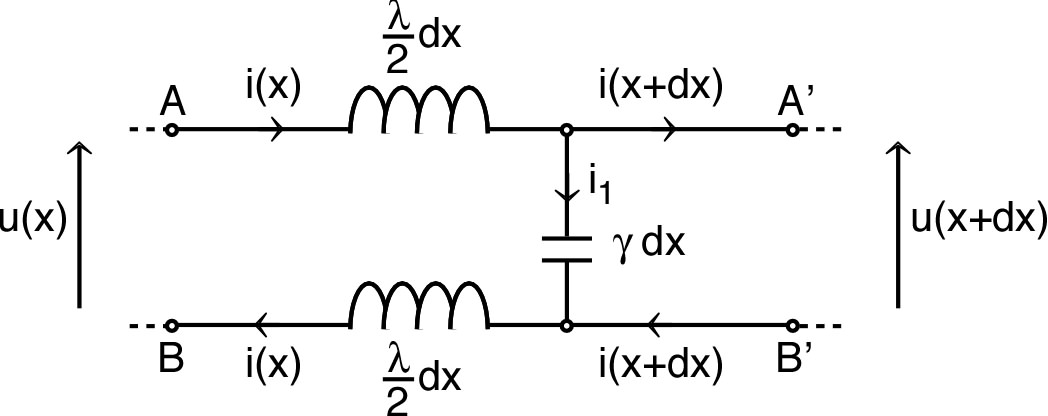
a) Quelle est la relation entre , , et ? Quelle est la relation entre , , et ?
b) Quelle est la relation entre , , et ? Quelle est la relation entre et ?
c) Écrire l'équation différentielle régissant l'évolution de .
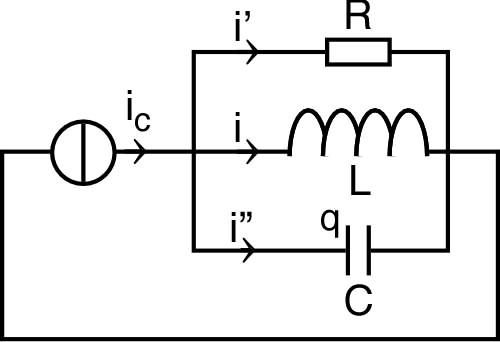
| 1. • On branche le
générateur en série avec un montage “RLC” parallèle (la
résistance de la bobine est supposée négligeable :
inductance parfaite). a) Quelle est la relation entre , , et ? Quelle est la relation entre , , et ? b) Quelle est la relation entre , , et ? Quelle est la relation entre et ? c) Écrire l'équation différentielle régissant l'évolution de . |
 |
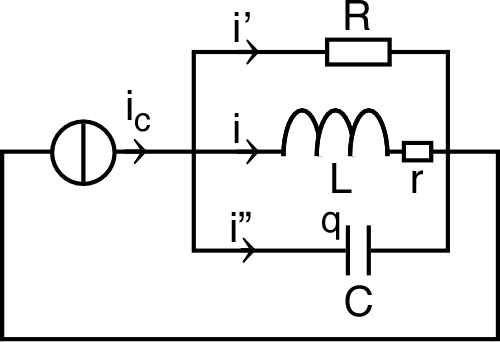
| 4. • On souhaite
maintenant tenir compte de la résistance de la
bobine, conformément au schéma ci-contre. a) Établir l'équation sur remplaçant celle de la question (1). b) Montrer que, dans des conditions à préciser, il peut exister des valeurs , , et utilisées dans le montage (1) afin de redonner la même équation que celle de la question (4). c) En supposant qu'on choisisse , établir les expressions de et en fonction de , , et . |
 |
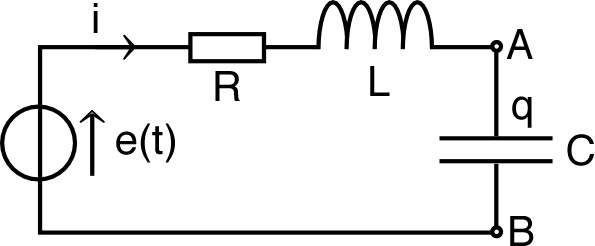
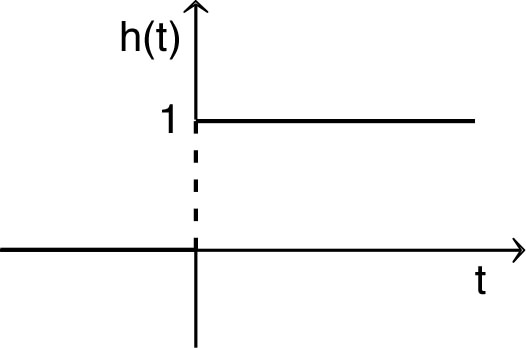
| • On
considère un générateur de tension parfait, de force
électromotrice :
pour
puis
pour
(échelon de tension). • Ce générateur étant branché dans un montage “RLC” série ; on étudie l'évolution de la tension aux bornes du condensateur pour . On note et . |
 |
 |
 |
| 1. a) Montrer que
: . b) Montrer que : . c) On nomme “fonction de Heaviside” la fonction échelon unité. Montrer que : et que : . d) Calculer pour . |
 |
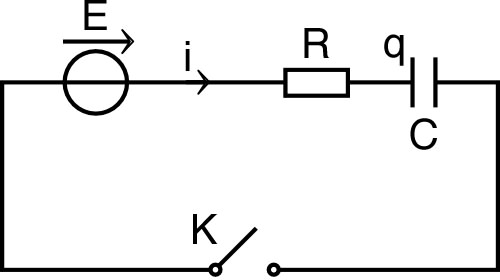
| 2. • On considère
maintenant le circuit ci-contre, dans lequel le condensateur
est initialement déchargé. a) À on ferme l'interrupteur. Montrer que l'ensemble du générateur et de l'interrupteur équivaut à un générateur de f.e.m. . b) Écrire l'équation intégro-différentielle donnant le courant en fonction de . c) En posant : et , trouver la relation entre et . En déduire puis en déduire . |
 |
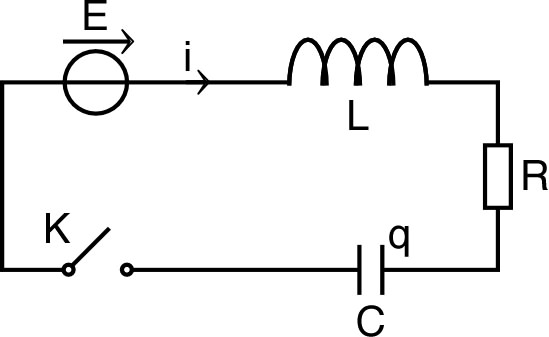
| 3. • On considère
maintenant le circuit ci-contre, dans lequel le condensateur
est initialement déchargé. a) Écrire l'équation intégro-différentielle entre et . b) En posant : et , trouver la relation entre et . c) Décomposer en éléments simples en supposant que le polynôme : admette deux racines distinctes et , réelles ou imaginaires (on omet le régime d'amortissement critique). |
 |