E.M.VI - THÉORÈME D’AMPÈRE

Flux magnétique (conservatif)

• Contrairement à l’électrostatique, il n’y a pas de “charges magnétiques” et, pour une surface

S

fermée, le flux magnétique est nul :

\displaystyle Φ=\oiint_S \,\overset{→}{B}⋅d\overset{→}{S}=0

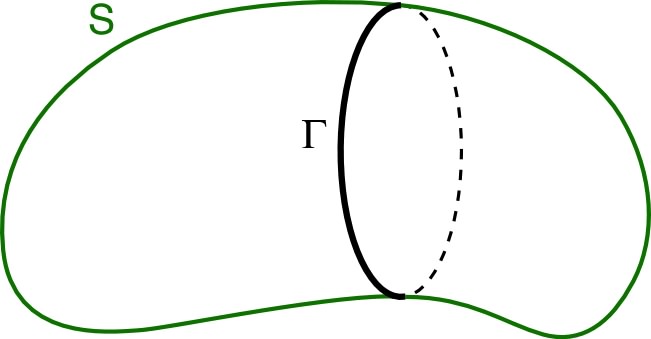
De ce fait, pour un contour fermé

Γ

, le flux est le même à travers toute surface de bord

Γ

(en orientant la surface selon l’orientation du contour) ; on cite généralement cette propriété en disant que le flux magnétique est “conservatif”.

• Ceci peut se démontrer dans le cas du champ d’un fil rectiligne “infini”, pour lequel les lignes de champ sont des cercles ayant le fil pour axe.

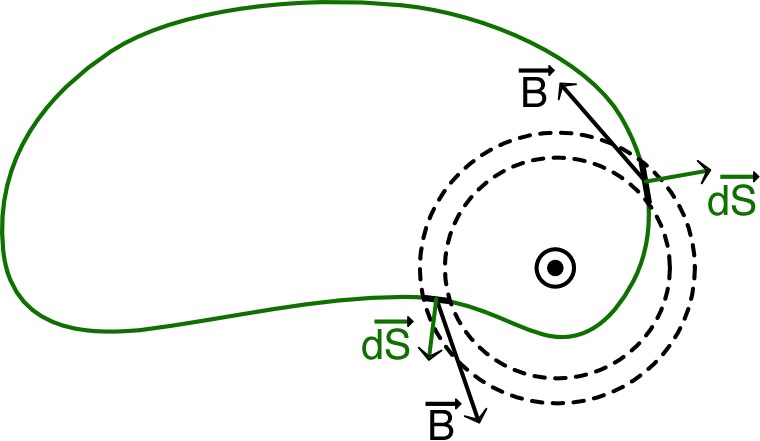
Le flux à travers toute surface fermée peut être décomposé en contributions infinitésimales à travers des “tubes de champ” toriques élémentaires.

Or les contributions algébriques

\overset{→}{B}⋅d\overset{→}{S}=±B_θ \: dS_θ

se compensent aux extrémités de tels tores.

Dans le cas général, la contribution

d\overset{→}{B}

de la loi de Biot et Savart possède les mêmes propriétés de symétrie, par rapport à l’élément de courant

\overset{→}{dℓ}

, que le champ

\overset{→}{B}

d’un fil rectiligne infini ; par suite

d\overset{→}{B}

a un flux conservatif et

\overset{→}{B}

aussi après intégration (compte tenu de l’additivité des flux).

◊ remarque : l'unité de base du flux magnétique est le

\mathrm{weber}

(symbole

\mathrm{Wb}

Théorème d’Ampère

• Contrairement au cas de l’électrostatique, la “circulation” du champ

\overset{→}{B}

sur un trajet fermé n’est pas forcément nulle, car la circulation

\displaystyle C=∫_M^N \overset{→}{B}⋅\overset{→}{d𝓁}

sur un trajet

MN

dépend en général du chemin suivi pour aller de

M

N

. De ce fait, le champ magnétique ne dérive pas d’un potentiel (scalaire).

◊ remarque : par contre, le champ magnétostatique dérive d’un “potentiel vecteur”, relation faisant intervenir l’opérateur “rotationnel” (non étudié ici).

• Pour un fil rectiligne “infini”, dont le champ peut s’écrire en coordonnées cylindriques

\displaystyle \overset{→}{B}=\frac{μ_0 \: I}{2π \:r} \: \overset{→}{u}_θ

, l’intégration le long d'une ligne de champ donne :

\displaystyle C=\frac{μ_0 \: I}{2π} \, ∫ dθ=μ_0 \: N \:I

où

N

est le nombre de tours du contour autour du fil.

Cette propriété se généralise à un champ magnétostatique quelconque ; elle peut s’écrire (théorème d’Ampère) :

\displaystyle C=∮_{\,Γ} \overset{→}{B}⋅\overset{→}{d𝓁}=μ_0 \: I_{int}

où

I_{int}

désigne le courant total “traversant” le contour fermé (compté un nombre de fois correspondant au nombre de tours).

Application au Solénoïde “infini”

• Pour un solénoïde rectiligne “infini” :

◊	la symétrie selon le plan perpendiculaire à l’axe et contenant le point $M$ étudié impose que $\overset{→}{B}$ est axial : $\overset{→}{B}(M)=\overset{→}{B}(r,θ,z)=B_z (r,θ,z) \: \overset{→}{u}_z$ ;
◊	les invariances par translation selon l’axe et par rotation autour de l’axe imposent : $B_z (r,θ,z)=B_z (r)$ ;
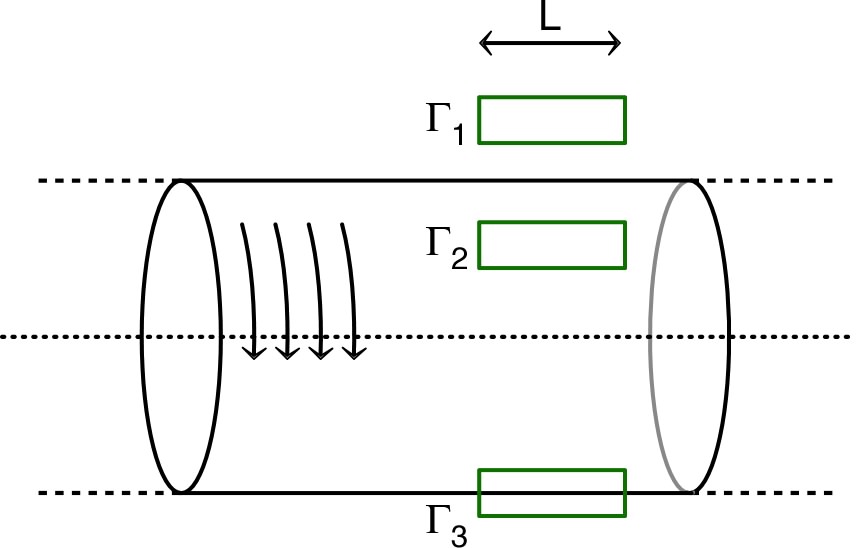
◊	la circulation sur les contours $Γ_1$ et $Γ_2$ est nulle, donc le champ est uniforme à l’intérieur et uniforme à l’extérieur (mais avec des valeurs respectives $B$ et $B'$ a priori différentes) ;
◊	la loi de Biot et Savart montre que le champ sur l’axe est $B=μ_0 \: n \:I$ où $n$ est le nombre de spires par unité de longueur, donc cette valeur correspond au champ uniforme à l’intérieur ;
◊	la circulation sur $Γ_3$ est : $C=(B-B') \:L=μ_0 \: N_L \: I$ , où $N_L$ est le nombre de spires pour la longueur $L$ , donc : $B-B'=μ_0 \: n \:I$ et $B'=0$ à l’extérieur.

◊ remarque : la loi de Biot et Savart est utile car on ne peut pas envisager la circulation sur une ligne de champ, infinie et non fermée (sinon il faut comparer avec les lignes de champ d'un solénoïde très long mais fini).

◊ remarque : on néglige ici l’aspect hélicoïdal des spires, dans la mesure où l’enroulement est assez “serré”.

📖 exercice n° I.