THÉORÈME D’AMPÈRE - corrigé des exercices

A. EXERCICE DE BASE

Solénoïde torique

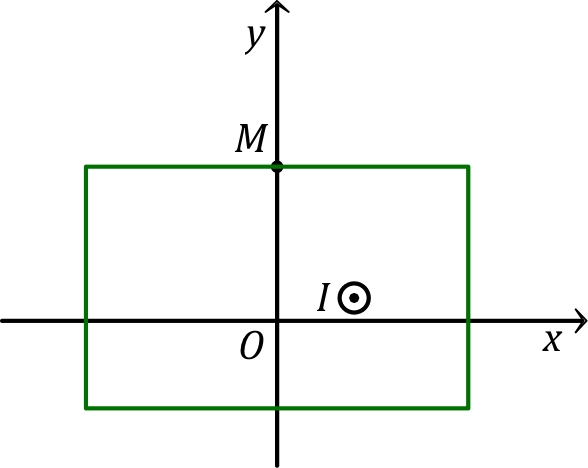
• Le solénoïde et le point

M

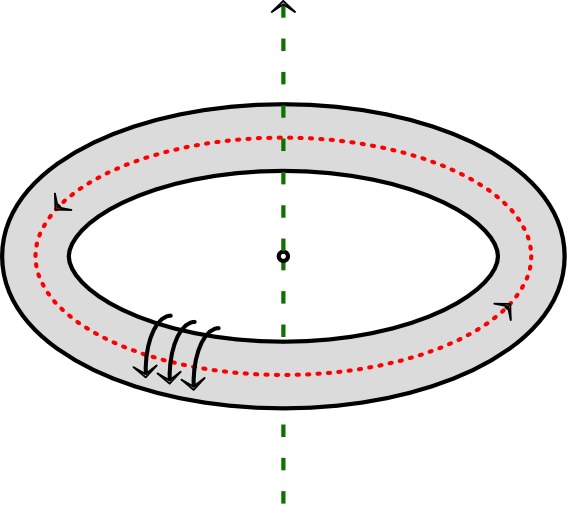
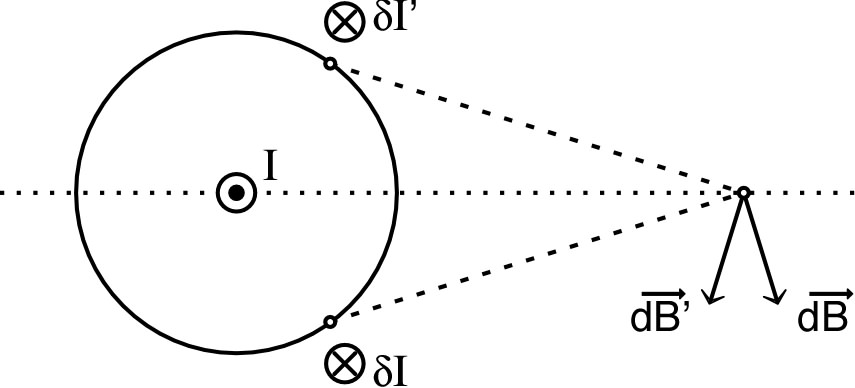
sont invariants dans une symétrie par rapport au plan contenant l’axe et

M

, donc

\overset{→}{B}

(pseudovecteur) est identique à l’opposé de son symétrique géométrique.
• Le symétrique géométrique doit donc être égal à l’opposé de

\overset{→}{B}

, ce qui impose au champ

\overset{→}{B}

d’être perpendiculaire au plan, c’est-à-dire :

\overset{→}{B}(r,θ,z) = B_θ (r,z) \:\overset{→}{u}_θ

(en coordonnées cylindriques).

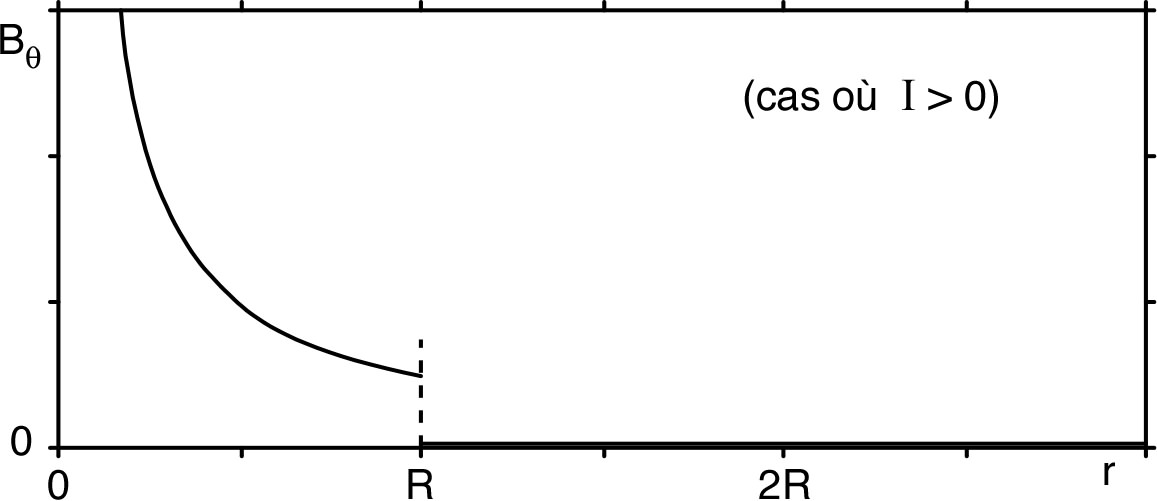
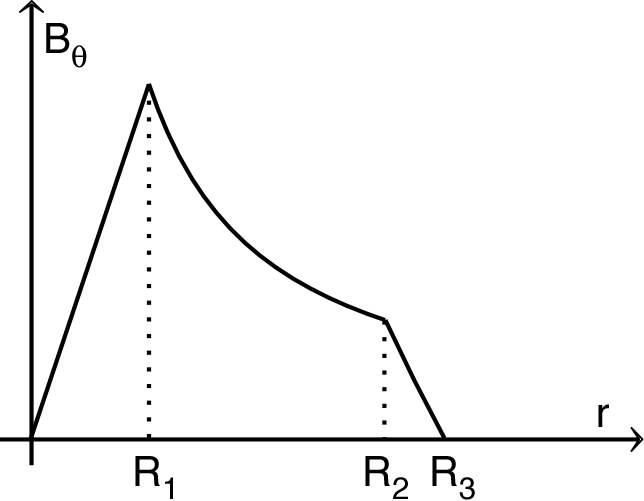
• La circulation sur une ligne de champ intérieure (circulaire) est :

C=2π \:r \:B_θ=μ_0 \: N \:I

où

N

est le nombre de spires, par conséquent :

\displaystyle B_θ (r)=\frac{μ_0 \: N \:I}{2π \:r}

(indépendant de

z

).
• La circulation sur une ligne de champ extérieure (circulaire) est :

C=2π \:r \:B_θ=0

, donc :

B_θ (r)=0

B. EXERCICES D’APPROFONDISSEMENT

Câble coaxial rectiligne “infini”

• Par symétrie on suppose que le courant dans le conducteur tubulaire est “réparti” uniformément sur la périphérie ; il correspond à un mouvement des charges parallèle à l’axe.

• Par symétrie, le champ est orthoradial :

\overset{→}{B}(r,θ,z)=B_θ (r,θ,z) \:\overset{→}{u}_θ

; en outre

B_θ

ne dépend que de

r

B_θ (r,θ,z)=B_θ (r)

.
• La circulation le long d’une ligne de champ coaxiale est :

C(r)=2π \:r \:B_θ (r)

;

◊ pour $r<R$ : $I_{int} (r)=I$ et $\displaystyle B_θ (r)=\frac{μ_0 \: I}{2π \:r}$ ;
◊ pour $r>R$ : $I_{int} (r)=0$ et $B_θ (r)=0$ .

◊ remarque : on obtient un champ qui tend vers l’infini quand on se rapproche du fil, mais en réalité ce dernier a forcément un diamètre non nul ; la discontinuité au bord externe vient du fait qu'on a négligé l'épaisseur.
◊ remarque : cet exemple, qui constitue une première approche vers l’utilisation d’une répartition de courant, montre un intérêt du câble coaxial vis-à-vis de la limitation des effets parasites.

Distribution volumique de courant

• Le dispositif est invariant par symétrie selon le plan contenant l'axe et le point

M

où on calcule le champ, ce dernier (pseudovecteur) doit donc être invariant par antisymétrie :

$B_r \: \overset{→}{u}_r+B_θ \: \overset{→}{u}_θ+B_z \: \overset{→}{u}_z=-\left[B_r \: \overset{→}{u}_r+ B_θ.(-\overset{→}{u}_θ) +B_z \: \overset{→}{u}_z \right]=-B_r \: \overset{→}{u}_r+B_θ \: \overset{→}{u}_θ-B_z \: \overset{→}{u}_z$ .

• On en déduit que le champ est orthoradial :

B_r=B_z=0

\overset{→}{B}=B_θ \: \overset{→}{u}_θ

• Les lignes de champ sont des cercles coaxiaux ; l'invariance du câble par translation et rotation selon l'axe impose que la coordonnée ne dépend que de

r

B_θ (r,θ,z)=B_θ (r)

.
• La circulation d'un champ sur un tel cercle est :

C(r)=2π \:r \:B_θ (r)

;

◊	pour $r<R_1$ : $\displaystyle I_{int} (r)=I \, \frac{π \:r^2}{π \:R_1^{\:2}}$ (le courant “intérieur” est proportionnel à la section “enlacée” par le contour) et $\displaystyle B_θ (r)=\frac{μ_0 \: I}{2π} \, \frac{r}{R_1^{\:2}}$ ;
◊	pour $R_1<r<R_2$ : $I_{int} (r)=I$ et $\displaystyle B_θ (r)=\frac{μ_0 \: I}{2π \:r}$ ;
◊	pour $R_2<r<R_3$ : $\displaystyle I_{int} (r)=I.\left(1-\frac{π \:r^2- π \:R_2^{\:2}}{π \:R_3^{\:2}- π \:R_2^{\:2}}\right)$ et $\displaystyle B_θ (r)=\frac{μ_0 \: I}{2π \:r} \, \frac{R_3^{\:2}-r^2}{R_3^{\:2}- R_2^{\:2}}$ ;
◊	pour $r>R_3$ : $I_{int} (r)=0$ et $B_θ (r)=0$ .

• Les expressions précédentes montrent que le champ est continu à la surface des conducteurs.

• Les variations de

B(r)=B_θ (r)

sont représentées ci-contre.

◊ remarque : cet exemple montre un intérêt du câble coaxial vis-à-vis de la limitation des effets parasites.

Champ magnétique et champ électrostatique

• Vu l'invariance par translation selon

xOz

, on peut raisonner pour

M

sur

Oy

.
• Le plan

xOy

est alors plan d'antisymétrie électrique (retournement du courant), donc de “symétrie magnétique” : le vecteur qui représente

\overset{→}{B}

lui est parallèle (géométriquement symétrique).
• Le plan

yOz

est alors plan de symétrie électrique, donc “d'antisymétrie magnétique” : le vecteur qui représente

\overset{→}{B}

lui est perpendiculaire (géométriquement antisymétrique) donc parallèle à

Ox

. Cette seconde condition est plus forte et englobe la précédente.
◊ remarque : on peut aussi s'inspirer de la symétrie de la loi de Biot et Savart, mais cette dernière s'applique a priori à un circuit (fermé) ; rien ne dit que cela ne fausse pas l'étude du cas étudié ici (tout modèle “infini” peut poser des problèmes de calculs de limites).

• On peut considérer un contour rectangulaire parallèle à

Ox

(côté de longueur

L

) et

Oy

.
• L'invariance du plan étudié par translation selon

Ox

Oz

montre que

B_x

ne dépend que de

y

.
• Pour

\overset{→}{B}=B_x (y) \: \overset{→}{u}_x

la circulation peut s'écrire :

$C=L .\left[B_x (y_{-})-B_x (y_{+})\right]=μ_0 \: J \:L$ .

• La relation précédente montre que

B_x (y)

est constant pour tout

y_{-}<0

et aussi pour tout

y_{+}>0

.
• On peut alors utiliser la symétrie selon

xOz

en choisissant

M'

symétrique de

M

y_M=y_{+}=-y_{-}=-y_{M'}

. Dans cette symétrie électrique, le champ

\overset{→}{B}

est antisymétrique :

\overset{→}{B}(M')=-\overset{→}{B}(M)

.
• Finalement :

C=-2 \,L \:B_x (y_M)=μ_0 \: J \:L

;

\displaystyle B_x (y_M)=-\frac{μ_0 \: J}{2}

3.a.	• Dans une bande $dx$ , la quantité de charge qui passe $z=Cste$ dans une durée $dt$ correspond à : $dI \:dt=J \:dx \:dt=σ \:dx \:dz$ avec $dz=v \:dt$ ; ainsi : $J=σ \:v$ .

3.b.	• Dans le modèle du plan “infini”, le champ électrique est (selon le théorème de Gauss) : $\displaystyle \overset{→}{E}(M)=\frac{σ}{2 \,ε_0} \: \overset{→}{u}_y=\frac{μ_0 \: c^2 \: J}{2 \,v} \: \overset{→}{u}_y$ (avec une symétrie selon $xOz$ ). • Cela correspond à : $\displaystyle \overset{→}{B}=\frac{\overset{→}{v} × \overset{→}{E}}{c^2}$ , ce qui suggère un lien avec un changement de référentiel relativiste. • Il importe toutefois ici de comprendre que, dans le référentiel fixe, le champ électrique (total) est nul par compensation, car le plan conducteur contient autant de charges immobiles de signe contraire. Si on raisonne dans le référentiel des charges en translation, le courant est le même (charges opposées avec vitesse opposée), donc on prédit le même champ électrique total nul et le même champ $\overset{→}{B}$ . • Si au contraire on applique la transformation électromagnétique suggérée par la transformation galiléenne de la force de Lorentz, on prédit un champ magnétique inchangé mais un champ électrique modifié de $\overset{→}{v} × \overset{→}{B}$ ; les deux ne sont pas cohérents. Cela peut provenir du raisonnement galiléen non relativiste pour la force, mais éventuellement aussi de la modélisation approximative par un plan infini (il faudrait tester si l'incohérence subsiste avec un calcul relativiste).

Champ magnétique d’une sphère chargée en rotation

• Les charges et courants sont invariants par symétrie selon le plan équatorial, donc pour tout point

M

de ce plan le champ

\overset{→}{B}(M)

y est orthogonal (antisymétrique car pseudovecteur), c'est à dire selon

Oz

.
• Les courants sont antisymétriques par rapport à tout plan contenant

Oz

, donc

\overset{→}{B}

y est parallèle à ces plans (

B_φ=0

) et sur l'axe il est parallèle à leur intersection (selon

Oz

).
• Si on fait l'hypothèse que le champ magnétique décroît suffisamment en s'éloignant de la sphère pour qu'on puisse intégrer la circulation sur un contour constitué de

{Ox}_{+}

{Oz}_{+}

et refermé par un quart de cercle centré en

O

et qu'on fait tendre vers l'infini, alors on peut dire que la circulation sur

{Ox}_{+}

est liée au courant généré par l'hémisphère nord. Hélas les symétries ne permettent pas d'en savoir plus (mais cela a au moins l'intérêt de montrer les limites de la méthode).

• Bien que cela soit moins l'esprit de l'exercice, on peut alors décrire les courants comme une somme de spires coaxiales selon

Oz

et raisonner avec la loi de Biot et Savart.
• La densité de charge est

\displaystyle σ=\frac{Q}{4π \:R^2}

.
• Une bande

R \:dθ

centrée en

z=R \: \cos(θ)

a un rayon

r=R \: \sin(θ)

; elle contient des charges qui se déplacent à la vitesse

v=r \:ω

. Cela correspond à une “densité de courant”

\displaystyle J=\frac{dI}{R \:dθ}=σ \:v

.
• Une telle bande crée en

O

un champ magnétique (axial) :

$\displaystyle dB_z=\frac{μ_0 \: dI \:r^2}{2 \,\left(r^2+z^2\right)^{3/2}}=\frac{μ_0 \: dI \:r^2}{2 \,R^3}=\frac{μ_0 \: σ \:v \:r^2}{2 \,R^2} dθ=\frac{μ_0 \: Q \:ω}{8π \:R} \; \sin^3(θ) \: dθ$ .

• Avec

∫_0^π \:\sin^3(θ) \: dθ=∫_{-1}^1 \:(1-u^2 ) \: du=\frac{4}{3}

on obtient finalement :

\displaystyle B_z (O)=\frac{μ_0 \: Q \:ω}{6π \:R}

• D'après le théorème de Gauss, le champ électrique (nul à l'intérieur) est radial à l'extérieur, avec au voisinage immédiat de la surface

\displaystyle E_r≈\frac{Q}{4π \:ε_0 \: R^2}=B_z (O) \: \frac{3 \,c^2}{2 \,R \:ω}

, ce qui peut évoquer un lien avec un changement de référentiel relativiste associé à la rotation.

• La notion de moment dipolaire correspond à une approximation à grande distance ; on peut donc en première approximation négliger la différence de position des différentes tranches de sphère considérées précédemment. Les différentes contributions sont selon

Oz

donc on ajoute algébriquement.
• Une tranche a pour moment dipolaire :

\displaystyle d𝓂=π \:r^2 \: dI=π \:r^2 \: σ \:v \:R \:dθ=\frac{Q \:R^2 \: ω}{4} \: \sin^3(θ) \: dθ

; ainsi au total :

\displaystyle 𝓂≈\frac{Q \:R^2 \: ω}{3}