THÉORÈME D’AMPÈRE - exercices

A. EXERCICE DE BASE

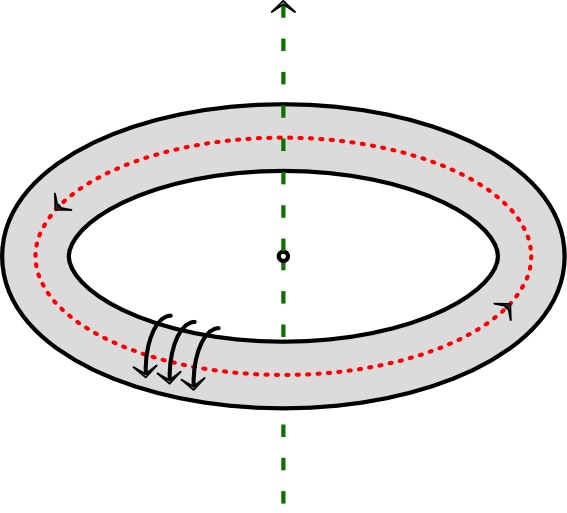
Solénoïde torique

• On considère un solénoïde torique d’axe $Oz$ , de grand rayon $R$ et de petit rayon $ρ$ ,  comportant $N$ tours de fil, est parcouru par un courant $I$ . ◊ remarque : pour simplifier, le schéma ci-contre ne représente que quelques unes des spires enroulées sur le tore ; il représente en outre une ligne de champ intérieure au tore. • D’après les symétries, déterminer la direction du champ $\overset{→}{B}$ en un point $M$ quelconque de l’espace. • Calculer le champ magnétique $\overset{→}{B}$ en un point $M$ quelconque.

B. EXERCICES D’APPROFONDISSEMENT

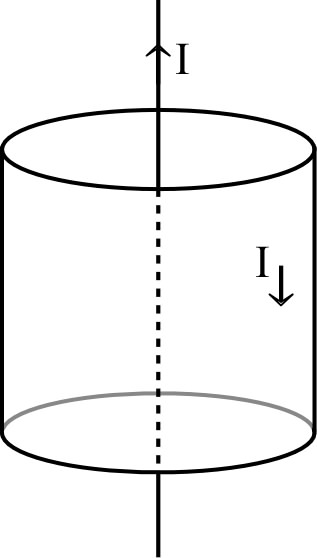
Câble coaxial rectiligne “infini”

• On considère un câble coaxial, constitué d’un fil rectiligne “infini” associé à un conducteur tubulaire coaxial, de rayon $R$ , par lequel s’effectue le “retour” du courant. ◊ remarque : on considère que le courant de “retour” se répartit de façon uniforme sur le pourtour du conducteur tubulaire. • Calculer le champ magnétique créé par ce câble en chaque point de l’espace (intérieur et extérieur).

Distribution volumique de courant

• Un câble coaxial est constitué par un conducteur cylindrique plein, de rayon $R_1$ , entouré par un conducteur externe occupant le volume compris entre les rayons $R_2$ et $R_3$ (avec  $R_3>R_2>R_1$ )  ;  les trois cylindres ainsi considérés étant coaxiaux.

• Un courant $I$ circule dans le conducteur intérieur et “revient” dans l’autre sens dans le conducteur extérieur. On suppose que le courant est uniformément réparti dans la section des conducteurs (c’est-à-dire proportionnellement à l’aire de la section considérée).

• D’après les symétries, déterminer la direction du champ $\overset{→}{B}$ en un point $M$ quelconque de l’espace.

• Calculer le champ magnétique $\overset{→}{B}$ en un point $M$ quelconque, en fonction de la distance $r$ de l’axe.

• Tracer la courbe représentative de $B(r)$ . Le champ est-il continu à la surface des conducteurs ?

Champ magnétique et champ électrostatique

• L’espace étant rapporté à un trièdre cartésien orthonormé, le plan $xOz$ est parcouru par un courant “superficiel” uniforme parallèle à $Oz$ ; c’est-à-dire que chaque bande de largeur $dx$ , dont les côtés sont parallèles à $Oz$ , est parcourue par un courant :  $dI=J \:dx$  (où $J$ est une constante).

• En utilisant la symétrie du problème, déterminer la direction du champ magnétique $\overset{→}{B}(M)$ en un point $M$ situé au voisinage de $xOz$ (ce qui revient à considérer le courant dans un plan “infini”).

• Appliquer le théorème d’Ampère à un circuit judicieusement choisi, puis en déduire le champ magnétique en “tout” point de l’espace extérieur au plan $xOz$ .

a) Montrer que ce courant superficiel peut être considéré comme une répartition superficielle de charge $σ$ en mouvement de translation à une vitesse $v$ . Exprimer $J$ en fonction de $σ$ et $v$ .

b) Quelle est la relation entre le champ magnétique calculé dans ce problème et le champ électrostatique $\overset{→}{E}$ créé par un plan uniformément chargé d’une densité surfacique $σ$ ?

Champ magnétique d’une sphère chargée en rotation

• Une sphère de rayon $R$ porte une charge totale $Q$ répartie uniformément sur sa surface. Cette sphère est animée d’un mouvement de rotation à la vitesse angulaire $ω$ autour d’un de ses diamètres (par exemple l’axe $Oz$ , en notant $O$ le centre de la sphère) ; on suppose que les charges sont entraînées, sans modification de leur répartition, par le mouvement de la sphère.

• Calculer le champ magnétique $\overset{→}{B}$ ainsi créé au centre de la sphère.

• Exprimer ce champ magnétique en fonction du champ électrostatique $\overset{→}{E}$ créé au voisinage immédiat à l’extérieur de la sphère.

• Calculer le moment magnétique $\overset{→}{𝓂}$ de cette distribution de courant.