 |
 |
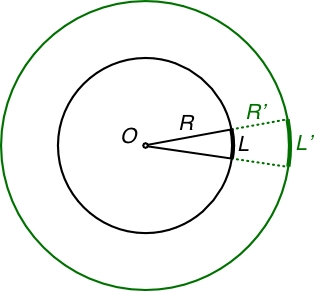
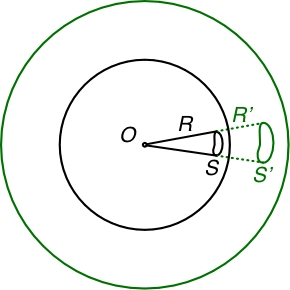
| Pour une charge ponctuelle : où est l’angle solide sous lequel on “voit” à partir de la position de . |
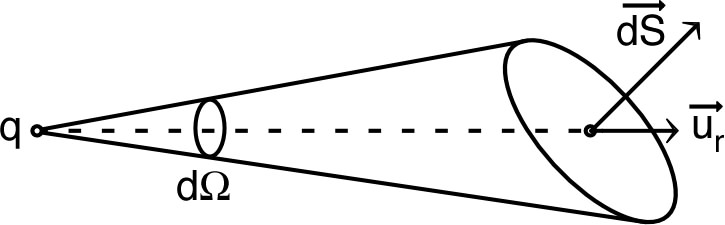
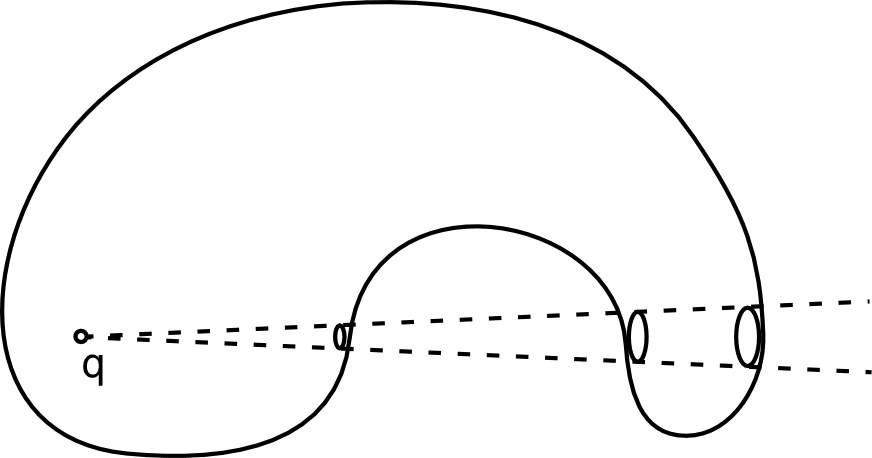
| Ainsi, pour une surface S fermée, le flux sortant se déduit par addition des charges intérieures : (théorème de Gauss). |
• Pour une boule de rayon ,
chargée d’une densité volumique
uniforme (donc de charge totale
) :
|
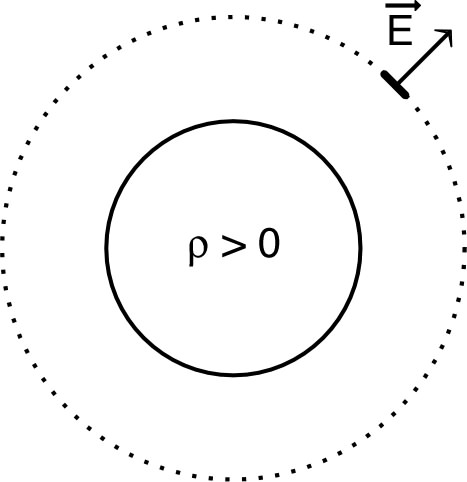 |
◊ pour :
|
 |
| ☞ remarque : pour une distribution à symétrie sphérique, le champ extérieur est le même que si toute la charge était au centre. |
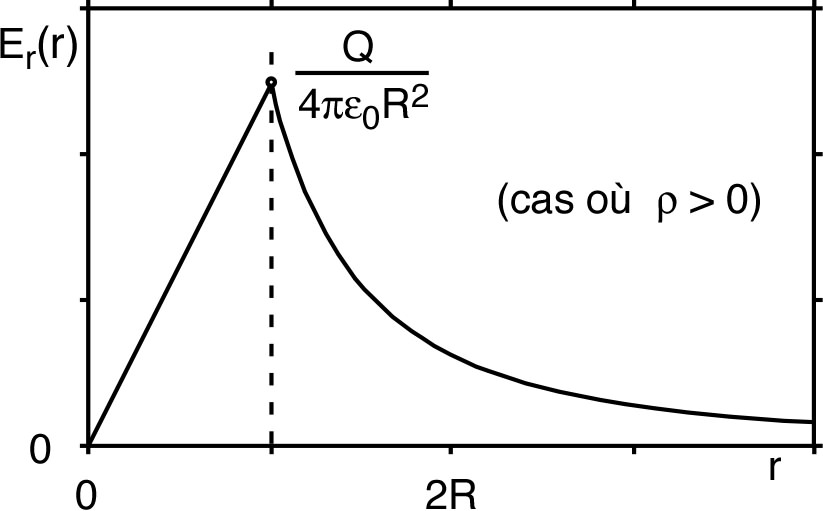
| ◊ |
pour : (en choisissant ) ; |
| ◊ | pour : (par continuité ). |
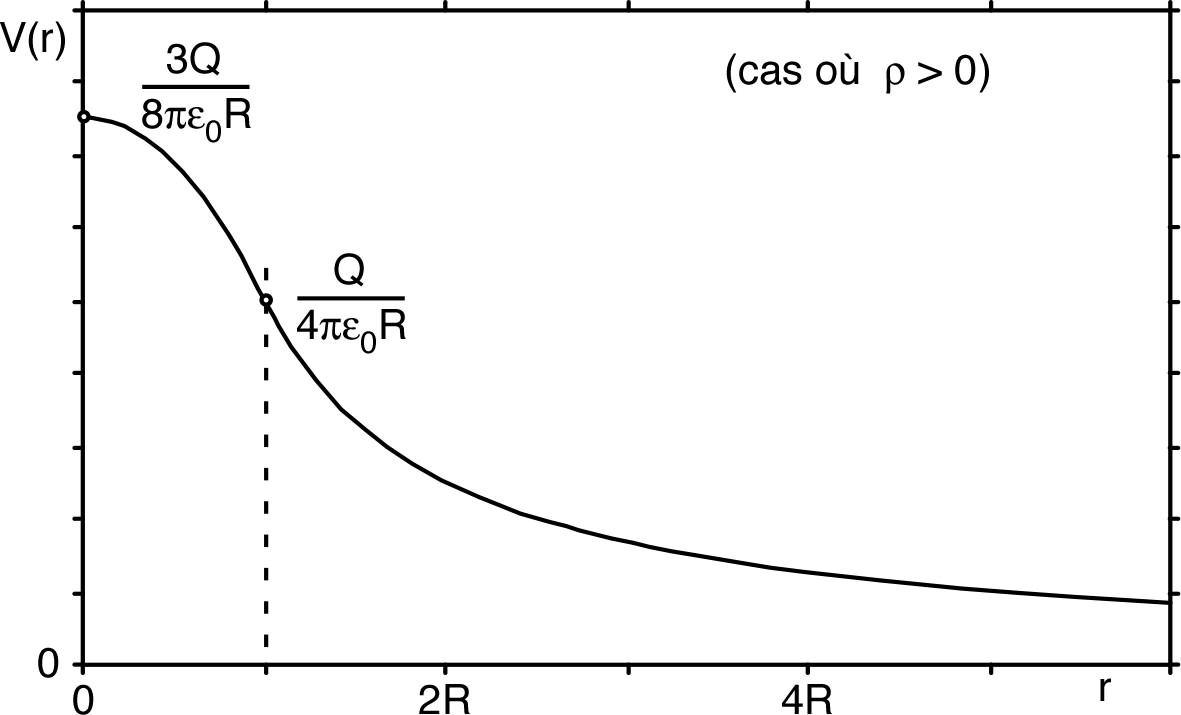
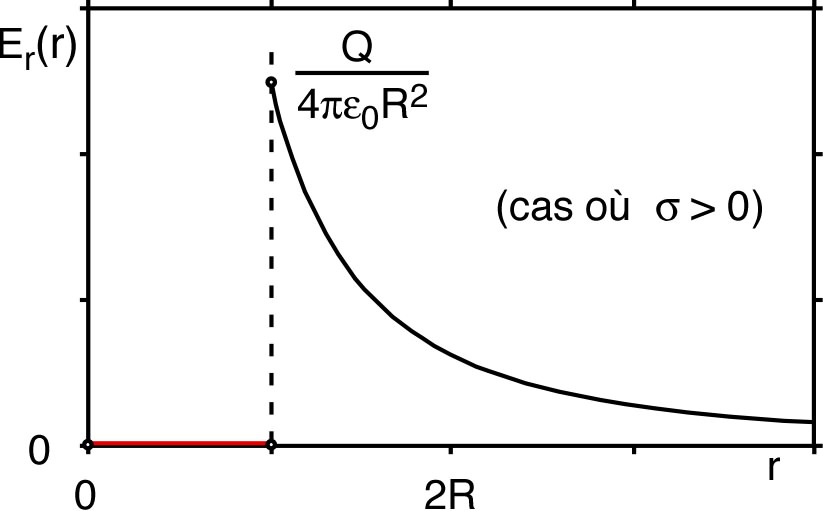
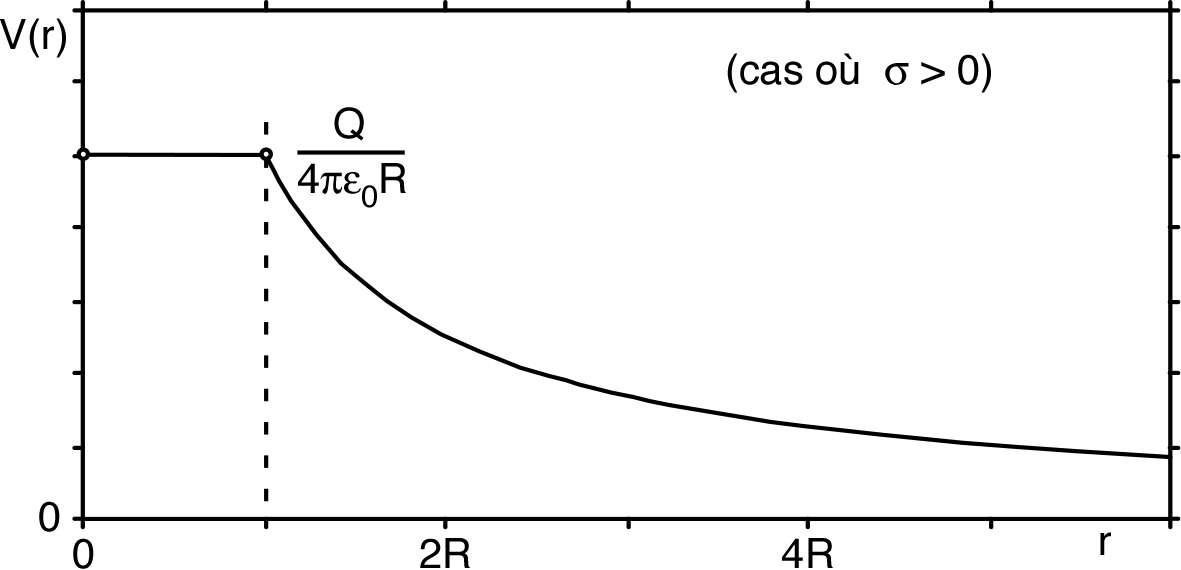
| ☞ remarque : de manière générale, une distribution surfacique des charges donne un champ électrostatique discontinu, mais un potentiel continu. |
| Ce modèle est toutefois souvent trop
simpliste : le résultat du calcul complet dépend de la façon
dont on fait tendre le plan vers l'infini. • Pour un plan “infini”, avec une densité surfacique uniforme :
|
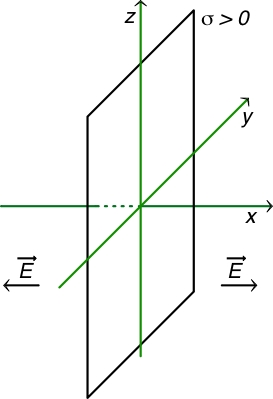 |
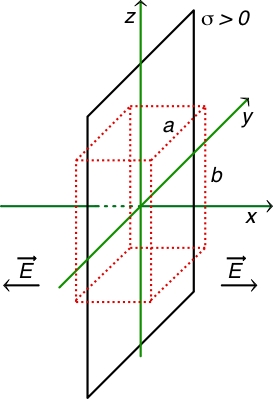
• Avec le modèle du plan “infini”, pour un
“parallélépipède de Gauss” symétrique, le flux sortant se
limite a celui à travers les faces parallèles au plan ;
Pour un plan réel (fini) l'expression de reste raisonnablement valable pour et , dans la mesure où on peut supposer négligeable de flux “latéral”. Mais il peut exister des composantes et non négligeables et ici inconnues. |
 |
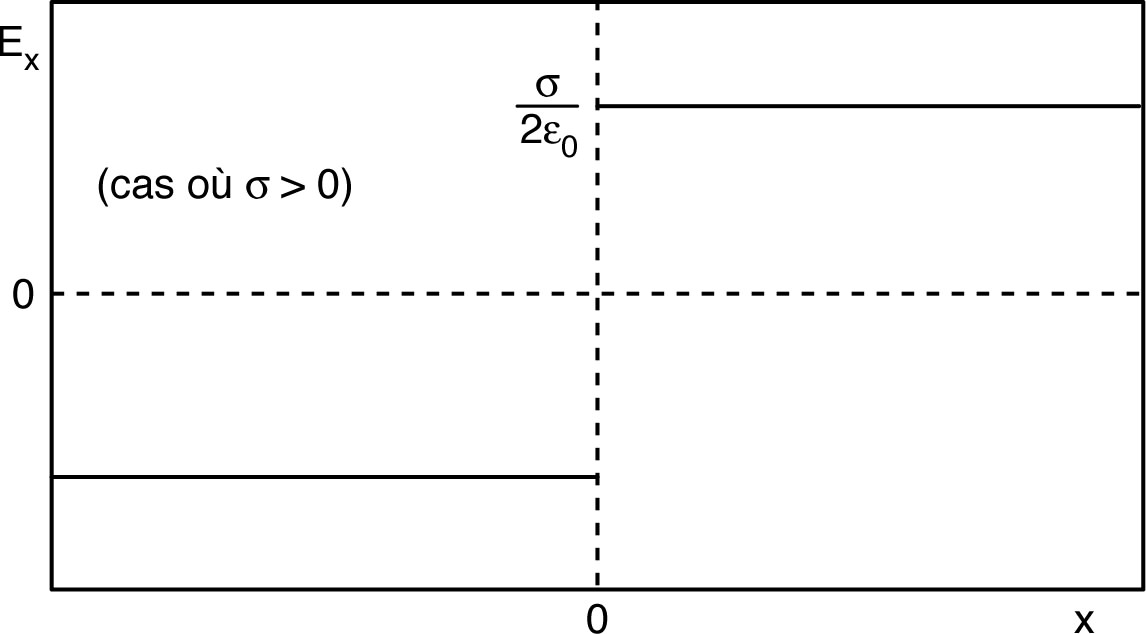
| ◊ |
pour : (ici car il y a des charges à l’infini... il faut alors choisir une abscisse de référence arbitraire) ; |
| ◊ | pour : (par continuité). |
| • L'analogie entre le champ coulombien pour une charge ponctuelle et le champ newtonien pour une masse ponctuelle montre que le théorème de Gauss se transpose au calcul du flux gravitationnel en fonction de la répartition de la masse (par exemple selon une masse volumique ) : . |