THÉORÈME DE GAUSS - corrigé des exercices


A. EXERCICES DE BASE

I. Interprétation du flux dans le cas d'un écoulement

1. • Si toutes les particules ont la même vitesse v→\overset{→}{v} , celles qui traversent une section du tuyau pendant un temps tt sont celles initialement “en amont” de la section considérée, à une distance inférieure à  𝓁=vt𝓁=v \:t .  Cela correspond à un volume :  𝒱=𝓁S=πR2vt𝒱=𝓁 \:S=π \:R^2 \: v \:t  ;  le débit est donc :  D=𝒱t=πR2v\displaystyle D=\frac{𝒱}{t}=π \:R^2 \: v .

2. • Dans le cas précédent, on avait :  D=Sv=S→∙v→D=S \:v=\overset{→}{S}∙\overset{→}{v}  ce qui correspond au flux de v→\overset{→}{v} à travers la section considérée.
• Il en est de même ici pour chaque “couronne” de section infinitésimale de rayon rr et de largeur drdr , puisque la vitesse peut y être considérée comme uniforme :  dD=dS→∙v→(r)=2πrv(r)drdD=d\overset{→}{S}∙\overset{→}{v}(r)=2π \:r \:v(r) \:dr .  Au total :  D=∫v→∙dS→=2πa∫(R2−r2)rdr=2πa.(R42−R44)=πaR42\displaystyle D=∫\overset{→}{v}∙d\overset{→}{S}=2π \:a\, ∫ (R^2-r^2 ) \: r \:dr=2π \:a .\left(\frac{R^4}{2}-\frac{R^4}{4}\right)=π \:a \:\frac{R^4}{2}  ;  ceci correspond effectivement au flux de v→\overset{→}{v} à travers la section du tuyau.


II. Vecteur surface d'un contour orienté

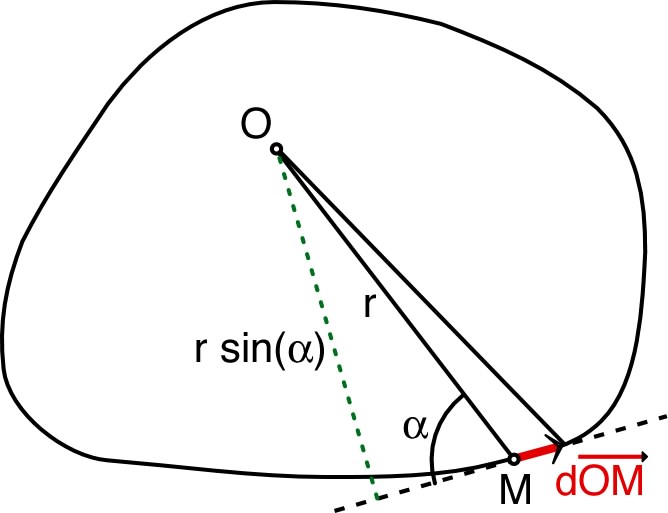
1. • La différentielle dOM⟶d\overset{⟶}{OM} ne dépend pas de l’origine OO , pourvu que ce soit un point fixe ; démontrer l’invariance de l’intégrale se ramène donc à montrer que (pour un contour fermé) la variation est nulle :

 ∫COO′⟶×dOM⟶=OO′⟶×∫CdOM⟶=OO′⟶×0→=0→∫_C \:\overset{⟶}{OO'} × d\overset{⟶}{OM}=\overset{⟶}{OO'} ×∫_C \:d\overset{⟶}{OM}=\overset{⟶}{OO'} × \overset{→}{0}=\overset{→}{0} .

2. • Pour un contour plan, on peut choisir un point OO dans ce plan, à l’intérieur de la zone délimitée par CC . Le vecteur élémentaire  12OM⟶×dOM⟶\frac{1}{2} \overset{⟶}{OM} × d\overset{⟶}{OM}  est alors un vecteur orthogonal au plan, dans le sens positif associé au sens de rotation positif sur CC (orientation du vecteur n→\overset{→}{n} ) et dont la norme est l’aire  dS=12rsin(α)d𝓁dS=\frac{1}{2} r \: \sin(α) \: d𝓁  “balayée” par OM⟶\overset{⟶}{OM} lors de la variation dOM⟶d\overset{⟶}{OM} .
• Ce vecteur est donc un élément d’aire dS→d\overset{→}{S} et l’intégrale est donc égale au vecteur surface S→\overset{→}{S} .
Gauss_cor_Im/Gauss_cor_Im1.jpg

3. • Pour un contour infinitésimal délimitant un élément de surface dS→d\overset{→}{S} ,  les questions précédentes montrent que l’intégrale donne un vecteur infinitésimal :  dA→=dS→d\overset{→}{A}=d\overset{→}{S}  (pour des surfaces “ordinaires” comme celles utilisées en physique, un élément de surface infinitésimal peut être considéré comme plan par passage à la limite).
• Si ensuite on somme les éléments dS→d\overset{→}{S} sur une surface ΣΣ , l’intégrale définissant le vecteur A→\overset{→}{A} total est encore la somme des intégrales élémentaires puisque les intégrations sur les “contours” intérieurs se compensent.

Gauss_cor_Im/Gauss_cor_Im2.jpg

Par suite on obtient ainsi :  A→=∬ΣdS→\overset{→}{A}=∬_Σ \:d\overset{→}{S} ,  vecteur qu’on peut considérer comme “vecteur surface” S→\overset{→}{S} .


III. Extremums du potentiel


 • Supposons que le potentiel soit maximum (éventuellement maximum relatif) en un point MM , alors il existe un voisinage 𝒱𝒱 de MM tel que le potentiel  V(M)V(M)  y soit un maximum absolu, donc tel que toutes les lignes de champ soient sortantes, donc tel que le flux sortant soit strictement positif.
• Dans ce cas  Φ=Qintε0>0\displaystyle Φ=\frac{Q_{int}}{ε_0} >0  implique qu’il y a des charges dans ce voisinage. Si on considère alors une suite de tels voisinages, de plus en plus petits, dont l’intersection soit réduite à MM , on aboutit à la conclusion qu’il y a forcément une charge en MM .
◊ remarque : on ne peut pas envisager une suite de charges ponctuelles dont MM , sans charge, soit un point adhérent, car la quantification de la charge imposerait alors que la charge totale soit infinie dans un domaine fini de l’espace, ce qui n’est pas physiquement réalisable.


IV. Limites de validité du théorème de Gauss

1. • L'invariance par translation montre que le champ est uniforme.
• L'invariance par symétrie plane montre que la composante normale du champ doit changer de sens d'un côté à l'autre d'un plan (quelconque), donc doit être nulle.
• La seule façon de rendre ces propriétés compatibles est que le champ soit nul en tout point.

2. • En raisonnant avec seulement la symétrie sphérique par rapport à un point OO donné (quelconque), le champ est radial par rapport à OO . L'application du théorème de Gauss sur une sphère centrée en OO donne :  4πr2Er(r)=Qintε0=43πr3ρε0\displaystyle 4π \:r^2 \: E_r (r)=\frac{Q_{int}}{ε_0} =\frac{4}{3} π \:r^3 \,\frac{ρ}{ε_0}   ;  ainsi :  Er(r)=r3ρε0\displaystyle E_r (r)=\frac{r}{3} \frac{ρ}{ε_0}   généralement non nul (donc faux).
• La contradiction vient du fait que le théorème de Gauss est démontré pour une répartition de charges sans faire intervenir d'infinis dans la sommation. La compensation des effets des flux entrants et sortants de la surface de Gauss impose alors que seules les charges intérieures ont une influence.
• Pour ρρ uniforme dans tout l'espace (hypothèse en réalité physiquement contradictoire) la compensation d'infinités de contributions (jusqu'à l'infini) de flux entrants et sortants de la surface de Gauss fait intervenir une intégrale  (∞−∞)(∞-∞)  indéterminée.
◊ remarque : pour une densité uniforme entre deux plans parallèles “infinis”, ou pour une densité uniforme dans un cylindre “infini”, les charges “à l'infini” sont vues sous un angle solide négligeable, ce qui permet de contourner cette contradiction (mais il reste à justifier les “infinis”).


V. Mouvement circulaire et champ électrostatique

1. • D'après la symétrie sphérique, le champ électrostatique est radial et la composante radiale ne dépend que de rr :  E→=Er(r)u→r\overset{→}{E}=E_r (r) \:\overset{→}{u}_r .  Par suite, le flux à travers une “surface de Gauss” sphérique, de rayon rr et centrée en OO , est :  Φ=∫E→∙dS→=∫ErdS=4πr2Er=Qintε0\displaystyle Φ=∫ \overset{→}{E}∙d\overset{→}{S}=∫ E_r\: dS=4π \:r^2 \: E_r=\frac{Q_{int}}{ε_0}  d'où on déduit :  Er=Qint4πε0r2\displaystyle E_r=\frac{Q_{int}}{4π \:ε_0\: r^2} .
• Par ailleurs, pour  r≤Rr≤R  la charge intérieure est :

 Qint=∭ρ(r)dτ=4πρ0∫0re−αr′r′2dr′=4πρ0∂2(∫0re−αr′dr′)∂α2\displaystyle Q_{int}=∭ ρ(r) \: dτ=4π \:ρ_0 \, ∫_0^r \mathrm{e}^{-αr'} \: {r'}^2 \: dr'=4π \:ρ_0 \: \frac{∂^2 \left(∫_0^r \:\mathrm{e}^{-αr'} \:dr'\right)}{{∂α}^2}   ;
Qint=4πρ0∂2(1−e−αrα)∂α2=4πρ02−e−αr.(2+2rα+r2α2)α3\displaystyle Q_{int}=4π \:ρ_0 \: \frac{∂^2 \left(\frac{1-\mathrm{e}^{-αr}}{α}\right)}{{∂α}^2} =4π \:ρ_0 \: \frac{2-e^{-αr}.(2+2rα+r^2 α^2 )}{α^3}  .
• De même, pour  r≥Rr≥R :

 Qint=∭ρ(r)dτ=4πρ0∂2(∫0Re−αr′dr′)∂α2=4πρ02−e−αR.(2+2Rα+R2α2)α3\displaystyle Q_{int}=∭ ρ(r) \: dτ=4π \:ρ_0 \: \frac{∂^2 \left(∫_0^R \,\mathrm{e}^{-αr'} \: dr'\right)}{{∂α}^2} =4π \:ρ_0 \: \frac{2-\mathrm{e}^{-αR}.(2+2Rα+R^2 α^2 )}{α^3}  .

2. • Pour un champ électrique radial, il s'agit d'un mouvement à force centrale. Ce mouvement est plan et vérifie la loi des aires :  r2ω=Cr^2 \:ω=C  est une constante. Pour un mouvement circulaire, la force électrique ne travaille pas et la vitesse est de norme vv constante, ce qui est cohérent avec  r=r0r=r_0  et  ω=vr0\displaystyle ω=\frac{v}{r_0}  constants.
◊ remarque : l'énoncé précise que  Qρ0<0Q \:ρ_0<0  pour que la force soit attractive.
• L'accélération est alors radiale :  ar=−ω2r0=QErm\displaystyle a_r=-ω^2 \: r_0=\frac{Q \:E_r}{m} , d'où on déduit :

T=2πω=2π−mr0QEr=2πε0mr03α3Qρ0.(2−e−αr0.(2+2r0α+r02α2))\displaystyle T=\frac{2π}{ω}=2π \:\sqrt{-\frac{m \:r_0}{Q \:E_r}}=2π \:\sqrt{\frac{ε_0 \: m \:r_0^{\:3} α^3}{Q \:ρ_0.\left(2-\mathrm{e}^{-αr_0}.\left(2+2r_0α+r_0^{\:2} α^2\right)\right)}} .


VI. Détermination d'une répartition de charges


 • Pour un point intérieur à la boule, par symétrie, le champ est radial et la composante radiale ne dépend que de rr :  E→=Er(r)u→r\overset{→}{E}=E_r (r) \:\overset{→}{u}_r .
• Le théorème de Gauss donne :  Φ=∫E→∙dS→=∫ErdS=4πr2Er=Qintε0\displaystyle Φ=∫ \overset{→}{E}∙d\overset{→}{S}=∫ E_r \: dS=4π \:r^2 \: E_r=\frac{Q_{int}}{ε_0}  d'où  Er=Qint4πε0r2\displaystyle E_r=\frac{Q_{int}}{4π \:ε_0 \: r^2} .  Or, on veut obtenir un champ de la forme :  E→=E0OM⟶r=E0u→r\displaystyle \overset{→}{E}=E_0 \: \frac{\overset{⟶}{OM}}{r}=E_0 \: \overset{→}{u}_r  ;  ceci impose donc :  Qint=4πε0E0r2Q_{int}=4π \:ε_0 \: E_0 \: r^2 .
• En utilisant le volume “élémentaire”  dτ=r2sin(θ)drdθdϕdτ=r^2 \: \sin(θ) \: dr \:dθ \:dϕ  des coordonnées sphériques, la charge intérieure à la sphère de Gauss peut par ailleurs s’écrire sous la forme :

 Qint=∭ρ(r)dτ=(∫0πsin(θ)dθ).(∫02πdϕ).(∫0rρr2dr)=4π∫0rρr2drQ_{int}=∭ ρ(r)\: dτ=\left(∫_0^π \:\sin(θ) \: dθ \right).\left(∫_0^{2π} \:dϕ\right).\left(∫_0^r \:ρ \: r^2 \: dr\right)=4π\: ∫_0^r \:ρ \:r^2 \: dr .
• On en déduit par comparaison :  ε0E0r2=∫0rρr2drε_0 \: E_0 \: r^2=∫_0^r \:ρ \: r^2 \: dr ,  puis en dérivant :  2ε0E0r=ρr22 \,ε_0 \: E_0 \: r=ρ \:r^2  et donc :  ρ(r)=2ε0E0r\displaystyle ρ(r)=\frac{2 \,ε_0 \: E_0}{r} .
• La charge totale est alors :  Q=4π∫0Rρr2dr=4πε0E0R2Q=4π \:∫_0^R \:ρ \: r^2 \: dr=4π \:ε_0 \: E_0 \: R^2  (il n’est pas nécessaire d’intégrer, il suffit de reprendre la première expression).
• D’après le théorème de Gauss (compte tenu des symétries), le champ à l’extérieur est le même que celui créé par une charge QQ ponctuelle placée à l’origine :  E→=Er(r)u→r\overset{→}{E}=E_r (r)\: \overset{→}{u}_r  avec  Er=Q4πε0r2\displaystyle E_r=\frac{Q}{4π \:ε_0 \: r^2} .


VII. Potentiel de Yukawa

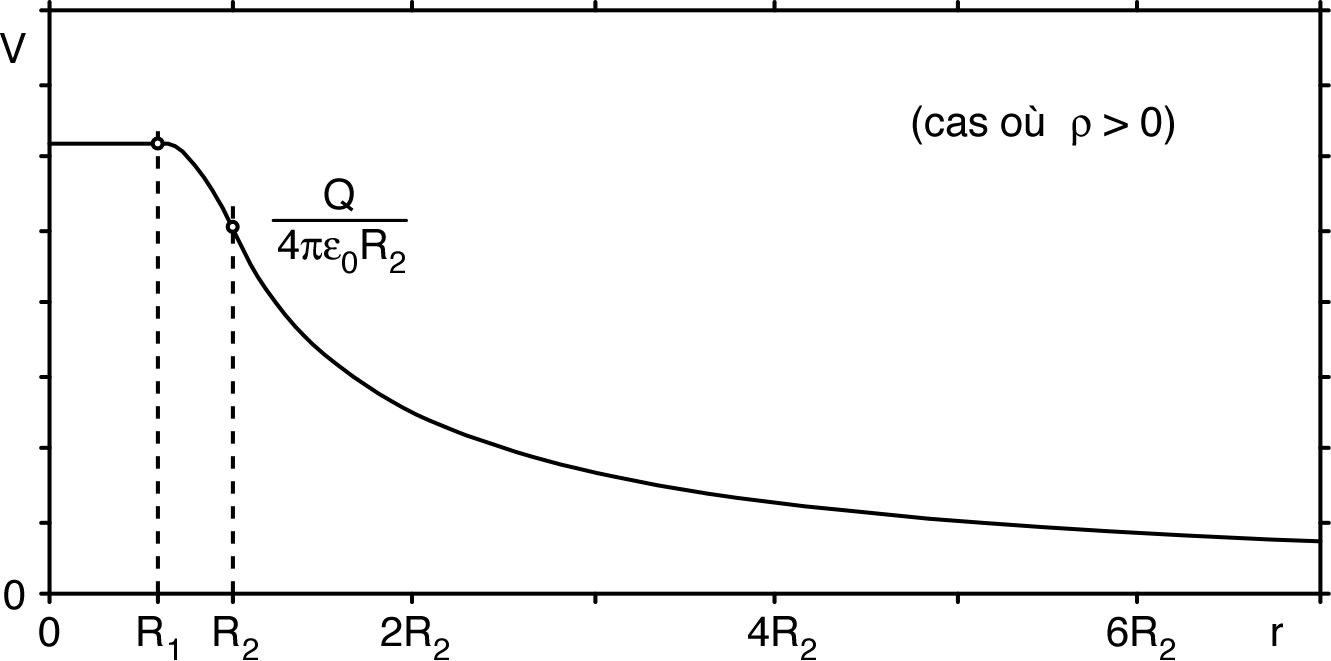
1. • D’après la symétrie sphérique, le champ E→\overset{→}{E} est radial et la coordonnée radiale ne dépend que de rr :

 E→=Er(r)u→r\overset{→}{E}=E_r (r)\: \overset{→}{u}_r  et  Er(r)=−∂V∂r=e−r/𝒶q4πε0r2(1+r𝒶)\displaystyle E_r (r)=-\frac{∂V}{∂r}=\mathrm{e}^{-r/𝒶} \; \frac{q}{4π \:ε_0 \: r^2} \: \left(1+\frac{r}{𝒶}\right) .
• Pour  r≪𝒶r≪𝒶  on obtient :  V(r)≈q4πε0r\displaystyle V(r)≈\frac{q}{4π \:ε_0 \: r}  et  Er(r)≈q4πε0r2\displaystyle E_r (r)≈\frac{q}{4π \:ε_0 \: r^2}  ;  on retrouve ainsi un potentiel et un champ coulombiens.
• Pour  r≫𝒶r≫𝒶  on obtient V(r)V(r) et Er(r)E_r (r) quasi nuls (la décroissance exponentielle est très rapide) ;  la grandeur “𝒶𝒶” est donc une distance caractéristique de la “portée” du potentiel et du champ correspondants.

2. • Le théorème de Gauss donne alors :  Φ=∫E→∙dS→=∫ErdS=4πr2Er=e−r/𝒶qε0(1+r𝒶)\displaystyle Φ=∫ \overset{→}{E}∙d\overset{→}{S}=∫ E_r \: dS=4π \:r^2 \: E_r=\mathrm{e}^{-r/𝒶} \; \frac{q}{ε_0} \: \left(1+\frac{r}{𝒶}\right) .
• On en déduit la charge intérieure :  Qint(r)=ε0Φ=e−r/𝒶q.(1+r𝒶)\displaystyle Q_{int} (r)=ε_0 \: Φ = \mathrm{e}^{-r/𝒶} \; q .\left(1+\frac{r}{𝒶}\right) .
• Par ailleurs, la symétrie sphérique impose que la densité volumique de charge peut être considérée comme uniforme dans une couche sphérique entre rr et  r+drr+dr :  ρ(r)=dQintdτ\displaystyle ρ(r)=\frac{dQ_{int}}{dτ}  avec  dτ=4πr2drdτ=4π \:r^2 \: dr .  On en déduit :  ρ(r)=−e−r/𝒶q4πr𝒶2\displaystyle ρ(r)=-\mathrm{e}^{-r/𝒶} \; \frac{q}{4π \:r \:𝒶^2} .
• La caractéristique essentielle de cette répartition est qu’elle correspond à une densité de charge “partout” négative, alors que la charge intérieure à la sphère de Gauss est positive pour tout rr . Ceci ne peut correspondre qu’à une charge centrale positive ponctuelle, compensée en partie par une densité volumique négative (qui ne décrit que les charges réparties).
◊ remarque : on peut vérifier que  Qint(r)→qQ_{int} (r)→q  pour  r→0 r→0  (charge centrale) ; par ailleurs  Qint(r)→0Q_{int} (r)→0  pour  r→∞r→∞  (la charge négative totale compense exactement la charge positive centrale).


VIII. Champ dans une cavité
• Compte tenu de l’additivité des champs électrostatiques, le système étudié est équivalent à la superposition virtuelle d’une boule pleine, de centre OO et de rayon RR , portant une distribution volumique ρρ , avec une autre boule pleine, de centre O′O' et de rayon 𝒶𝒶 , portant une distribution volumique −ρ-ρ .
• Dans la boule (pleine) de rayon RR , le champ est radial et la composante radiale ne dépend que de rr :  E→=Er(r)u→r\overset{→}{E}=E_r (r) \:\overset{→}{u}_r .  Le théorème de Gauss donne :

 Φ=∫E→∙dS→=∫ErdS=4πr2Er=Qintε0\displaystyle Φ=∫\overset{→}{E}∙d\overset{→}{S}=∫ E_r \: dS=4π \:r^2 \: E_r=\frac{Q_{int}}{ε_0} .

Gauss_cor_Im/Gauss_cor_Im3.jpg
• On en déduit :  Er=Qint4πε0r2\displaystyle E_r=\frac{Q_{int}}{4π \:ε_0 \: r^2}  avec :  Qint=43πr3ρQ_{int}=\frac{4}{3} π \:r^3 \: ρ ,  c’est-à-dire :  Er=ρ3ε0r\displaystyle E_r=\frac{ρ}{3 \:ε_0} \: r .
• Le calcul est analogue pour la seconde boule ; on obtient donc au total pour un point intérieur à la cavité :  E→=ρ3ε0ru→r−ρ3ε0r′u→r′\overset{→}{E}=\frac{ρ}{3 \:ε_0} \: r \:\overset{→}{u}_r-\frac{ρ}{3 \:ε_0} \: r' \:\overset{→}{u}'_r .
• Mais  ru→r=OM⟶r \:\overset{→}{u}_r=\overset{⟶}{OM}  et  r′u→r′=O′M→r' \:\overset{→}{u}'_r=\overset{→}{O'M}  donc :  E→=ρ3ε0(OM⟶−O′M→)=ρ3ε0OO′→\displaystyle \overset{→}{E}=\frac{ρ}{3 \:ε_0} \: \left(\overset{⟶}{OM}-\overset{→}{O'M} \right)=\frac{ρ}{3 ε_0} \: \overset{→}{OO'}  (champ uniforme).


IX. Potentiel d'une couche chargée


 • Pour une “couche sphérique” entre deux rayons R1R_1 et R2R_2 , chargée d’une densité ρρ uniforme :
◊
 par symétrie selon le rayon, le champ est radial :  E→=Er(r,θ,ϕ)u→r\overset{→}{E}=E_r (r,θ,ϕ) \: \overset{→}{u}_r  ;
◊ par invariance des charges selon θθ et ϕϕ , la coordonnée radiale du champ ne dépend que de rr :  Er(r,θ,ϕ)=Er(r)E_r (r,θ,ϕ)=E_r (r)  ;
◊ le flux sortant à travers une “sphère de Gauss” concentrique est :  Φ(r)=4πr2Er(r)=Qint(r)ε0\displaystyle Φ(r)=4π \:r^2 \: E_r (r)=\frac{Q_{int} (r)}{ε_0}  ;
◊ pour  r≤R1r≤R_1 :  Qint(r)=0Q_{int} (r)=0  et  Er(r)=0E_r (r)=0  ;
◊ pour  R1≤r≤R2R_1≤r≤R_2 :  Qint(r)=43πρ.(r3−R13)Q_{int} (r)=\frac{4}{3} π \:ρ.\left(r^3-R_1^{\:3} \right)   et   Er(r)=ρ3ε0r3−R13r2\displaystyle E_r (r)=\frac{ρ}{3 \,ε_0} \, \frac{r^3-R_1^{\:3}}{r^2}  ;
◊ pour  r≥R2r≥R_2 :  Qint(r)=Q=43πρ.(R23−R13)Q_{int} (r)=Q=\frac{4}{3} π \:ρ.\left(R_2^{\:3}-R_1^{\:3} \right)   et   Er(r)=Q4πε0r2\displaystyle E_r (r)=\frac{Q}{4π \:ε_0 \: r^2} .

Gauss_cor_Im/Gauss_cor_Im4.jpg
 Gauss_cor_Im/Gauss_cor_Im5.jpg

◊ remarque : on constate en particulier que, pour une distribution à symétrie sphérique, le champ extérieur est le même que si toute la charge était concentrée au centre.

• On peut ensuite en déduire le potentiel :
◊
 pour  r≥R2r≥R_2 :  V(r)=Q4πε0r\displaystyle V(r)=\frac{Q}{4π \:ε_0 \: r}   (en choisissant  V∞=0V_∞=0 ) ;
◊ pour  R1≤r≤R2R_1≤r≤R_2 :  V(r)=ρ3ε0−r3+3rR22−2R132r\displaystyle V(r)=\frac{ρ}{3 \:ε_0} \: \frac{-r^3+3 \,r \:R_2^{\:2}-2 \,R_1^{\:3}}{2 \,r}  (avec  V(R2)=Q4πε0R2\displaystyle V(R_2)=\frac{Q}{4π \:ε_0 \: R_2}  par continuité) ;
◊ pour  r≤R1r≤R_1 :  V(r)=ρ2ε0(R22−R12)\displaystyle V(r)=\frac{ρ}{2 \,ε_0} \: \left(R_2^{\:2}-R_1^{\:2} \right)  (par continuité pour  r=R1r=R_1 ).
◊ remarque : d’une manière générale, une distribution volumique continue des charges donne un champ électrostatique continu, donc un potentiel continu à dérivées continues.

Gauss_cor_Im/Gauss_cor_Im6.jpg


X. Champ créé par une couche chargée

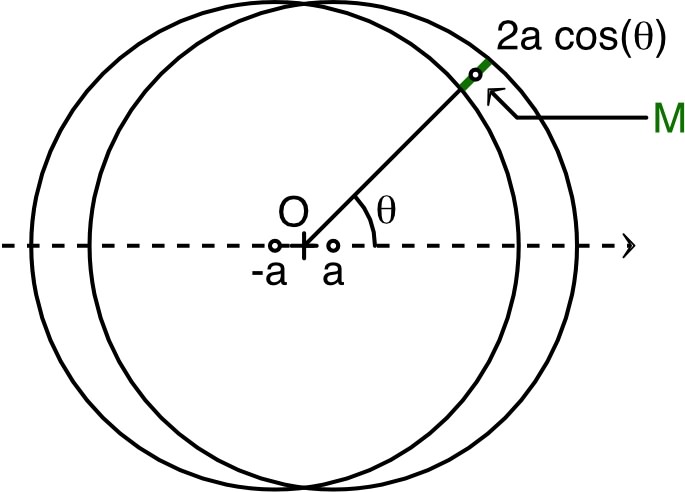
1. • Dans la zone d’intersection des deux boules, les charges se compensent ; on est donc ramené à considérer leur zone de “différence” (entre les deux sphères).
• En notant O1O_1 et O2O_2 les centres des sphères, le segment de la droite (OM)(OM) qui mesure l’épaisseur correspond à la projection sur OM⟶\overset{⟶}{OM} du décalage O1O2→\overset{→}{O_1 O_2} :  ℯ≈2𝒶|cos(θ)|ℯ≈2 \,𝒶 \:\left|\cos(θ) \right| .
• Or l'épaisseur reste faible  (𝒶≪R𝒶≪R)  donc la distribution de charge peut être représentée par une densité surfacique  σ≈±ρℯ=2𝒶ρcos(θ)σ≈±ρ \:ℯ=2 \:𝒶 \:ρ \: \cos(θ)  (le signe de cos(θ)\cos(θ) prend en compte le signe de  −ρ<0-ρ<0  à gauche).
Gauss_cor_Im/Gauss_cor_Im7.jpg

2. • Par additivité des champs électrostatiques, le calcul se ramène à celui du champ d’une boule portant une distribution volumique ρρ . Pour un point intérieur à la boule, le champ est radial et la composante radiale ne dépend que de rr :  E→=Er(r)u→r\overset{→}{E}=E_r (r) \: \overset{→}{u}_r .
• Le théorème de Gauss donne :  Φ=∫E→∙dS→=∫ErdS=4πr2Er=Qintε0\displaystyle Φ=∫ \overset{→}{E}∙d\overset{→}{S}=∫ E_r \: dS=4π \:r^2 \: E_r=\frac{Q_{int}}{ε_0}    d'où   Er=Qint4πε0r2\displaystyle E_r=\frac{Q_{int}}{4π \:ε_0 \: r^2}  avec   Qint=43πr3ρQ_{int}=\frac{4}{3} π \:r^3 \: ρ ,  c’est-à-dire :  Er=ρ3ε0r\displaystyle E_r=\frac{ρ}{3 \,ε_0} \: r .
• Le calcul étant analogue pour la seconde sphère pleine, on obtient au total pour un point intérieur :  E→=ρ3ε0r1u→r1−ρ3ε0r2u→r2\displaystyle \overset{→}{E}=\frac{ρ}{3 \,ε_0} \: r_1\: \overset{→}{u}_{r_1}-\frac{ρ}{3 \,ε_0} \: r_2 \: \overset{→}{u}_{r_2} .  Mais  r1u→r1=O1M→r_1\: \overset{→}{u}_{r_1}=\overset{→}{O_1 M}  et  r2u→r2=O2M→r_2 \: \overset{→}{u}_{r_2}=\overset{→}{O_2 M}  donc on obtient un champ uniforme :  E→=ρ3ε0(O1M→−O2M→)=ρ3ε0O1O2→\displaystyle \overset{→}{E}=\frac{ρ}{3 \,ε_0} \: \left(\overset{→}{O_1 M}- \overset{→}{O_2 M} \right)=\frac{ρ}{3 \,ε_0} \: \overset{→}{O_1 O_2} . Il en est donc de même pour une sphère chargée d’une densité surfacique de la forme  σ=σ0cos(θ)σ=σ_0 \; \cos(θ)  (il suffit de considérer  ρ=σ02𝒶\displaystyle ρ=\frac{σ_0}{2 \,𝒶} ).


XI. Champ créé par un fil rectiligne “infini”


 • On considère un modèle théorique de fil rectiligne “infini”, chargé d’une densité linéique λλ uniforme :
◊
 par symétrie selon le rayon, le champ est radial :  E→(r,θ,z)=Er(r,θ,z)u→r\overset{→}{E}(r,θ,z)=E_r (r,θ,z) \: \overset{→}{u}_r  ;
◊ par invariance des charges selon θθ et zz , la composante radiale du champ ne dépend que de rr :  Er(r,θ,z)=Er(r)E_r (r,θ,z)=E_r (r)  ;
◊ le flux sortant d’un cylindre coaxial est :  Φ(r)=2πrhEr(r)=Qintε0\displaystyle Φ(r)=2π \:r \:h \:E_r(r)=\frac{Q_{int}}{ε_0}   (flux nul par les bases) ;
◊ pour  r>0r>0 :  Qint(r)=hλQ_{int} (r)=h \:λ   et   Er(r)=λ2πε0r\displaystyle E_r(r)=\frac{λ}{2π \:ε_0 \: r} .

Gauss_cor_Im/Gauss_cor_Im8.jpg
 Gauss_cor_Im/Gauss_cor_Im9.jpg

• On peut ensuite en déduire le potentiel : pour  r>0r>0 :  V(r)=−λ2πε0ln(rr0)\displaystyle V(r)=-\frac{λ}{2π ε_0} \: \ln\left(\frac{r}{r_0} \right)  (on choisit une référence arbitraire en r0r_0 car rr doit rester limité par rapport au fil non réellement “infini”, donc le choix  V∞=0V_∞=0  est impossible).
☞ remarque : le champ et le potentiel tendent vers l’infini aux endroits (ici  r=0r=0 ) où se trouvent des distributions linéiques (ou ponctuelles) de charges.
• La représentation (ci-après à gauche) en coordonnées réduites dans le plan  z=0z=0  peut être comparée au calcul exact par intégration directe pour un fil de longueur LL (on choisit  r0=Lr_0=L ).  On constate que le modèle théorique donne une bonne représentation tant que  r≪Lr≪L .

Gauss_cor_Im/Gauss_cor_Im10a.png
 Gauss_cor_Im/Gauss_cor_Im10b.png

• Mais l'utilisation d'un modèle théorique de fil “infini” pose en réalité le même genre de problèmes que pour un plan infini : la composante radiale du champ est estimée à peu près correctement (sauf à proximité des extrémités du fil réel), mais la composante axiale du champ (non calculée ainsi) n'est généralement pas négligeable. De ce fait le potentiel dépend aussi de zz ; on peut montrer que les équipotentielles sont des ellipsoïdes de révolution ayant les deux extrémités du fil réel comme foyers.
• L'expression exacte est :  V(r)=−λ4πε0ln(r2+(z+L/2)2+r2+(z−L/2)2+Lr2+(z+L/2)2+r2+(z−L/2)2−L)\displaystyle V(r)=-\frac{λ}{4π \:ε_0} \: \ln\left(\frac{\sqrt{r^2+(z+L/2)^2}+\sqrt{r^2+(z-L/2)^2}+L}{\sqrt{r^2+(z+L/2)^2}+\sqrt{r^2+(z-L/2)^2}-L}\right)  ;  on peut comparer (ci-avant à droite) le modèle théorique et le tracé exact pour  z=0,5L/2z=\text{0,5} \:L/2  (en vert) et  z=0,8L/2z=\text{0,8} \:L/2  (en rouge). On constate que la dépendance en rr conserve une pente de même allure, donc le calcul de la composante radiale du champ reste une approximation tolérable, même si la justification n'en est plus valable ; par contre il apparaît une dépendance en zz ,  donc le champ n'est plus radial : il existe une composante axiale non négligeable dès qu'on s'écarte du milieu du fil (l'expression “loin des extrémités” n'est pas assez restrictive).

• En revanche, le modèle théorique “infini” peut s'appliquer acceptablement pour un condensateur cylindrique car, toute charge sur une armature ayant son opposé sur l'autre armature, les contributions  axiales du champ se compensent en bonne approximation.


B. EXERCICE D’APPROFONDISSEMENT

XII. Ion dans un plasma

1. • D'après les symétries (autour d’un ion positif donné), le champ est radial et la coordonnée radiale ne dépend que de rr :  E→=Er(r)u→r\overset{→}{E}=E_r (r) \: \overset{→}{u}_r .  Le flux électrostatique sortant d’une sphère de rayon rr (centrée sur la position de l’ion) est alors :  Φ(r)=∫E→∙dS→=∫ErdS=4πr2Er=Qintε0\displaystyle Φ(r)=∫ \overset{→}{E}∙d\overset{→}{S}=∫ E_r \: dS=4π \:r^2 \: E_r=\frac{Q_{int}}{ε_0} .
• Pour une couche sphérique d’épaisseur drdr (entre  rr  et  r+drr+dr ), on obtient un flux sortant :

 dΦ(r)=Φ(r+dr)−Φ(r)=dQintε0\displaystyle dΦ(r)=Φ(r+dr)-Φ(r)=\frac{dQ_{int}}{ε_0}  .
• Ceci peut s’écrire :  4πd(r2Er)=ρ(r)ε0dτ(r)\displaystyle 4π \:d(r^2 \: E_r)=\frac{ρ(r)}{ε_0} \: dτ(r)  où  dτ(r)=4πr2drdτ(r)=4π \:r^2 \: dr  est le volume infinitésimal entre les sphères de rayons  rr  et  r+drr+dr .  Or, d’après l’énoncé :  ρ(r)=q.[ni(r)−ne(r)]ρ(r)=q.\left[n_i (r)-n_e (r)\right]  ;  en outre  Er(r)=−dVdr\displaystyle E_r (r)=-\frac{dV}{dr}  ;  par suite :  d[r2dVdr]=qn0r2.[eqV(r)/kT−e−qV(r)/kT]dr\displaystyle d\left[r^2 \: \frac{dV}{dr}\right]=q \:n_0 \: r^2.\left[\mathrm{e}^{qV(r)/kT} - \mathrm{e}^{-qV(r)/kT} \right] \: dr .
• On aboutit donc à l’équation différentielle :  d2Vdr2+2rdVdr=qn0.[eqV/kT−e−qV/kT]\displaystyle \frac{d^2 V}{{dr}^2} +\frac{2}{r} \: \frac{dV}{dr}=q \:n_0 .\left[\mathrm{e}^{qV/kT} - \mathrm{e}^{-qV/kT} \right] .

2. • Pour  kT≫qVk \:T≫q \:V  on peut utiliser :  e±qV/kT≈1±qVkT\displaystyle \mathrm{e}^{±qV/kT}≈1±\frac{q \:V}{k \:T}  d’où :  [eqV/kT−e−qV/kT]≈2qVkT\displaystyle \left[\mathrm{e}^{qV/kT} - \mathrm{e}^{-qV/kT} \right]≈2 \: \frac{q \:V}{k \:T} .  L’équation différentielle devient alors :  d2Vdr2+2rdVdr−2q2n0kTV≈0\displaystyle \frac{d^2 V}{{dr}^2} +\frac{2}{r} \: \frac{dV}{dr}-\frac{2 \,q^2 \: n_0}{k \:T} \: V≈0 .

3. • En utilisant  U(r)=rV(r)U(r)=r \:V(r)  on obtient :  V=Ur\displaystyle V=\frac{U}{r}   ;   dVdr=1rdUdr−Ur2\displaystyle \frac{dV}{dr}=\frac{1}{r} \: \frac{dU}{dr}-\frac{U}{r^2}    ;   d2Vdr2=1rd2Udr2−2r2dUdr+2r3U\displaystyle \frac{d^2 V}{{dr}^2} =\frac{1}{r} \: \frac{d^2 U}{{dr}^2} -\frac{2}{r^2} \: \frac{dU}{dr}+\frac{2}{r^3} \: U .  Ainsi l’équation différentielle s’écrit sous forme linéaire :  d2Udr2−2q2n0kTU≈0\displaystyle \frac{d^2 U}{{dr}^2} -\frac{2 \,q^2 \: n_0}{k \:T} \: U≈0 .
• En posant  α=q2n0kT\displaystyle α=q \:\sqrt{\frac{2 \,n_0}{k \:T}}  on obtient :  d2Udr2−α2U≈0\displaystyle \frac{d^2 U}{{dr}^2} -α^2 \: U≈0  dont les solutions sont de la forme générale :  U=Aeαr+Be−αrU=A \:\mathrm{e}^{αr} + B \:\mathrm{e}^{-αr}  où  AA et B∈ℝB∈ℝ  sont des constantes d’intégration. Mais le potentiel  V=Ur\displaystyle V=\frac{U}{r}  doit tendre vers une constante à grande distance (champ nul par compensation des charges à grande échelle), par suite  A=0A=0  et  V=Bre−αr\displaystyle V=\frac{B}{r} \: \mathrm{e}^{-αr} .
• Par ailleurs, pour  r≈0r≈0  (au voisinage immédiat de l’ion considéré), on doit retrouver  Er≈q4πε0r2\displaystyle E_r≈\frac{q}{4π \:ε_0 \: r^2}  (champ d’une charge ponctuelle) ; c’est-à-dire :  −dVdr=B.(αr+1r2)e−αr≈q4πε0r2\displaystyle -\frac{dV}{dr}=B.\left(\frac{α}{r}+\frac{1}{r^2} \right) \: \mathrm{e}^{-αr}≈\frac{q}{4π \:ε_0 \: r^2} .  Cette condition impose  B=q4πε0\displaystyle B=\frac{q}{4π \:ε_0}  d’où finalement :  V=q4πε0re−αr\displaystyle V=\frac{q}{4π \:ε_0 \: r} \: \mathrm{e}^{-αr} .
◊ remarque : on retrouve  V≈q4πε0r\displaystyle V≈\frac{q}{4π \:ε_0 \: r}  pour  r≈0 r≈0 ,  mais il est plus prudent de considérer la limite du champ, plutôt que celle du potentiel, car ce dernier est défini à une constante près, difficile à choisir ici sans ambiguïté.