E.M.VII - FORCES MAGNÉTIQUES

Loi de Laplace

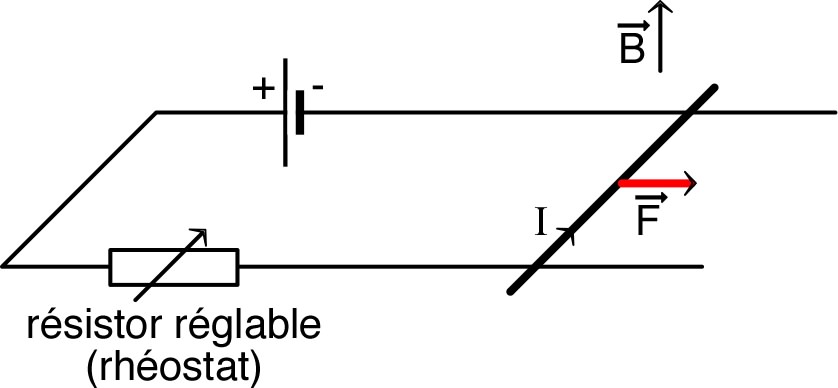
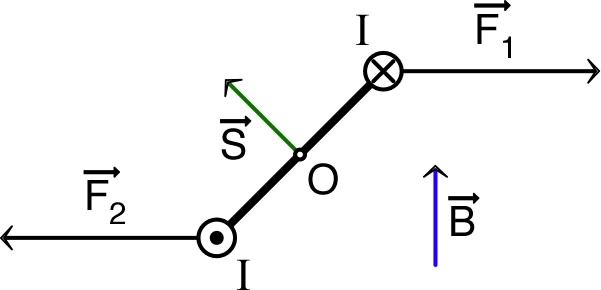
• Dans un champ

\overset{→}{B}

extérieur, la somme des forces de Lorentz

\overset{→}{F}=q \:\overset{→}{v}×\overset{→}{B}

appliquées aux charges mobiles donne, sur chaque élément de circuit

\overset{→}{d𝓁}

parcouru par un courant

I

, une force globale

d\overset{→}{F}=I \:\overset{→}{d𝓁}×\overset{→}{B}

Application à la mesure d’un champ magnétique

• La loi de Laplace appliquée à la balance de Cotton permet de mesurer un champ magnétique localisé dans une zone limitée de l'espace (ou de mesurer l’intensité d’un courant si on connaît le champ magnétique).

• Par rapport à l’axe passant par

O

, les seules forces de moment non nul sont

\overset{→}{F}_1

\overset{→}{P}

; en notant

d

d'

les longueurs des bras du fléau, avec

𝓁=AC

, on obtient la condition d’équilibre :

I \:𝓁 \:B \:d=m \:g \:d'

d’où on peut déduire

B

(ou le courant

I

).

◊ remarque : ce dispositif particulier suppose que

\overset{→}{B}

est horizontal.

📖 exercice n° I.

Application au moteur électrique à courant continu

• La loi de Laplace s’applique à divers types de moteurs. Par exemple, en utilisant un aimant dont l'entrefer est de forme appropriée, on crée un champ magnétique radial à la périphérie d'un cylindre de fer “doux” (qui s'aimante mais ne conserve pas l'aimantation).

Le cylindre est entouré de spires conductrices rectangulaires. Un “collecteur” fait passer un courant

I

dans chaque spire parallèle à

\overset{→}{B}

(toutes sauf celles dans la zone de l'entrefer où il y a retournement de

\overset{→}{B}

).

Chaque spire est soumise principalement à deux forces sur les côtés perpendiculaires à

\overset{→}{B}

F=F'=I \:L \:B

(où

L

est la longueur du cylindre) et de moment algébrique total :

ℳ_Δ=2 \,F \:R=2 \,I \:L \:B \:R=I \:S \:B

(où

R

est le rayon du cylindre et

S

l’aire de chaque spire).

◊ remarque : le collecteur est disposé de façon que le sens du courant soit toujours le même par rapport à

\overset{→}{B}

(et non par rapport à la spire).

Action d’un champ uniforme sur un circuit

• Dans un champ magnétique uniforme, la force de Laplace totale est nulle :

$\overset{→}{F}=∫ \left(I \:\overset{→}{d𝓁}×\overset{→}{B} \right) =I .\left(∫ \overset{→}{d𝓁} \right)×\overset{→}{B}=\overset{→}{0}$ .

• Par contre, en notant

\overset{→}{r}=\overset{⟶}{OM}

, le moment des forces exercées est :

$\overset{→}{ℳ}_O=∫ \:\overset{→}{r}×d\overset{→}{F}=I .∫ \left(\overset{→}{r}×(\overset{→}{d𝓁}×\overset{→}{B} \,)\right)$ .

Avec l’identité mathématique :

\overset{→}{U}×(\overset{→}{V}×\overset{→}{W} \,)=(\overset{→}{U}⋅\overset{→}{W} \,) \: \overset{→}{V}-(\overset{→}{U}⋅\overset{→}{V} \,) \: \overset{→}{W}

, on peut écrire :

\overset{→}{ℳ}_O=I .∫ \left(\overset{→}{r}×(\overset{→}{dr}×\overset{→}{B} \, )\right) =I \:∫(\overset{→}{r}⋅\overset{→}{B} \,) \: d\overset{→}{r}-I \:\overset{→}{B} \: ∫ \,\overset{→}{r}⋅ d\overset{→}{r}

.
Mais par ailleurs :

∫ \:\overset{→}{r}⋅ d\overset{→}{r}=\frac{1}{2} \,∫ \:d(r^2 ) =0

sur un parcours fermé ; de façon analogue :

∫ \:d\left((\overset{→}{r}⋅\overset{→}{B} \,) \: \overset{→}{r} \right) =\overset{→}{0}

donc

∫ \:\left(\overset{→}{r}⋅\overset{→}{B}\, \right) \: d\overset{→}{r}=-∫ \:\overset{→}{r}⋅\left(\overset{→}{B}⋅ d\overset{→}{r} \right)

d’où on déduit :

\overset{→}{ℳ}_O=I \:\:∫ \left(\overset{→}{r}⋅\overset{→}{B} \,\right) \: d\overset{→}{r}=\frac{1}{2} I. \left[∫ \:\left(\overset{→}{r}⋅\overset{→}{B} \,\right) \: d\overset{→}{r}-∫ \:\overset{→}{r}⋅\left(\overset{→}{B}⋅ d\overset{→}{r} \right)\right]

puis à l’aide de l’identité vectorielle précédente :

\overset{→}{ℳ}_O=\frac{1}{2} I \:\: ∫ \,\left(\overset{→}{B}×(d\overset{→}{r}×\overset{→}{r} \,)\right)

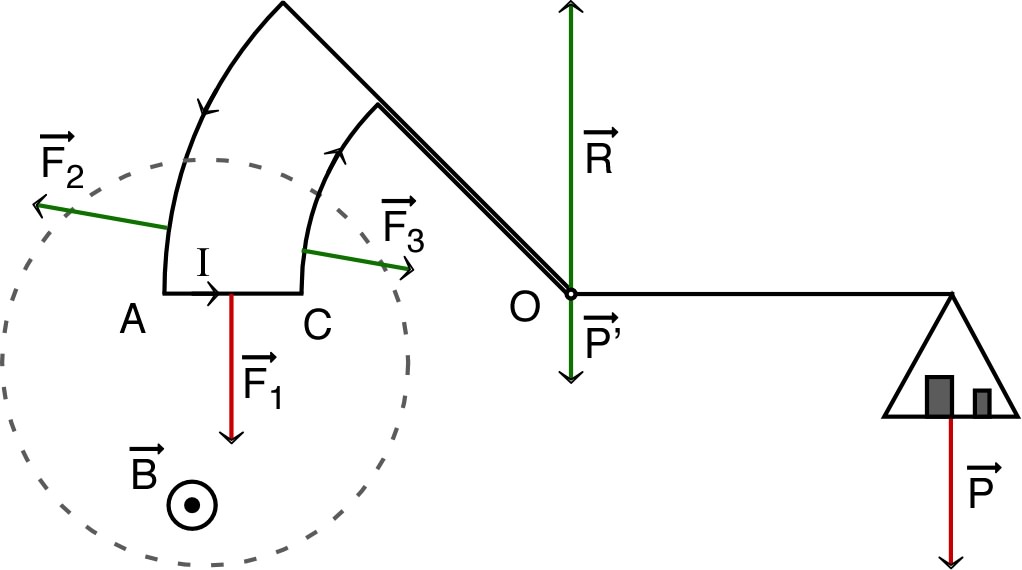
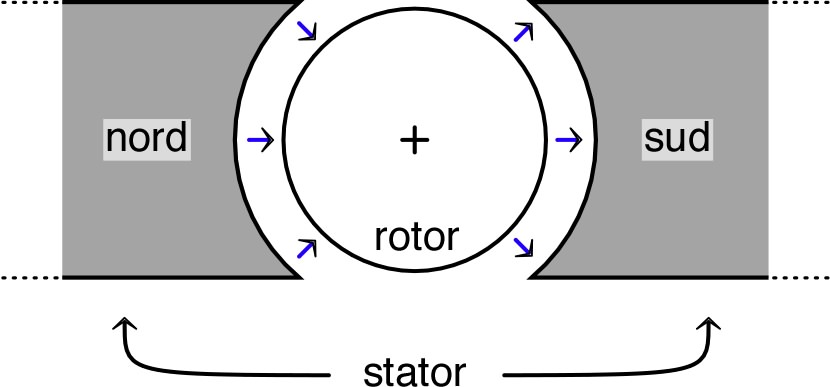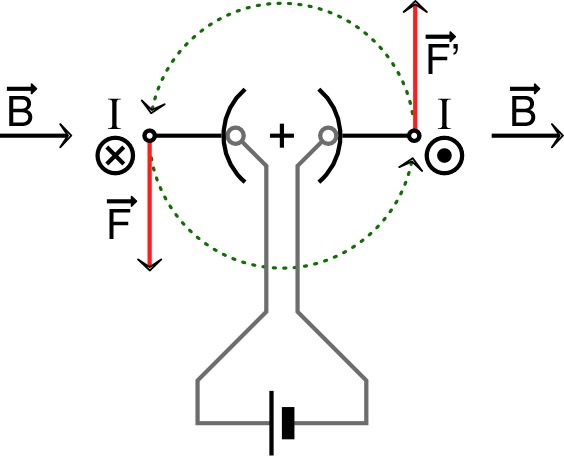Enfin, en fonction du moment dipolaire :

\overset{→}{𝓂}=I \:\overset{→}{S}=\frac{1}{2}\,I \:\: ∫ (\overset{→}{r}×d\overset{→}{r} \, )

, on aboutit à :

\overset{→}{ℳ}_O=\overset{→}{𝓂}×\overset{→}{B}

(analogue au cas du dipôle électrostatique :

\overset{→}{ℳ}_O=\overset{→}{p}×\overset{→}{E}

Ainsi, la principale action d’un champ

\overset{→}{B}

“extérieur” est la tendance à l’orientation de

\overset{→}{𝓂}

selon le champ extérieur

\overset{→}{B}

.

On peut de même associer un moment dipolaire à un barreau aimanté, qui subit donc le même effet.

◊ remarque : pour le calcul du moment des forces, le point de référence

O

est quelconque car la force totale est nulle :

\overset{→}{ℳ}_{O'}=\overset{⟶}{O'O}×\overset{→}{F}+\overset{→}{ℳ}_O=\overset{→}{ℳ}_O

.

• Par analogie avec le dipôle électrostatique, les forces magnétiques dérivent dans ce cas d’une énergie potentielle :

ℰ_p=-\overset{→}{𝓂}⋅\overset{→}{B}

; l’action du moment des forces tend à minimiser

ℰ_p

.

• D’une façon analogue, si le circuit est déformable, les forces de Laplace agissent dans le sens qui tend à augmenter

\overset{→}{𝓂}

en augmentant sa surface s’il est orienté selon

\overset{→}{B}

(et inversement) ; ceci revient également à minimiser

ℰ_p

.

◊ remarque : on peut en outre montrer que l’action secondaire d’un champ extérieur non uniforme est une force totale qui tend à entraîner le circuit vers les champs forts si

\overset{→}{𝓂}

est orienté selon

\overset{→}{B}

(et inversement) ; ceci revient encore à minimiser

ℰ_p

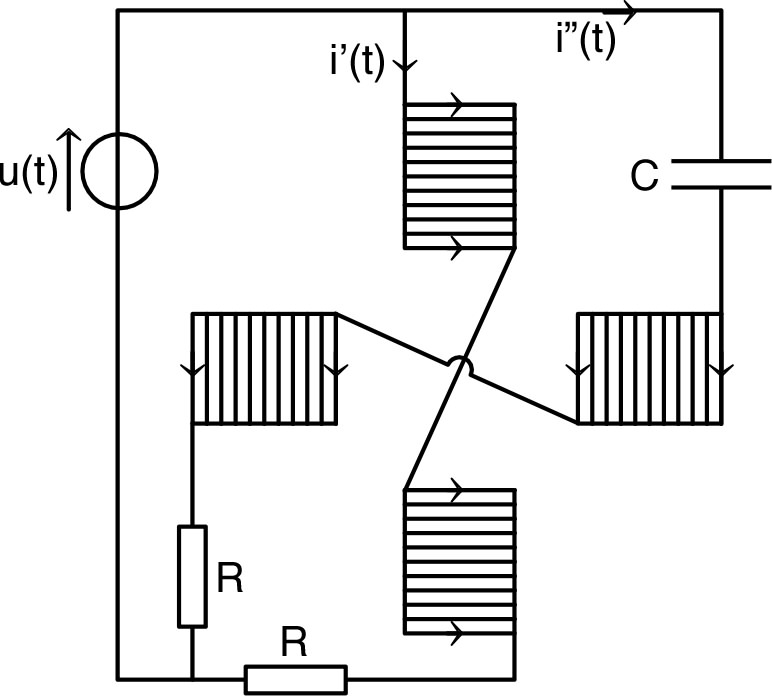
• Compte tenu du fait que :

ℰ_p=-\overset{→}{𝓂}⋅\overset{→}{B}=-I \:\overset{→}{S}⋅\overset{→}{B}=-I \:Φ

(où

Φ

est le flux du champ extérieur uniforme) tend à être minimum, on peut aussi énoncer les propriétés précédentes sous la forme d’une “règle du flux maximum”.

◊ remarque : ces raisonnements considèrent

\overset{→}{B}

constant (magnétostatique) et également

I

constant ; la généralisation nécessiterait de préciser l’énergie potentielle d’interaction du circuit avec le champ extérieur (émission d’ondes électromagnétiques) et de prendre en compte éventuellement l’énergie du circuit dans son propre champ (

ℰ_{magn}=\frac{1}{2} L \:I^2

).

◊ remarque : précédemment, l'unité de courant électrique se déduisait de la loi de force magnétique entre deux circuits (parcourus par le même courant) ; depuis mai 2019, elle découle de celles de temps et de charge, cette dernière se déduisant de la charge élémentaire

\left|q_e \right|=1\text{,}602176634.{10}^{-19} \: \mathrm{C}

, valeur considérée comme exacte (précision relative

{10}^{-14}

).

📖 exercices n° II, III, IV et V.

Action d’un champ tournant sur un aimant

• Puisqu'un électroaimant a des propriétés analogues à celles d'un barreau aimanté, on peut aussi associer un moment dipolaire à un aimant permanent.

• Puisque le moment magnétique tend à s'aligner avec le champ

\overset{→}{B}

, on peut entraîner un aimant en rotation en le soumettant à un champ magnétique tournant. Un tel champ peut être créé à l'aide de plusieurs paires de bobines, parcourues par des courants sinusoïdaux correctement déphasés.

Pour générateur de pulsation

ω

, avec deux paires de bobines, on impose :

$\displaystyle \underline{i}'(t)=I_m \: \mathrm{e}^{\mathrm{j}(ωt+φ')} =\frac{\underline{u}\:}{\underline{Z}'}$ ;
$\displaystyle \underline{i}''(t)=I_m \: \mathrm{e}^{\mathrm{j}(ωt+φ'')} =\frac{\underline{u}\;}{\underline{Z}''}$ ;

$\displaystyle φ'=-\arctan\left(\frac{L\:ω}{R}\right)=-\frac{π}{4}$ ;
$\displaystyle φ''=-\arctan\left(\frac{L\:ω}{R}-\frac{1}{R\,C\,ω}\right)=\frac{π}{4}$ ;

$\displaystyle B_x (t)=B_m \: \cos\left(ωt+\frac{π}{4}\right)$ ;
$\displaystyle B_y (t)=B_m \: \sin\left(ωt+\frac{π}{4}\right)$ .

• On obtient ainsi un moteur “alternatif” synchrone : le rotor (aimant placé au centre) doit tourner à la fréquence imposée par le générateur. La vitesse de rotation ne peut être modifiée qu'avec un générateur de fréquence réglable.

Un tel moteur nécessite d'être lancé, sinon le rotor subit initialement un champ magnétique variant trop vite : l'effet moyen est nul. Ici encore, il est préférable de disposer d'un générateur de fréquence réglable et d'augmenter progressivement celle-ci.

◊ remarque : en remplaçant l'aimant permanent du rotor par bobine court-circuitée, on obtient un moteur “alternatif” asynchrone ; le courants induit dans cette bobine lui donne un moment magnétique, donc elle est entraînée en rotation, quelle que soit la vitesse de rotation du champ

\overset{→}{B}