FORCES MAGNÉTIQUES - corrigé des exercices

A. EXERCICES DE BASE

Principe d’un ampèremètre “absolu”

1.	• Le champ magnétique à l'intérieur d'un solénoïde est quasi-uniforme, orienté selon l'axe et de norme $B=μ_0 \: n \:I$ ; dans le cas étudié ici : $B=12\text{,}6 \:\mathrm{mT}$ .

• L'élément conducteur “utile” de la balance est horizontal à l'équilibre (par construction) et perpendiculaire à l'axe de la bobine (donc au champ

\overset{→}{B}

) ; il subit alors une force verticale (vers le haut ou vers le bas) de norme

F=I \:∆𝓁 \:B=2\text{,}51 \:\mathrm{mN}

.
• À l'équilibre, le moment de cette force est compensé par celui du poids des masses placées sur le plateau de la balance. Si toutefois la balance n'est pas exactement équilibrée “à vide” (sans courant ni masse), alors il peut y avoir un décalage :

ℳ\left(\overset{→}{F} \,\right)+ℳ\left(\overset{→}{P} \,\right)+ℳ_{déc}=0

.
• En inversant le sens du courant, on inverse le sens de

\overset{→}{F}

et celui de son moment. Le nouvel équilibre donne :

ℳ\left(-\overset{→}{F} \,\right)+ℳ\left(\overset{→}{P}' \,\right)+ℳ_{déc}=0

; on en déduit par différence :

2 \:ℳ\left(\overset{→}{F} \,\right)=ℳ\left(\overset{→}{P}'\,\right)-ℳ\left(\overset{→}{P} \,\right)

.
• Faute d'indication dans l'énoncé, on doit supposer que les bras du fléau de la balance sont égaux ; la compensation correspond à l'égalité des normes :

2 \,F=Δm \:\:g

.
• La surcharge nécessaire est donc :

\displaystyle ∆m=\frac{2 \,I \:∆𝓁 \;B}{g}

.
◊ remarque : l'énoncé dit qu'il s'agit d'une surcharge ; mais le signe de la variation

∆m

dépend du sens de

\overset{→}{F}

dans le premier équilibre ; on suppose donc que le sens choisi est celui qui correspond.
• L'application numérique donne :

∆m=512 \:\mathrm{mg}

• L'énoncé indique que l'équilibre est ensuite rétabli en ajoutant une surcharge ; ceci suppose que dans le sens inverse

P'>P

, donc initialement

ℳ\left(\overset{→}{F} \,\right)

ℳ\left(\overset{→}{P} \,\right)

sont de même signe, donc le décalage est ici nécessaire (et doit être assez grand) pour que l'expérience soit possible.
• Avec une balance “normale” (décalage souvent non nul mais faible), on pourrait compenser en modifiant le courant, mais non changer son signe.
• Inversement, lorsque cela est possible, l'avantage de ne changer que le sens est de ne faire intervenir, en valeur absolue, qu'une seule intensité

I

du courant ; ceci permet de mesurer ce dernier par comparaison avec des masses connues. Un tel ampèremètre est “absolu” en ce sens qu'il ne nécessite pas de comparaison entre le courant étudié et des “courants de référence” : c'est le même courant qui est utilisé pour créer le champ magnétique qui cause la force.

Action d’un champ magnétique uniforme sur un cadre

• Le moment vectoriel peut s'écrire

\overset{→}{Γ}=\overset{→}{𝓂} × \overset{→}{B}

avec un moment magnétique

\overset{→}{𝓂}=N \:I \:\overset{→}{S}

; cela donne algébriquement :

Γ=N \:I \:S \:B \; \sin(θ)

avec

S=2 \,a \:h

.
• Dans ce cas (champ magnétique et circuit “constants”), on peut aussi raisonner avec l'énergie potentielle :

ℰ_p=-\overset{→}{𝓂}⋅\overset{→}{B}=-N \:I \:S \:B \; \cos(θ)

; le moment algébrique est ainsi :

\displaystyle Γ=\frac{dℰ_p}{dθ}=N \:I \:S \:B \; \sin(θ)

• Une “aiguille” de boussole s'oriente selon la composante horizontale du champ magnétique terrestre. Un cadre tournant selon un axe vertical peut en principe faire de même, mais il reste à tester si les ordres de grandeur sont raisonnables.
• Avec

N=100

tours de fil ;

a=2 \:\mathrm{cm}

;

h=5 \:\mathrm{cm}

;

I=1 \:\mathrm{A}

(un courant important nécessite un fil plus gros pour éviter l'échauffement...) ; on obtient un moment magnétique

𝓂=N \:I \:S≈0\text{,}2 \:\mathrm{A.m^2}

comparable à celui d'une aiguille de boussole.
• La difficulté technique tient au fait que dans le champ terrestre

N \:I \:S \:B≈4.{10}^{-6} \: \mathrm{N.m}

; un moment de forces aussi faible doit être associé à une suspension très délicate du circuit, d'autant plus “encombrant” qu'il comporte forcément des fils d'alimentation.

Mesures relatives de champs magnétiques

• Puisque l'axe de rotation de l'aiguille de la boussole est vertical et que le moment magnétique

\overset{→}{𝓂}

est horizontal, seule la composante horizontale de

\overset{→}{B}

contribue au moment algébrique selon l'axe vertical.
• En plus des forces magnétiques, l'aiguille est soumise à son poids et à la réaction de l'axe, mais ces forces ont un moment nul par rapport à l'axe.
• En notant

J

le moment d'inertie de l'aiguille, le théorème du moment cinétique peut donc s'écrire sous la forme :

J \:\ddot{θ}+𝓂 \:B \; \sin(θ)=0

.
• Pour les petites oscillations, cela correspond à un oscillateur harmonique de période

\displaystyle T=2π \:\sqrt{\frac{J}{𝓂 \:B}}

. On peut ainsi en déduire :

\displaystyle \frac{B_2}{B_1} =\left(\frac{T_1}{T_2} \right)^2

Composante horizontale du champ magnétique terrestre

• L'élément conducteur “utile” de la balance est horizontal à l'équilibre (par construction) et perpendiculaire à l'axe de la bobine (donc au champ

\overset{→}{B}

) ; il subit donc alors une force verticale (vers le haut ou vers le bas) de norme

F=I \:𝓁 \:B

.
• À l'équilibre, le moment de cette force est compensé par celui du poids des masses placées sur le plateau de la balance :

ℳ\left(\overset{→}{F} \,\right)+ℳ\left(\overset{→}{P} \,\right)=0

.
• En inversant le sens du courant, on inverse le sens de

\overset{→}{F}

et celui de son moment. Le nouvel équilibre donne :

ℳ\left(-\overset{→}{F}\, \right)+ℳ\left(\overset{→}{P}'\,\right)=0

; on en déduit par différence :

2 \,ℳ\left(\overset{→}{F} \,\right)=ℳ\left(\overset{→}{P}'\,\right)-ℳ\left(\overset{→}{P} \,\right)

.
• Puisque les bras du fléau de la balance sont égaux ; la compensation correspond à l'égalité des normes :

2 \,F=2 \,I \:𝓁 \:B=∆m \:\:g

. On obtient ainsi :

\displaystyle B=\frac{∆m \:\:g}{2 \,I \:𝓁}≈2\text{,}5 \:\mathrm{mT}

• En notant

J

le moment d'inertie de l'aimant, le théorème du moment cinétique peut s'écrire sous la forme :

J \:\ddot{θ}+𝓂 \:B \; \sin(θ)=0

.
• Pour les petites oscillations, cela correspond à un oscillateur harmonique de période

\displaystyle T=2π \:\sqrt{\frac{J}{𝓂 \:B}}

. On peut ainsi en déduire :

\displaystyle B_0=B .\left(\frac{T}{T_0} \right)^2≈2.{10}^{-5} \: \mathrm{T}

Roue de Barlow

• Le moment subi par un élément infinitésimal

\overset{→}{d𝓁}

est :

d\overset{→}{ℳ}=\overset{\longrightarrow}{OM} × d\overset{→}{F}

avec

d\overset{→}{F}=I \:\overset{→}{d𝓁} × \overset{→}{B}

.
• En coordonnées cylindriques, avec une direction axiale selon l'axe de la roue :

$\overset{→}{B}=B \;\overset{→}{u}_z$ ; $\overset{→}{d𝓁}=dr \:\overset{→}{u}_r+r \:dθ \:\overset{→}{u}_θ$ ; $d\overset{→}{F}=I \:B .[-dr \:\overset{→}{u}_θ+r \:dθ \:\overset{→}{u}_r ]$ ;
$\overset{\longrightarrow}{OM}=r \:\overset{→}{u}_r$ ; $d\overset{→}{ℳ}=-I \:B \:r \:dr \:\overset{→}{u}_z$ .

• Au total :

\displaystyle \overset{→}{ℳ}=∫_O^A d\overset{→}{ℳ}(M)=-\frac{1}{2} \, I \:B \:R^2 \:\:\overset{→}{u}_z

.
• Le résultat ne dépend pas du trajet du courant car les projections selon

\overset{→}{u}_θ

du mouvement des charges contribuent selon

\overset{→}{u}_r

aux forces de Laplace ; ces contributions ont un moment nul.

B. EXERCICES D'APPROFONDISSEMENT

Principe de l’ampèremètre absolu de Kelvin

• Selon la loi de Biot et Savart

\displaystyle d\overset{→}{B}=\frac{μ_0}{4π} \, \frac{I \:\overset{→}{d𝓁} × \overset{→}{u}_r}{r^2}

et les symétries imposent

\overset{→}{B}=B_x \: \overset{→}{u}_x

.
• Ainsi :

\displaystyle dB_x=\frac{μ_0 \: I \:d𝓁}{4π \:r^2} \: \cos(α)

;

d𝓁=R \:dθ

;

r^2=R^2+x^2

;

\displaystyle \cos(α)=\frac{R}{r}

;

\displaystyle B=B_x=\frac{μ_0 \: N_1 \: I \:R_1^{\:2}}{2 \:\left(R_1^{\:2}+x^2 \right)^{3/2}}

• Le flux à travers la surface latérale est

dΦ=B_r \: 2π \:r \:dx

.
• Par symétrie, hors de l'axe

B_x (r)

passe par un extremum pour

r=0

; on peut donc supposer qu'il varie peu au voisinage de l'axe. Le flux à travers les bases est alors :

Φ≈[B_x (x+dx)-B_x (x)] \:\: π \:r^2

.
• Le flux à travers le cylindre étant nul :

B_r \: 2π \:r \:dx+ dB_x \: π \:r^2=0

;

\displaystyle B_r≈-\frac{r}{2} \, \frac{dB_x}{dx}

.
• Ceci donne :

\displaystyle B_r≈\frac{3 \,μ_0 \: N_1 \: I \:R_1^{\:2} \; r \:x}{4 \:\left(R_1^{\:2}+x^2 \right)^{5/2}}=\frac{3}{2} \, \frac{r \:x}{R_1^{\:2}+x^2} \: B_x

“justifiant” ainsi qu'au voisinage de l'axe (

r≪R_1

) le champ reste assez bien axial, cela d'autant mieux qu'on ne s'éloigne pas trop du centre de la bobine (

x≪R_1

• Les moments magnétiques étant initialement alignés, ils le restent. La composante

B_x

du champ de

b_1

cause sur

b_2

des forces radiales dont la somme est nulle par symétrie.
• Par contre la composante radiale

B_r

cause sur

b_2

une force de Laplace axiale (

b_1

subit l'action réciproque) de norme :

\displaystyle F=∫ \:I \:B_r \: R_2 \: dθ≈\frac{3π}{2} \: μ_0 \: N_1 \: N_2 \: I^2 \, \frac{R_1^{\:2} \: R_2 \: x}{\left(R_1^{\:2}+x^2 \right)^{5/2}}

.
• Pour un courant orienté comme

\overset{→}{u}_θ

B_r

selon

\overset{→}{u}_r

, cette force est orientée selon

\overset{→}{u}_θ × \overset{→}{u}_r=-\overset{→}{u}_x

(les bobines parcourues par des courants de même sens s'attirent).

4.a.	• L'extremum correspond à l'annulation de la dérivée : $\displaystyle \frac{d}{dx} \left(\frac{x}{\left(R_1^{\:2}+x^2 \right)^{5/2}} \right)=\frac{R_1^{\:2}-4 \:x^2}{\left(R_1^{\:2}+x^2 \right)^{7/2}} =0$ ; $\displaystyle x=\frac{R_1}{2}$ . ◊ remarque : ceci ne respecte que très médiocrement la condition supposée $x≪R_1$ . • Cela correspond à : $\displaystyle F_M≈\frac{24π}{25 \:\sqrt{5}} \, μ_0 \: N_1 \: N_2 \: I^2 \: \frac{R_2}{R_1^{\:2}}$ .

4.b.	• On obtient numériquement : $F_M≈0\text{,}27 \:\mathrm{N}$ .

5.a.	• Pour obtenir un moment maximum il faut que les quatre bobines agissent dans le même sens. • Supposons que le sens du courant dans $c_1$ lui donne un champ orienté vers le haut, alors la disposition correspond à l'équivalent de $x>0$ pour $b_2$ et lui imposerait un effet vers le bas (maximum) pour un courant dans le même sens. L'obtention d'un effet vers le haut impose donc pour $b_2$ un courant de sens inverse. • Pour que la disposition corresponde à $x>0$ pour $b_2$ par rapport à $d_1$ il faut que cette dernière ait un courant de même sens, d'où une action vers le haut. Cela impose donc pour $d_1$ un courant de sens inverse à $c_1$ . ◊ remarque : pour un même sens du courant, la disposition relative de $c_1$ et $d_1$ correspondrait aux bobines de Helmholtz, pour lesquelles $B_x$ dépend le moins possible de $x$ , donc avec $B_r$ très faible (hors de propos ici). 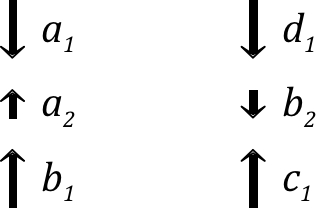• Il suffit alors d'imposer une configuration analogue à gauche avec le sens contraire pour la bobine $a_2$ afin qu'elle subisse une action vers le bas.

5.b.	• En supposant que le poids agit selon l'axe des bobines, le nouvel équilibre impose : $∆m \:\:g=4 \,F_M$ . • Cela donne : $\displaystyle ∆m=\frac{4 \,F_M}{g}≈110 \:\mathrm{g}$ . • Un tel dispositif permet une mesure “absolue” car toutes les bobines sont parcourues par le même courant mesuré (on ne procède pas par comparaison). On prend en outre la précaution de procéder par différence de deux équilibres : l'effet du courant est associé à la modification de l'équilibre.