FORCES MAGNÉTIQUES

FORCES MAGNÉTIQUES - exercices

A. EXERCICES DE BASE

Principe d’un ampèremètre “absolu”

1. • Un solénoïde, dont la longueur est très grande par rapport au rayon, comporte

n=1000 \:\mathrm{m^{-1}}

tours de fil (par mètre). Calculer le champ magnétique au centre de ce solénoïde, lorsqu'il est parcouru par un courant

I=10\text{,}0 \:\mathrm{A}

.

2. • Une fente (assez étroite pour ne pas perturber le champ magnétique) permet d’introduire dans ce solénoïde l’extrémité du bras d’une balance de Cotton, dont l’élément conducteur “utile” (perpendiculaire à l’axe du solénoïde) a pour longueur

∆𝓁=2\text{,}0 \:\mathrm{cm}

.
• Le même courant

I

parcourt le solénoïde et la balance de Cotton mais, grâce à un inverseur, on peut inverser le sens de ce courant dans l’élément conducteur de la balance sans le modifier dans le solénoïde. L’équilibre étant réalisé pour un sens du passage du courant, on actionne l’inverseur ; calculer (en fonction de

I

) la surcharge

Δm

qu’on doit placer sur le plateau de la balance pour rétablir l’équilibre (en supposant que les deux bras de fléau sont de même longueur).

Donnée :

g=9\text{,}81 \:\mathrm{m.s^{-2}}

.

3. • Quel est l’intérêt du dispositif avec inverseur par rapport à un dispositif à mesure simple ?

Action d’un champ magnétique uniforme sur un cadre

• On enroule

N

tours de fil sur un cadre rectangulaire de hauteur

h

et de largeur

2 \,a

, mobile autour d’un axe vertical

Δ

passant par les milieux des “largeurs”. Ce cadre, parcouru par un courant

I

, est plongé dans un champ magnétique

\overset{→}{B}

uniforme horizontal. La normale au cadre (orientée d’après le sens de

I

) fait un angle

θ

avec

\overset{→}{B}

.

1. • Calculer le moment algébrique

Γ

(par rapport à l’axe

Δ

) des forces magnétiques qui s’exercent sur le cadre. Peut-on retrouver ceci directement par une autre méthode ?

2. • Ce dispositif peut-il constituer pratiquement une boussole ?

Donnée : composante horizontale du champ magnétique terrestre :

B_0=2.{10}^{-5} \: \mathrm{T}

Mesures relatives de champs magnétiques

• On montre expérimentalement qu’un petit aimant permanent, plongé dans un champ magnétique uniforme

\overset{→}{B}

, subit un ensemble de forces de moment

\overset{→}{Γ}=\overset{→}{𝓂} × \overset{→}{B}

, où

\overset{→}{𝓂}

est un vecteur (caractéristique des propriétés magnétiques de l’aimant) dont la grandeur et l’orientation (par rapport à l’aimant) sont constantes (dans les conditions considérées ici). Par exemple pour une aiguille de boussole,

\overset{→}{𝓂}

a la direction et le sens de l’aiguille.
• Montrer que la mesure des périodes d’oscillation

T_1

T_2

d’une aiguille de petite boussole autour de sa position d’équilibre, en deux points où les champs magnétiques ont respectivement pour composantes horizontales

B_1

B_2

(en norme), permet de déterminer approximativement le rapport

\displaystyle \frac{B_2}{B_1}

Composante horizontale du champ magnétique terrestre

• L’étude expérimentale du champ magnétique créé par un solénoïde “infini”, parcouru par un courant

I_0

, montre que le champ magnétique est uniforme à l’intérieur du solénoïde et qu’il est nul à l’extérieur.

1. • Une fente étroite pratiquée dans ce solénoïde (horizontal) permet d’y introduire le bras d’une balance de Cotton sans en modifier le champ magnétique. L’élément “utile” de la balance est horizontal et perpendiculaire au champ magnétique ; il a une longueur

𝓁=2 \:\mathrm{cm}

et est parcouru par un courant

I=10 \:\mathrm{A}

.
• La balance (dont les deux bras sont égaux) est initialement équilibrée. En inversant alors le sens du courant, on constate qu’il faut ajouter une surcharge

∆m=0\text{,}10 \:\mathrm{g}

pour rétablir l’équilibre. Quelle est la norme du champ magnétique à l’intérieur du solénoïde ?

2. • Un petit aimant allongé, suspendu en son milieu à un fil vertical sans raideur en torsion, est placé à l’intérieur du solénoïde ; il oscille alors autour de sa position d’équilibre avec une période

T=0\text{,}45 \:\mathrm{s}

. Placé hors du solénoïde (donc soumis uniquement au champ magnétique terrestre), sa période d’oscillation est

T_0=5 \:\mathrm{s}

. En déduire la valeur de la composante horizontale du champ magnétique terrestre.

Roue de Barlow

• Une “roue de Barlow” de centre

O

est constituée d'un disque métallique mobile dans un plan vertical. La partie inférieure est en contact (au point

A

) avec un liquide conducteur du courant.
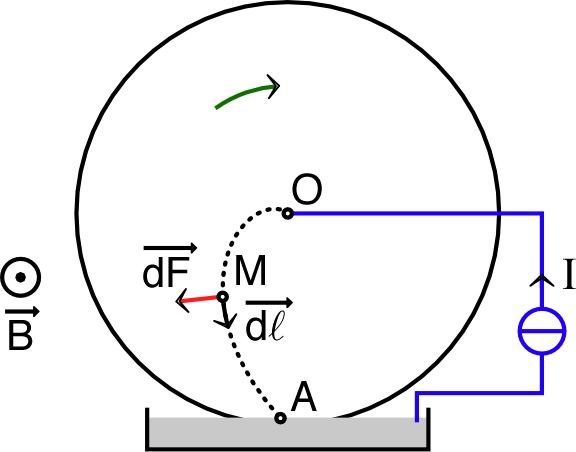
• L'ensemble est placé dans une zone où existe un champ magnétique

\overset{→}{B}

(horizontal) perpendiculaire au plan de la roue.
• Un générateur, relié à l'axe et à la cuve contenant le liquide, impose dans la roue un courant

I

entre

O

A

, mais on ne connaît pas le trajet exact suivi par le courant.

• En raisonnant sur un trajet quelconque du courant (allant de

O

A

), exprimer le moment total des forces de Laplace subies par la roue.
• Expliquer pourquoi le résultat ne dépend pas du trajet suivi par le courant.

B. EXERCICES D'APPROFONDISSEMENT

Principe de l’ampèremètre absolu de Kelvin

• Une bobine circulaire plate

b_1

comporte

N_1

spires, de centre

O

et de rayon moyen

R_1

; elle est parcourue par un courant

I

.

1. • Calculer le champ magnétique algébrique

B(x)

à l’abscisse

x

sur l’axe

Ox

de la bobine.

2. • En exprimant que le flux de

\overset{→}{B}

sortant d’une surface fermée est nul, puis en l’appliquant à un petit cylindre d’axe

Ox

, de rayon

r

et de hauteur infinitésimale

dx

, montrer que le champ magnétique a, au voisinage de l’axe, une composante radiale

\displaystyle B_r=-\frac{r}{2} \: \frac{∂B(x)}{∂x}

3. • Une seconde bobine circulaire plate

b_2

comporte

N_2

spires de rayon moyen

R_2≪R_1

; elle est parcourue par le même courant

I

que

b_1

. Elle est disposée de façon que les axes de

b_1

b_2

coïncident ; son centre est à l’abscisse

x

par rapport à

b_1

. Déterminer la force

F(x)

qui s’exerce entre ces bobines.

4. a) Pour quelle distance

F(x)

a-t-elle sa valeur maximale

F_M

? Déterminer l’expression de

F_M

.
b) Effectuer l’application numérique pour :

$R_1=20 \:\mathrm{cm}$ ; $N_1=800$ ; $R_2=2 \:\mathrm{cm}$ ; $N_2=100$ ; $I=2 \:\mathrm{A}$ .

5. • Pour mesurer un courant de façon “absolue”, on réalise le dispositif suivant :

• Les bobines

a_1

b_1

c_1

d_1

sont semblables à

b_1

, respectivement coaxiales deux à deux ; la distance de deux d’entre elles situées d’un même côté est égale à leur rayon commun.
• Les bobines

a_2

b_2

sont semblables à

b_2

, suspendues aux deux extrémités du fléau d’une balance de précision, de façon qu'elles aient respectivement le même axe que les grandes bobines situées du même côté. Dans la position d’équilibre, les petites bobines sont (de chaque côté) à mi-distance entre les grandes.
• Toutes les bobines sont parcourues par le même courant

I

; la balance est équilibrée pour

I=0

.

a) Préciser sur un schéma le sens des courants à respecter pour que le moment du couple de forces tendant à faire basculer dans le sens de la descente du plateau de gauche soit maximal.
b) On fait passer un courant

I=2 \:\mathrm{A}

; calculer la surcharge

∆m

à ajouter sur le plateau de droite pour rétablir l’équilibre. Montrer que ce dispositif permet une mesure “absolue” du courant.

Donnée :

g=9\text{,}81 \:\mathrm{m.s^{-2}}