ÉM. IV - FORCES ÉLECTROMAGNÉTIQUES


Notion de champ magnétique

• On constate à l'état naturel l'existence de matériaux pourvus d'une “aimantation” dite “magnétique” ; cela peut être reproduit expérimentalement (et utilisé par exemple pour l'orientation d'une aiguille de boussole).

Lorentz_Im/Magnet0873.png

Ces phénomènes ne sont pas indépendants des effets électriques (décrits à l'aide d'un vecteur champ électrique E→\overset{→}{E} ) : des circuits parcourus par un courant peuvent présenter des propriétés magnétiques similaires (de façon générale, l'ensemble de ces effets est nommé “électromagnétisme”).

Cela peut être décrit à l'aide d'un vecteur “champ magnétique” B→\overset{→}{B} ; l'étude en sera précisée dans les chapitres suivants.

◊ remarque : l'unité de base du champ magnétique est le tesla\mathrm{tesla} (symbole T\mathrm{T} ), mais les champs usuels sont plutôt de l'ordre du millitesla\mathrm{millitesla} .

Force électromagnétique de Lorentz

• Placée dans un champ électrique E→\overset{→}{E} et un champ magnétique B→\overset{→}{B} , une particule de charge électrique qq et de vitesse v→\overset{→}{v} est soumise à une force électromagnétique (force de Lorentz) :  F→=q.(E→+v→×B→)\overset{→}{F}=q.\left(\, \overset{→}{E} + \overset{→}{v} × \overset{→}{B} \,\right) .

☞ remarque : d'une façon générale la force magnétique  F→m=qv→×B→\overset{→}{F}_m=q \:\overset{→}{v} × \overset{→}{B}  est perpendiculaire au déplacement, donc elle ne travaille pas.

◊ remarque : dans un conducteur (globalement neutre) parcouru par un courant, les forces électriques sur les charges des deux signes se compensent, mais les forces magnétiques ne se compensent généralement pas ; leur résultante correspond à une force macroscopique (force de Laplace), subie par le conducteur, qui est à la base du fonctionnement de nombreux dispositifs électromécaniques.

Particules chargées dans un champ électrostatique uniforme

• Une particule de charge qq et de masse mm (mais de poids comparativement négligeable), soumise à un champ électrostatique E→\overset{→}{E} uniforme, subit une force  F→=ma→=qE→\overset{→}{F}=m \:\overset{→}{a}=q \:\overset{→}{E}  constante : son mouvement est uniformément accéléré.

Particules chargées dans un champ magnétostatique uniforme

• Soit une particule de charge  q<0q<0  et de masse mm (mais de poids négligeable), soumise à un champ magnétique B→\overset{→}{B} uniforme et constant, selon l'axe OzOz , avec initialement :  (x ; y ; z)=(x0 ; 0 ; 0)(x\text{ ; }y\text{ ; }z)=(x_0\text{ ; }0\text{ ; }0) ,  x˙=0\dot{x}=0 ,  y˙=v0y>0\dot{y}=v_{0y}>0  et  z˙=v0z\dot{z}=v_{0z} .

La force de Lorentz peut s’écrire :  F→=qv→×B→=qB.[y˙u→x−x˙u→y]\overset{→}{F}=q \:\overset{→}{v} × \overset{→}{B}=q \:B.\left[\dot{y} \: \overset{→}{u}_x-\dot{x} \:\overset{→}{u}_y \right]  ce qui donne :  mẍ=qBy˙m \:\ddot{x}=q \:B \:\dot{y}  ;  mÿ=−qBx˙m \:\ddot{y}=-q \:B \:\dot{x}  ;  mz̈=0m \:\ddot{z}=0 .  On en déduit en particulier que vzv_z est constante, donc on n’a plus qu’à étudier la projection sur xOyxOy .

• Le système d’équations différentielles combinées en vxv_x et vyv_y peut se résoudre en intégrant (ou en dérivant) l’une des équations et en reportant le résultat dans l’autre.

Ainsi, compte tenu des conditions initiales :  x˙=qBmy\displaystyle \dot{x}=\frac{q \:B}{m} \: y  ;  donc en reportant :  ÿ+ω2y=0\ddot{y}+ω^2 \: y=0   avec   ω=|q|Bm\displaystyle ω=\frac{\left|q\right| \: B}{m} .

Compte tenu des conditions initiales, on en déduit :  y=Ymsin(ωt) y=Y_m \: \sin(ω \:t) .  Ceci donne :  y˙=ωYmcos(ωt)\dot{y}=ω \:Y_m \: \cos(ω \:t)  et les conditions initiales imposent :  Ym=v0yω\displaystyle Y_m=\frac{v_{0y}}{ω} .

En reportant :  x˙=−v0ysin(ωt)\dot{x}=-v_{0y} \; \sin(ω \:t)  puis, d'après les conditions initiales, on en déduit :  x−x0=v0yω[cos(ωt)−1]\displaystyle x-x_0=\frac{v_{0y}}{ω} \: [\cos(ω \:t)-1] .

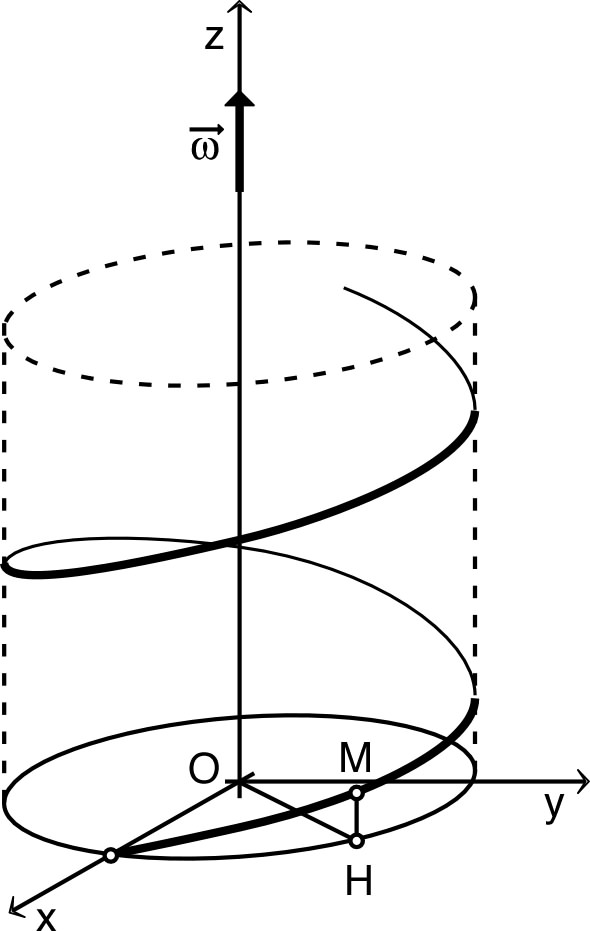
• Ces projections correspondent (selon xOyxOy ) à un mouvement circulaire de rayon  r=v0yω\displaystyle r=\frac{v_{0y}}{ω}  dont le centre a pour coordonnées :  x1=x0−rx_1=x_0-r   et   y1=0y_1=0 .

Ce mouvement projeté est circulaire uniforme ; le mouvement “total” est donc hélicoïdal uniforme, avec une vitesse de norme  v0y2+vz2\sqrt{v_{0y}^{\:2}+v_z^{\:2}}  constante.

◊ remarque : le schéma ci-contre correspond à  x1=0x_1=0 .
Lorentz_Im/Lorentz_Im1.jpg

◊ remarque : on peut résoudre le système des deux premières équations avec la notation complexe  Z=x+iyZ=x+\mathrm{i} \:y  ;  on obtient ainsi :  mZ̈+iqBZ˙=0m \:\ddot{Z}+\mathrm{i} \:q \:B \:\dot{Z}=0  d'où on déduit Z˙\dot{Z} , puis ZZ .

◊ remarque : le système différentiel en vxv_x et vyv_y peut aussi se résoudre sous la forme matricielle :  v→˙=[𝐌]v→\dot{\overset{→}{v}}=\left[\mathbf{M}\right] \: \overset{→}{v}  ;  en diagonalisant la matrice [𝐌]\left[\mathbf{M}\right] on obtient les “vecteurs propres” (complexes)  α=vx+ivyα=v_x+\mathrm{i} \:v_y  et  β=vx−ivyβ=v_x-\mathrm{i} \:v_y  avec les valeurs propres respectives −i-\mathrm{i} et +i+\mathrm{i}  ;  on résout alors avec les variables αα et ββ puis on en déduit  vxv_x  et  vyv_y , puis xx et yy .

Champs électrique et magnétique uniformes

• Tous les cas avec à la fois un champ électrostatique et un champ magnétostatique uniformes conduisent à des systèmes d'équations dont la résolution découle des mêmes méthodes.

◊ remarque : l'étude des aurores boréales et australes correspond à une généralisation pour des champs non uniformes.

◊ remarque : on obtient des équations analogues pour un point matériel soumis à une force de pesanteur uniforme, dans un référentiel tournant autour d'un axe fixe avec une vitesse de rotation constante, où intervient une force d'inertie  f→c=−2mω→×v→′\overset{→}{f}_c=-2 \,m \:\overset{→}{ω} × \overset{→}{v}'  ;  on obtient aussi des équations analogues pour les balles en rotation (lift, slice...) pour lesquelles il faut ajouter une force de Magnus  f→M=λω→×v→\overset{→}{f}_M=λ \:\overset{→}{ω} × \overset{→}{v} .

📖 exercices n° I, II et III.