MESURE DU QUOTIENT e/m POUR LES ÉLECTRONS

MESURE DU QUOTIENT $e/m$ POUR LES ÉLECTRONS - TP

Dispositif expérimental

Champ magnétique

• On crée un champ magnétique quasi-uniforme à l’aide de bobines de Helmholtz : deux bobines coaxiales de même rayon

R'

, séparées par une distance égale à ce rayon.

• On montre en effet que le champ magnétique créé sur l’axe par une bobine placée à l’abscisse

x_0

est parallèle à l’axe et de la forme :

\displaystyle B=\frac{μ_0 \: N \:I}{2 \,R'.\left[1+\frac{(x-x_0 )^2}{{R'}^2} \right]^{3/2}}

.
En déduire le champ total créé par les deux bobines placées aux abscisses

\displaystyle -\frac{R'}{2}

\displaystyle +\frac{R'}{2}

.

• Montrer que les trois premières dérivées de l’expression obtenue sont nulles pour

x=0

; en déduire, par un développement limité à l’ordre

4

, que le champ magnétique sur l’axe est quasi-uniforme dans tout l’intervalle entre les deux bobines (variation maximum de l’ordre de

5 \:%

sur les bords).

• On peut en outre montrer, bien que la démonstration soit nettement plus compliquée, qu’il en est de même pour les variations du champ magnétique dans les directions perpendiculaires à l’axe. On suppose donc que le champ dans la “zone utile” est :

\displaystyle B=\frac{μ_0 \: N \:I}{R'.\,\left(\frac{5}{4}\right)^{3/2}}

avec une incertitude de

3 \:%

.

• Mesurer

R'

(

15\text{,}0

15\text{,}5 \:\mathrm{cm}

selon les montages) et en déduire la relation entre

B

I

pour

N=130

spires et

μ_0=4π \:{10}^{-7} \: \mathrm{H.m^{-1}}

. Le montage est muni d’une alimentation en courant et d’un ampèremètre pour mesurer

I

et en déduire

B

.

• La manipulation nécessite d’utiliser un champ magnétique assez intense si on veut pouvoir négliger les perturbations causées (entre autres) par le champ magnétique terrestre ; mais il faut tout de même ne pas exagérer l’intensité du courant dans les bobines pour ne pas les détériorer ; en pratique, il faut

I≈1\text{,}5 \:\mathrm{A}

. Il faut par ailleurs éviter de laisser des objets en fer à proximité du montage.

◊ remarque : on peut tester si l'orientation du montage (perpendiculaire au champ magnétique terrestre) apporte une amélioration.

Faisceau d’électrons

• On place au centre des bobines une ampoule “à vide” munie d’un canon à électron dont on mesure la tension accélératrice

U

. Calculer la relation entre cette tension et la vitesse des électrons émis.

• La manipulation nécessite d’utiliser une tension accélératrice assez grande si on veut raisonnablement limiter les différentes causes d’incertitudes ; mais il faut ne pas exagérer la tension pour ne pas détériorer le dispositif ; en pratique, il faut

U≈100

\mathbf{300} \:\mathrm{\mathbf{V}}

maximum (ceci implique de bien faire attention lors du montage quand on utilise un générateur qui peut fournir jusqu’à

\mathbf{700} \:\mathrm{\mathbf{V}}

!)..

• Montrer que les électrons ont un mouvement circulaire uniforme s’ils sont lancés avec une vitesse initiale perpendiculaire à l’axe (régler éventuellement la position de l’ampoule “à vide” pour que cette condition soit vérifiée). Calculer la relation entre le champ magnétique, le rayon

R

de la trajectoire, la vitesse

v

des électrons, leur masse et leur charge.

◊ remarque : sur certains montages, il peut être nécessaire de régler l'orientation de l'ampoule pour que la vitesse initiale

\overset{→}{v}_0

soit perpendiculaire au champ magnétique (sinon le mouvement est hélicoïdal).

• L’ampoule “à vide” contient en fait un gaz sous très faible pression, qui donne une trace de luminescence sur le trajet des électrons (par ionisation des atomes). Il faut toutefois procéder dans l’obscurité car le faisceau est très peu lumineux.

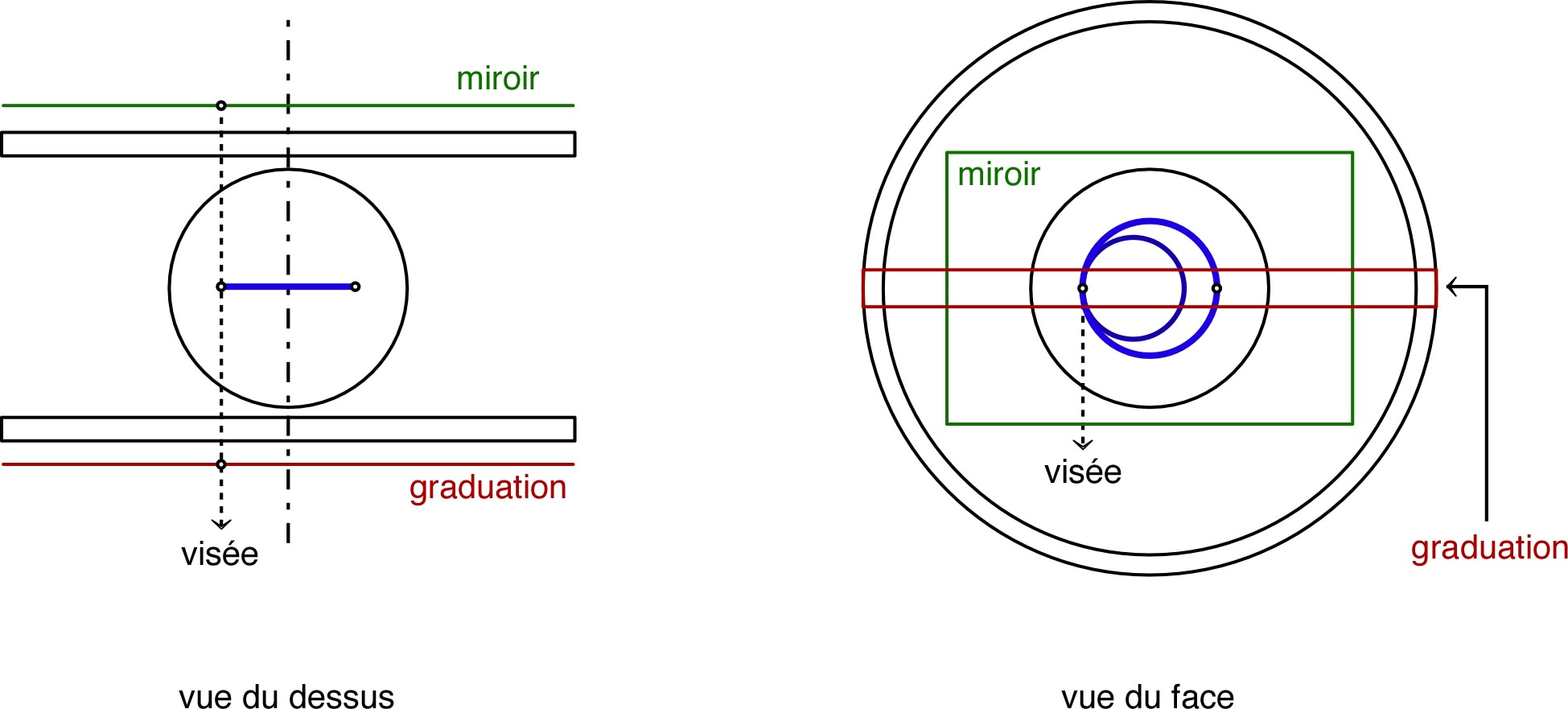
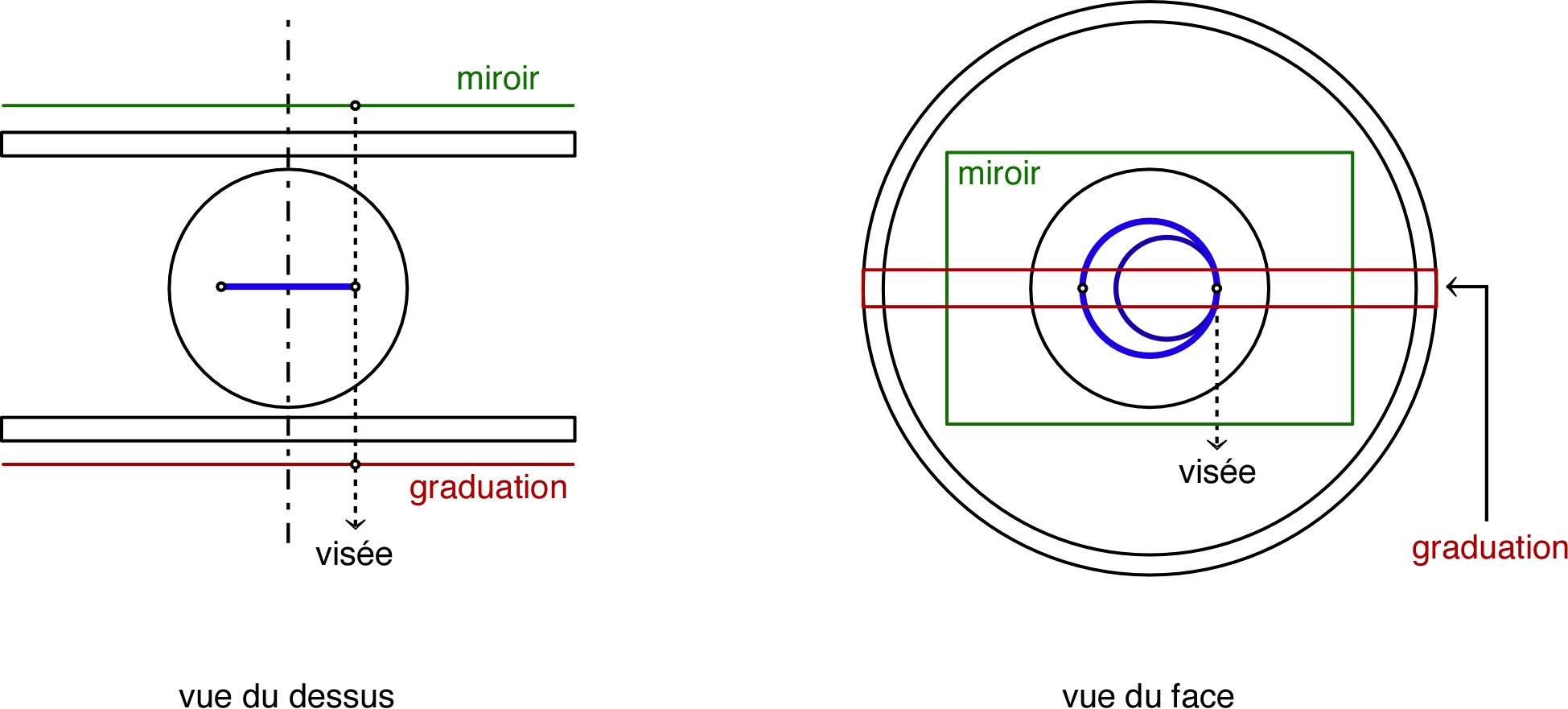
• Le montage est muni d’un miroir qui permet de mesurer le diamètre de la trajectoire circulaire en évitant les erreurs de parallaxe : on place une règle graduée à l’avant et on repère la graduation qui est alignée avec le côté gauche du faisceau et son image dans le miroir (il faut repérer la position dans l’obscurité, puis éclairer pour lire la graduation) :

• On procède ensuite de même pour le côté droit, sans déplacer la règle entre-temps, puis on en déduit le diamètre par différence :

Mesures

Étude en fonction de la tension accélératrice

• Montrer que, pour un champ

B

donné, le carré du diamètre est proportionnel à la tension :

\displaystyle D^2=\frac{8 \,m}{e \:B^2} \: U

.

• Vérifier expérimentalement cette proportionnalité, pour

I=1\text{,}5 \:\mathrm{A}

100 \:\mathrm{V}≤U≤300 \:\mathrm{V}

, puis en déduire le quotient :

\displaystyle \frac{e}{m}=\frac{8 \,U}{D^2 \: B^2}

Étude en fonction du champ magnétique

• Montrer que, pour une tension accélératrice donnée, l’inverse du diamètre est proportionnel au champ magnétique :

\displaystyle \frac{1}{D}=\sqrt{\frac{e}{8 \,m \:U}} \; B

.

• L’étude expérimentale est dans ce cas plus difficile, car on ne peut pas trop diminuer

B

(pour éviter des mesures trop imprécises) et on ne peut pas trop augmenter

B

(pour éviter un échauffement excessif des bobines).

• Régler

I=1\text{,}0 \:\mathrm{A}

, puis augmenter

U

jusqu’à la plus grande valeur possible sans que le faisceau s’approche trop du verre de l’ampoule. Vérifier alors expérimentalement la proportionnalité, pour la valeur de

U

ainsi obtenue et pour

1\text{,}0≤I≤2\text{,}5 \:\mathrm{A}

(en contrôlant fréquemment la température des bobines quand le courant dépasse

1\text{,}5 \:\mathrm{A}

), puis en déduire le quotient :

\displaystyle \frac{e}{m}=\frac{8 \,U}{D^2 \: B^2}