FORCES ÉLECTROMAGNÉTIQUES - corrigé des exercices

A. EXERCICES DE BASE

Fréquence cyclotron

1. Méthode analytique

• La force de Lorentz peut s’écrire :

\overset{→}{F}=q \:\overset{→}{v} × \overset{→}{B}=q \:B.\left[\dot{y} \: \overset{→}{u}_x-\dot{x} \: \overset{→}{u}_y \right]

et la relation fondamentale de la dynamique correspond à :

m \:\ddot{x}=q \:B \:\dot{y}

;

m \:\ddot{y}=-q \:B \:\dot{x}

;

m \:\ddot{z}=0

. On en déduit en particulier que

v_z

est constante, donc on n’a plus qu’à étudier la projection sur

Oxy

.
• Le système d’équations différentielles combinées en

v_x

v_y

peut se résoudre par exemple en intégrant l’une des équations :

\displaystyle \dot{x}=\frac{q \:B}{m} \, y+K

, où la constante d'intégration

K=0

se déduit des conditions initiales

y(0)=0

\dot{x}(0)=0

.
• La substitution dans l'autre équation du résultat obtenu donne :

\ddot{y}+ω^2 \: y=0

avec la “pulsation”

\displaystyle ω=\frac{\left|q\right| \: B}{m}

(qui est en fait ici une vitesse de rotation).
◊ remarque : on peut aussi dériver l’une des équations au lieu d'intégrer, puis substituer de façon analogue, mais c'est généralement plus long.
• On en déduit :

y=Y \; \cos(ω \:t+ϕ)

où la condition initiale

y(0)=0

impose

ϕ=±\frac{π}{2}

c'est-à-dire

y=±Y \; \sin(ω \:t)

. La condition initiale

\dot{y}(0)=±ω \:Y=v_{0y}

impose en outre

\displaystyle Y=\frac{\left|v_{0y} \right|}{ω}

et ainsi :

\displaystyle y=\frac{v_{0y}}{ω} \: \sin(ω \:t)

.
◊ remarque : on choisit généralement

Y>0

en décalant si nécessaire le déphasage de

π

.
• En reportant :

\dot{x}=\mathrm{sgn}(q) \:v_{0y} \; \sin(ω \:t)

; on obtient par intégration :

\displaystyle x=- \mathrm{sgn}(q) \: \frac{v_{0y}}{ω} \: \cos(ω \:t) + K'

, où la constante d'intégration

\displaystyle K'=x_0+\mathrm{sgn}(q) \: \frac{v_{0y}}{ω}

se déduit de la condition initiale

x(0)=x_0

. Finalement :

\displaystyle x=x_0+\mathrm{sgn}(q) \: \frac{v_{0y}}{ω} \: [1-\cos(ω \:t)]

.
◊ remarque : la projection du mouvement sur le plan

Oxy

est donc circulaire uniforme (à “vitesse projetée”

V=\left|v_{0y} \right|

constante) ; la trajectoire est une hélice de pas constant

\displaystyle \frac{2π \:r}{\left|\tan(α)\right|}

, avec

α=\left(\overset{→}{v} \, ;\overset{→}{B} \right)

2. Méthode géométrique

◊ remarque : cette méthode n'est pas tout à fait adaptée au programme de MPSI, qui n'aborde pas la définition du “rayon de courbure” local d'une courbe quelconque ; elle peut toutefois constituer un approfondissement intéressant.
• La force de Lorentz

\overset{→}{F}=q \:\overset{→}{v} × \overset{→}{B}

est perpendiculaire à

\overset{→}{B}

, donc à

\overset{→}{u}_z

; par suite

a_z=0

v_z=v_{0z}

est constante.
• La force

\overset{→}{F}

est aussi perpendiculaire à

\overset{→}{v}

, donc elle ne travaille pas et

v=v_0

est constante. Par suite

\displaystyle \cos(α)=\cos\left(\overset{→}{v} \:;\overset{→}{B} \,\right)=\frac{v_z}{v}

est constant, ainsi :

F=\left|q\right| \: v \:B \:\left|\sin(α) \right|

est aussi constante.
• L’accélération a donc une norme

\displaystyle a=\frac{F}{m}

constante ; or, pour un mouvement dont la vitesse à une norme constante, la norme de l'accélération est liée au rayon de courbure local par la relation

\displaystyle a=\frac{v^2}{R}

, donc le rayon de courbure

R

est lui aussi constant.
• Puisque

α=\left(\overset{→}{v} \: ;\overset{→}{B} \right)

est constant, la projection de la courbe sur

Oxy

a une courbure constante : c’est donc un cercle de rayon

r

tel que

\displaystyle a=\frac{v^2}{R}=\frac{[v \;\sin(α) ]^2}{r}

, c’est-à-dire

\displaystyle r=\frac{v \;\left|\sin(α) \right|}{ω}

• Ce cercle est parcouru par la projection de

M

avec une “vitesse projetée” constante :

v \;\left|\sin(α) \right|

; ce qui correspond à une vitesse angulaire :

\displaystyle ω=\frac{v \;\left|\sin(α) \right|}{r}=\frac{\left|q\right| \: B}{m}

. La rotation se fait autour de la direction de

\overset{→}{B}

avec le sens qui a le signe de

-q

; la trajectoire est une hélice de pas constant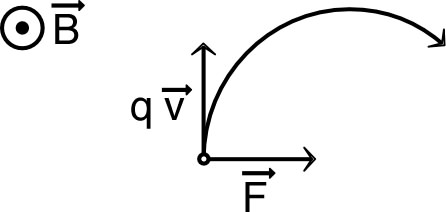

\displaystyle \frac{2π \:r}{\left|\tan(α)\right|}

• Soient donc

x_1

y_1

les coordonnées du centre du cercle projeté dans le plan

Oxy

, les équations paramétriques du mouvement sont alors :

x-x_1=r \; \cos(ω \:t+ϕ)

;

y-y_1=±r \; \sin(ω \:t+ϕ)

;

z=v_z \: t

. Ainsi :

v_x=-r \:ω \; \sin(ω \:t+ϕ)

v_y=±r \:ω \; \cos(ω \:t+ϕ)

.
• Par comparaison avec les conditions initiales sur la vitesse, on obtient respectivement

ϕ=0

π

v_{0y}=±r \:ω

(

ϕ=π

q \:v_{0y}>0

;

ϕ=0

q \:v_{0y}<0

), ce qui donne

\displaystyle r=\frac{\left|v_{0y} \right|}{ω}

.
• Par comparaison avec les conditions initiales sur la position, on obtient

\displaystyle x_1=x_0+\frac{v_{0y}}{ω}

y_1=0

, c’est-à-dire :

\displaystyle x=\left(x_0+\frac{v_{0y}}{ω}\right)-\frac{v_{0y}}{ω} \: \cos(ω \:t)

\displaystyle y=\frac{v_{0y}}{ω} \: \sin(ω \:t)

Spectrographe de masse de Dempster

• Accélérés par le champ électrique, sous une tension

U=1000 \:\mathrm{V}

, les ions acquièrent une énergie cinétique :

\frac{1}{2} m \:v^2=q \:U

(en comparaison, on suppose négligeable leur énergie cinétique initiale, due à l'agitation thermique ; par ailleurs l'énergie finale est visiblement non relativiste puisque l'énergie de masse des ions est

≈20 \:m_p \: c^2≈20 \:\mathrm{GeV}

).
• Sous l'effet de la force magnétique

\overset{→}{F}=q \:\overset{→}{v} × \overset{→}{B}

perpendiculaire à

\overset{→}{B}

, le mouvement ne peut pas acquérir une composante parallèle à

\overset{→}{B}

; or la vitesse initiale est perpendiculaire à

\overset{→}{B}

, donc le mouvement se fait entièrement dans le plan perpendiculaire à

\overset{→}{B}

et passant par la position d'entrée dans le dispositif.
• La force est perpendiculaire à

\overset{→}{v}

, donc l'accélération tangentielle est nulle et le mouvement est uniforme. Enfin, l'accélération normale est

\displaystyle a_n=\frac{v^2}{R}=\frac{q \:v \:B}{m}

constante (en norme), donc le rayon de courbure de la trajectoire est constant, ainsi la trajectoire est une portion de cercle de rayon

\displaystyle R=\frac{m \:v}{q \:B}

.
• Compte tenu de la forme du dispositif et de l'orthogonalité de la vitesse initiale par rapport à la face d'entrée rectiligne, les trajets parcourus sont des demi-cercles. Les points d'impact, diamétralement opposés au point d'entrée, en sont donc distants d'un diamètre :

\displaystyle D=2 \,\frac{m \:v}{q \:B}=\frac{1}{B} \,\sqrt{\frac{8 \,m \:U}{q}}

.
• Numériquement :

D_1=40\text{,}7 \:\mathrm{cm}

pour

{}^{20}\mathrm{Ne}

D_2=42\text{,}7 \:\mathrm{cm}

pour

{}^{22}\mathrm{Ne}

• En considérant :

\displaystyle ∆D=\frac{2 \,m}{q \:B} \, ∆v=\frac{D}{v} \, ∆v

, l'observation de “zones” d'impact distinctes impose :

\displaystyle A_1 A_2=D_2-D_1> ∆D_1+∆D_2≈(D_1+D_2) \, \frac{∆v}{v}

c'est-à-dire :

\displaystyle \frac{∆v}{v}<\frac{D_2-D_1}{D_1+D_2}≈0\text{,}024

.
◊ remarque : compte tenu de :

\displaystyle D=\frac{1}{B} \,\sqrt{\frac{8 \,m \:U}{q}}

, cela donne

\displaystyle \frac{∆v}{v}<\frac{∆(\sqrt{m}\,)}{2 \:\sqrt{m}}=\frac{∆m}{4 \,m}

; ou inversement, la résolution du dispositif est caractérisée par une incertitude sur la masse :

\displaystyle \frac{∆m}{m}=4 \frac{∆v}{v}

Expérience de J.J. Thomson

• Les ions sont soumis à la force :

\overset{→}{F}=q.(\overset{→}{E}+\overset{→}{v} × \overset{→}{B} \:)

, en comparaison de laquelle leur poids peut être négligé. En supposant le problème non relativiste, on peut écrire la relation fondamentale de la dynamique de translation en projection sur les trois axes :

m \:\ddot{x}=q \:B \:\dot{y}

;

m \:\ddot{y}=-q \:B \:\dot{x}

;

m \:\ddot{z}=q \:E

.
• Compte tenu des conditions initiales, l'intégration de la troisième équation donne :

\displaystyle \dot{z}=\frac{q \:E}{m} \, t

puis

\displaystyle z=\frac{q \:E}{2 \,m} \, t^2

(en prenant l'origine au point d'entrée dans le dispositif).
• L'intégration des deux premières équations donne :

m \:\dot{x}=q \:B \:y+m \:v_0

m \:\dot{y}=-q \:B \:x

. On peut en déduire :

\displaystyle \ddot{x}+\left(\frac{q \:B}{m}\right)^2 x=0

\displaystyle y=\frac{m}{q \:B} \: (\dot{x}-v_0 )

.
• L'équation différentielle du second ordre en

x

a pour solution générale :

x=X \; \cos(ω \:t)+X' \; \sin(ω \:t)

avec

\displaystyle ω=\frac{q \:B}{m}

et où

X

X'

sont deux constantes dépendant des conditions initiales. Pour

t=0

on sait que

x=0

donc

X=0

. On en déduit :

\dot{x}=X' \:ω \; \cos(ω \:t)

et donc

\displaystyle X'=\frac{v_0}{ω}

. On obtient ainsi :

\displaystyle x=\frac{v_0}{ω} \: \sin(ω \:t)

\dot{x}=v_0 \; \cos(ω \:t)

, puis :

\displaystyle y=\frac{v_0}{ω} \: [\cos(ω \:t)-1]

.
• Si on considère que :

\displaystyle L≪\frac{m \:v_0}{q \:B}=\frac{v_0}{ω}

, alors la relation :

\displaystyle x=\frac{v_0}{ω} \: \sin(ω \:t)

montre que

\sin(ω \:t)≪1

et on peut faire l'approximation :

\sin(ω \:t)≈ω \:t

. Dans ces conditions, on peut écrire :

x≈v_0 \: t

\displaystyle y≈\frac{v_0}{ω} \: \left[\left(1-\frac{ω^2 \: t^2}{2}\right)-1\right]=-\frac{1}{2} v_0 \: ω \:t^2

.
◊ remarque : on utilise un développement à l'ordre

2

pour le cosinus car c'est le terme non nul d'ordre le plus bas pour

y

; on ne prend pas en compte de terme d'ordre

2

pour

x

car le terme correspondant du développement du sinus est nul.
• En particulier pour

x=L

on obtient :

\displaystyle t≈\frac{L}{v_0}

puis

\displaystyle z≈\frac{q \:E \:L^2}{2 \,m \:v_0^{\:2}}

\displaystyle y≈-\frac{ω \:L^2}{2 \,v_0}=-\frac{q \:B \:L^2}{2 \,m \:v_0}

.
◊ remarque : l'effet sur

z

est proportionnel à

\displaystyle \frac{E}{ℰ_{c0}}

(rapport à l'énergie cinétique) et l'effet sur

y

est proportionnel à

\displaystyle \frac{B}{p_0}

(rapport à la quantité de mouvement).

• Le “canon à ions” qui crée le faisceau peut focaliser les ions mais il subsiste une incertitude sur

v_0

due en particulier à l'agitation thermique des atomes initiaux. Les différents

v_0

donnent des

y

z

différents, mais reliés par l'expression :

\displaystyle z≈\frac{q \:E \:L^2}{2 \,m \:v_0^{\:2}}

avec

\displaystyle v_0≈-\frac{q \:B \:L^2}{2 \,m \:y}

, donc :

\displaystyle z≈\frac{2 \,m \:E}{L^2 \: B^2 \: q} \: y^2

. Cette expression correspond à l'équation d'un arc de parabole dans le plan des

(y,z)

• Les différents isotopes ont des masses différentes, donc pour

B

L

q

fixés, mais en l'absence du champ électrique (spectrographe “ordinaire”), ils donnent des taches différentes (proportionnellement à

\displaystyle \frac{1}{m}

) selon la direction de l'axe des

y

. Toutefois, deux taches sur l'écran peuvent être causées par des masses différentes, mais aussi par des vitesses

v_0

différentes ; on ne peut pas conclure (et on peut ne même pas le voir si les taches sont peu décalées et se superposent plus ou moins).
• Au contraire ici, pour

E

B

L

q

fixés, deux isotopes donnent des arcs de parabole différents (proportionnellement à

m

) selon la direction de l'axe des

z

; on peut les distinguer même s'ils ont des

y

égaux à cause de

v_0

plus ou moins différents.
◊ remarque : les différentes charges des ions (

q=n \:\left|q_e \right|

) donnent aussi des arcs de parabole différents, mais ces arcs sont nettement distincts et correspondent, pour chaque isotope, à une famille d'arcs dont les ordonnées varient proportionnellement à

\displaystyle \frac{1}{n}

; par contre, les différences de masses des isotopes causent de légers décalages : chaque arc d'une “famille” (en fonction de

n

) est dédoublé par la présence de deux isotopes.

Systèmes d'équations couplées

1.a.	• Les protons sont soumis à la force : $\overset{→}{F}=q.(\overset{→}{E}+\overset{→}{v} × \overset{→}{B} \:)$ ; la relation fondamentale de la dynamique de translation s'écrit : $m \:\overset{→}{a}=\overset{→}{F}=q \:E \:\overset{→}{u}_z+q \:B \:\overset{→}{v} × \overset{→}{u}_y$ . • Avec les notations de l'énoncé, on en déduit en projection sur les trois axes : $\ddot{x}=-ω \:\dot{z}$ ; $\ddot{y}=0$ ; $\ddot{z}=R \:ω^2+ω \:\dot{x}$ .

1.b.	• Compte tenu de la condition initiale $\dot{y}(0)=0$ , la relation : $\ddot{y}=0$ s'intègre en $\dot{y}=0$ ; avec la condition initiale $y(0)=0$ , ceci s'intègre en $y=0$ . Le mouvement se fait donc dans le plan $(Oxz)$ . • Ceci est prévisible “géométriquement” : la particule étant initialement immobile, la force se limite initialement à la composante électrostatique et le mouvement commence selon l'axe $(Oz)$ ; la composante magnétique de la force peut ensuite dévier le mouvement, mais perpendiculairement au champ magnétique, donc selon le plan $(Oxz)$ .

2.a.	• Les deux équations sont couplées (elles font intervenir à la fois $x$ et $z$ ) ; pour en déduire une combinaison “découplée”, il est donc impossible de ne faire intervenir que l'une des deux (ce qui correspondrait à un coefficient nul pour l'autre). Or, si une combinaison convient avec des coefficients $α$ et $β$ , tout couple de coefficients proportionnels à $(α \,; β)$ convient aussi ; donc si $α≠0$ on peut utiliser $\left(1 \,; \frac{β}{α}\right)$ et il suffit alors de renommer $β$ le second coefficient pour simplifier.

2.b.	• La combinaison obtenue correspond à : $\ddot{x}+β \:\ddot{z}=ω.(β \:\dot{x}-\dot{z} )+β \:R \:ω^2$ . • Pour que l'équation se ramène à la variable $u=x+β \:z$ uniquement, il faut et il suffit que la combinaison du membre de droite soit proportionnelle à $\dot{u}$ . Ceci peut s'écrire par exemple en égalant les rapports : $\displaystyle \frac{1}{β}=\frac{β}{-1}$ ou bien avec le déterminant : $\begin{vmatrix} 1 & β \\ β & -1 \end{vmatrix}=0$ ; on aboutit ainsi à la condition : $β^2=-1$ .

2.c.	• L'équation précédente a pour solutions : $β=± \mathrm{i}$ . La variable cherchée peut donc s'écrire sous la forme : $u=x+\mathrm{i} \:z$ . ◊ remarque : dans le cas général (mathématique) on obtient deux solutions indépendantes ( $u'$ et $u''$ ), on intègre les deux équations “découplées” vérifiées par ces variables, puis on calcule les deux inconnues (ici $x$ et $z$ ) en fonction de $u'$ et $u''$ ; mais dans ce cas particulier, les deux solutions sont des conjugués complexes donc il suffit de résoudre une équation puis de considérer la partie réelle et la partie imaginaire. • L'équation vérifiée par cette variable s'écrit : $\ddot{u}=\mathrm{i} \:ω \:\dot{u}+\mathrm{i} \:R \:ω^2$ ; c'est une équation différentielle linéaire du premier ordre par rapport à $\dot{u}$ . Les solutions sont de la forme : $\dot{u}(t)=-R \:ω+V \:\mathrm{e}^{\mathrm{i}ωt}$ où $V$ est une constante d'intégration. D'après la condition initiale $\dot{u}(0)=0$ (vitesse initiale nulle) : $0=-R \:ω+V$ ; ainsi : $\dot{u}(t)=R \:ω .\left(\mathrm{e}^{\mathrm{i}ωt}-1\right)$ . • La seconde intégration donne : $u(t)=-R \:ω \:t-\mathrm{i} \:R \:\mathrm{e}^{\mathrm{i}ωt}+U$ où $U$ est une constante d'intégration. D'après la condition initiale $u(0)=0$ (départ de l'origine) : $0=-\mathrm{i} \:R+U$ ; on obtient ainsi : $u(t)=-R \:ω \:t+\mathrm{i} \:R .\left(1-\mathrm{e}^{\mathrm{i}ωt} \, \right)$ . • Ceci donne finalement : $x=\mathrm{Re}(u)=-R \:ω \:t+R \; \sin(ω \:t)$ ; $z=\mathrm{Im}(u)=R-R \; \cos(ω \:t)$ .

2.d.	• Les expressions précédentes décrivent un point en rotation (dans le sens “anti-horaire”) sur un cercle, de rayon $R$ , dont le centre $C$ se déplace selon le mouvement de translation uniforme : $x_C=-R \:ω \:t$ ; $z_C=R$ . Pour $M$ , c'est le mouvement décrit par un point donné du cercle qui roule sans glisser sur l'axe $(Ox)$ ; la courbe est une cycloïde. ◊ remarque : $ω=4\text{,}8.{10}^7 \: \mathrm{rad.s^{-1}}$ ; $R=8\text{,}35.{10}^{-3} \: \mathrm{m}$ ; $v_{Cx}=-R \:ω=- 4\text{,}0.{10}^5 \: \mathrm{m.s^{-1}}$ . ◊ remarque : si on ne connaît pas la cycloïde, il est simple de tracer proprement la courbe en prenant quelques points particuliers : $ω \:t=\frac{π}{6} \,;\, \frac{π}{4} \,;\, \frac{π}{3} \,;\, \frac{π}{2} \;⋯$ et en utilisant les symétries trigonométriques.

B. EXERCICE D'APPROFONDISSEMENT

Principe de relativité de Galilée

• D’après ce principe, on montre le lien entre les champs électrique et magnétique (non relativistes) ; pour un changement de référentiel galiléen :

$\overset{→}{F}=q.\left(\overset{→}{E}+\overset{→}{v} × \overset{→}{B} \,\right)$ dans $ℛ$ et $\overset{→}{F}'=q.\left(\overset{→}{E}'+\overset{→}{v}' × \overset{→}{B}' \,\right)$ dans $ℛ'$ ;
avec $\overset{→}{v}=\overset{→}{v}_e+\overset{→}{v}'$ .

• On obtient par comparaison :

\overset{→}{B}'=\overset{→}{B}

\overset{→}{E}'=\overset{→}{E}+\overset{→}{v}_e × \overset{→}{B}

.
• Ceci montre qu’il s’agit d’un effet “électromagnétique” dont la signification physique est globale, où la séparation entre une partie électrique et une partie magnétique est d'une certaine façon arbitraire (elle dépend du référentiel).