MESURE DU QUOTIENT e/m POUR LES ÉLECTRONS

MESURE DU QUOTIENT $e/m$ POUR LES ÉLECTRONS - corrigé du TP

Dispositif expérimental

Champ magnétique

◊ remarque : l'étude détaillée du champ magnétique fait l'objet d'un autre TP.

Faisceau d’électrons

• D'après le théorème de l'énergie cinétique, l'accélération des électrons par une tension

U

leur donne une énergie cinétique

ℰ_c=e \:U

(la pesanteur et l'énergie cinétique initiale sont négligeables). La vitesse des électrons du faisceau est donc :

\displaystyle v=\sqrt{\frac{2 \,e \:U}{m}}

Mesures

Étude en fonction de la tension accélératrice

• Pour

I=1\text{,}5 \:\mathrm{A}

(donc pour un champ donné :

B=1\text{,}17±0\text{,}03 \:\mathrm{mT}

) et pour

100 \:\mathrm{V}≤U≤300 \:\mathrm{V}

, on vérifie expérimentalement que le carré du diamètre est proportionnel à la tension (

\displaystyle D^2=\frac{8 \,m}{e \:B^2} \, U

) :

• Le coefficient de proportionnalité est :

a=(32\text{,}1±0\text{,}7).{10}^{-6} \: \mathrm{m^2.V^{-1}}

; on en déduit le quotient :

$\displaystyle \frac{e}{m}=\frac{8 \,U}{D^2 \: B^2}=\frac{8}{a \:B^2}=(1\text{,}82±0\text{,}15).{10}^{11} \: \mathrm{C.kg^{-1}}$ .

Cette valeur est tout à fait compatible avec celle généralement admise par la communauté scientifique :

\displaystyle \frac{e}{m}=1\text{,}759.{10}^{11} \: \mathrm{C.kg^{-1}}

[Physical Review, 1994, vol. D50, n° 3, p. 1233].

Étude en fonction du champ magnétique

• Pour

U=75 \:\mathrm{V}

;

100 \:\mathrm{V}

;

197 \:\mathrm{V}

respectivement (donc pour une vitesse donnée) et pour

0\text{,}75≤I≤1\text{,}5 \:\mathrm{A}

1\text{,}0≤I≤2\text{,}5 \:\mathrm{A}

, on peut vérifier expérimentalement que le diamètre est proportionnel à l’inverse du champ magnétique (

\displaystyle D=\sqrt{\frac{8 \,m \:U}{e}} \: \frac{1}{B}

) :

• Les coefficients sont respectivement :

$a'=(51\text{,}4±3\text{,}5).{10}^{-6} \: \mathrm{m.T}$ ; $a'=(60\text{,}0±2\text{,}3).{10}^{-6} \: \mathrm{m.T}$ ; $a'=(93\text{,}1±1\text{,}5).{10}^{-6} \: \mathrm{m.T}$ .

• On en déduit

\displaystyle \frac{e}{m}=\frac{8 \,U}{D^2 \: B^2}=\frac{8 \,U}{{a'}^2}

$\displaystyle \frac{e}{m}=(2\text{,}27±0\text{,}31).{10}^{11} \: \mathrm{C.kg^{-1}}$ ; $(2\text{,}22±0\text{,}18).{10}^{11} \: \mathrm{C.kg^{-1}}$ ; $(1\text{,}82±0\text{,}06).{10}^{11} \: \mathrm{C.kg^{-1}}$ .

• Certains de ces résultats sont très imprécis, mais l'ensemble est raisonnablement compatible avec la valeur généralement admise par la communauté scientifique :

\displaystyle \frac{e}{m}=(1\text{,}7588196±0\text{,}0000016).{10}^{11} \: \mathrm{C.kg^{-1}}

.

◊ remarque : l’étude expérimentale est ici plus difficile, car on ne peut ni trop diminuer

B

(mesures trop imprécises), ni trop augmenter

B

(échauffement excessif des bobines) ; il semble toutefois que les mesures soient moins perturbées pour les valeurs plus grandes de

U

I

.

◊ remarque : parmi les différentes causes d'incertitude (pour tout le TP), on peut citer :

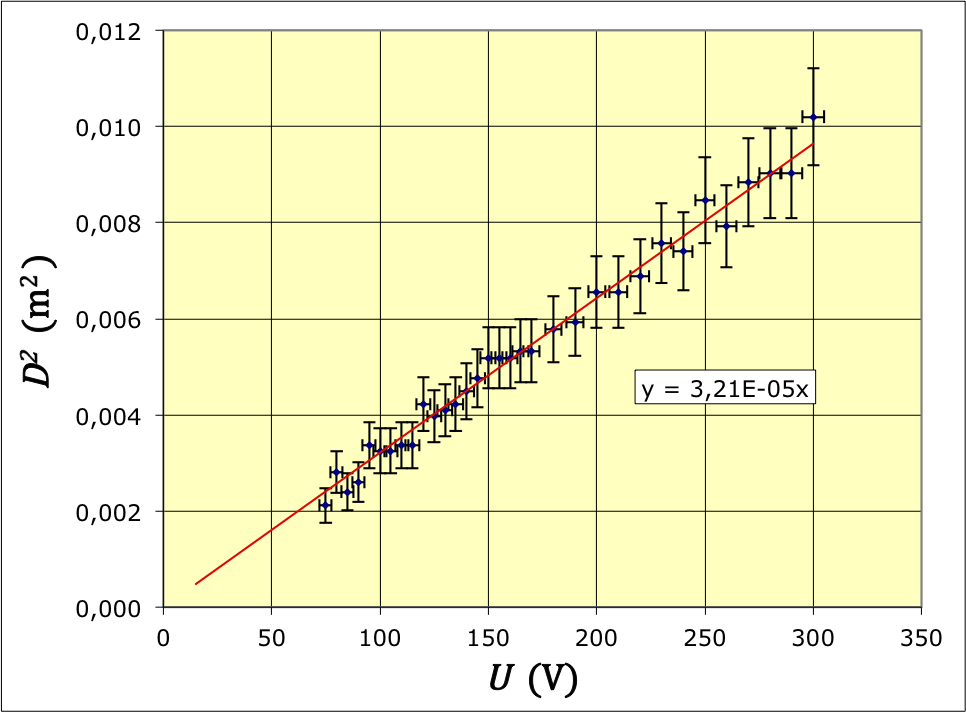
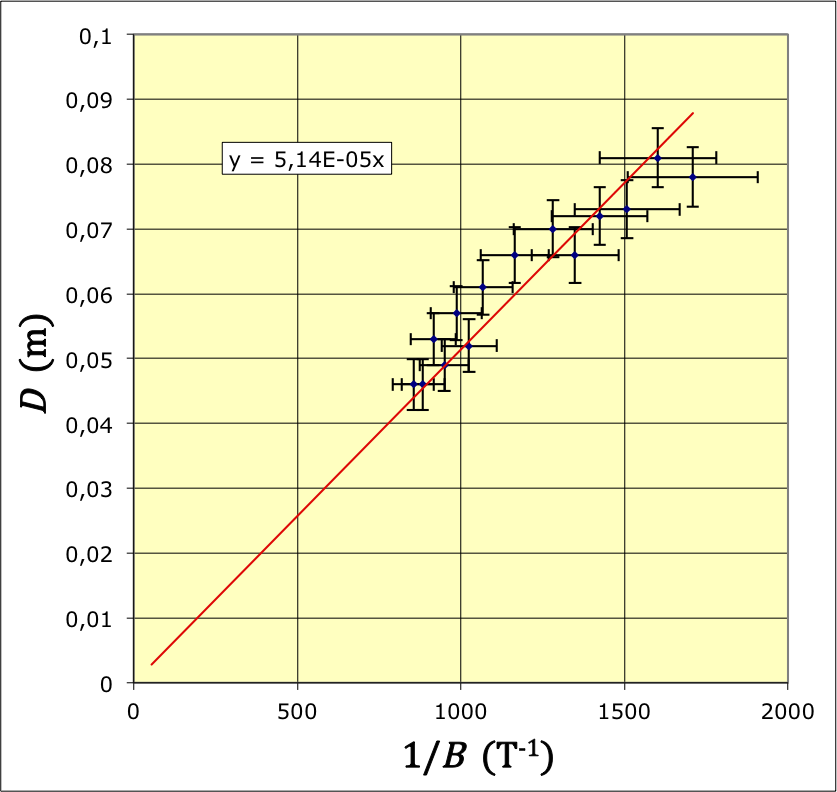
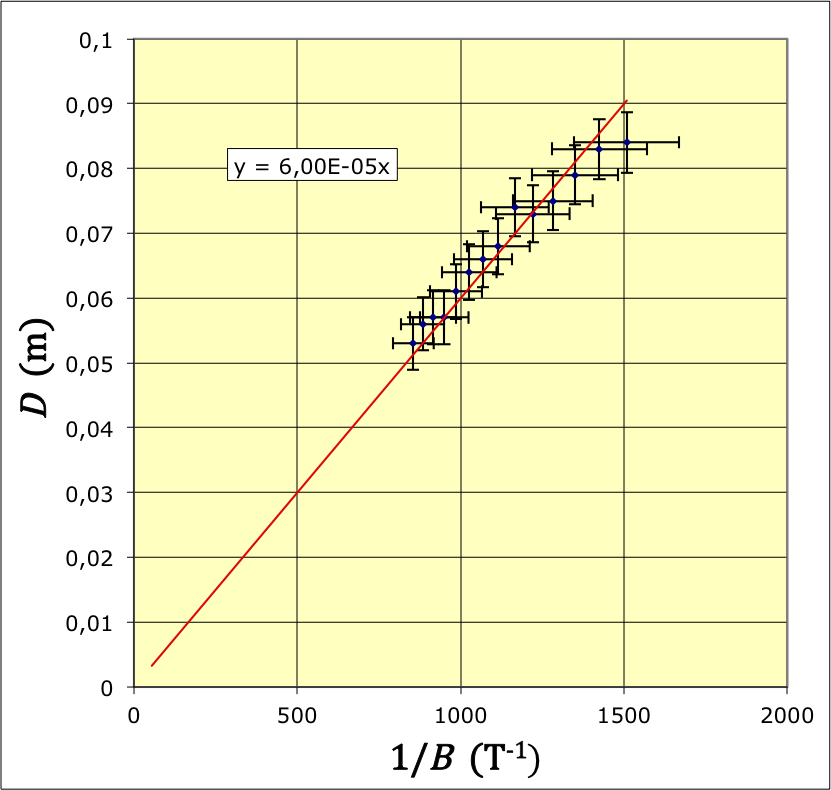
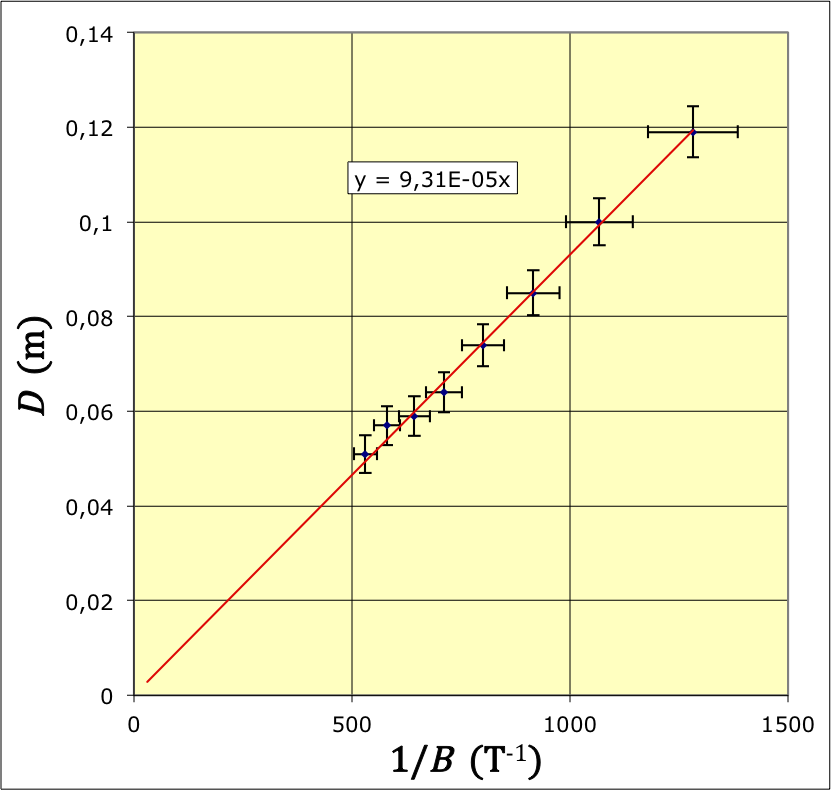
◊	pour $B$ faible, le champ terrestre est alors moins négligeable ;
◊	pour $D$ grand, le champ $B$ est moins uniforme ;
◊	pour $D$ grand, la charge électrostatique éventuelle du verre de l’ampoule risque de créer un champ électrique parasite ;
◊	pour $D$ grand, le bord de l'ampoule se comporte comme une lentille divergente avec d'importants défauts d'optique ;
◊	etc…