DIPÔLE ÉLECTROSTATIQUE - corrigé des exercices

A. EXERCICES DE BASE

I. Lignes de champ

• Dans un plan, une courbe est caractérisée par une équation, éventuellement une équation différentielle si on définit la courbe par ses propriétés locales. C'est le cas en particulier pour les lignes de champ.
• Les lignes de champ sont caractérisées par la propriété :

d\overset{⟶}{OM}∥\overset{→}{E}

; or les coordonnées polaires (avec lesquelles est décrit

\overset{→}{E}

dans l'énoncé) correspondent à :

d\overset{⟶}{OM}=dr \;\overset{→}{u}_r+r \:dθ \;\overset{→}{u}_θ

et donc l'équation différentielle cherchée est :

\displaystyle \frac{dr}{E_r} =\frac{r \:dθ}{E_θ}

.
• La relation précédente s'écrit :

\displaystyle \frac{dr}{r}=\frac{2 \;\cos(θ)}{\sin(θ)} \: dθ

; qui s'intègre en :

\ln(r)=2 \; \ln\left(\left|sin(θ) \right|\right)+Cste

. On en déduit l'équation des lignes de champ :

r=a \; \sin^2(θ)

avec

a>0

constante d’intégration.

• Dire que

\overset{→}{E}

dérive d'un potentiel

V

correspond à écrire :

\overset{→}{E}=-\overset{→}{∇}\, V

.
• Le gradient est par définition tel que :

dV=\overset{→}{∇}\, V ∙d\overset{⟶}{OM}

; en coordonnées polaires, ceci peut s'écrire :

\displaystyle \frac{∂V}{∂r} \: dr+\frac{∂V}{∂θ} \: dθ=\overset{→}{∇} \, V ∙\left(dr \;\overset{→}{u}_r+r \:dθ \;\overset{→}{u}_θ \right)

; ceci impose :

\displaystyle \overset{→}{∇} \,V=\frac{∂V}{∂r} \: \overset{→}{u}_r+\frac{1}{r} \frac{∂V}{∂θ} \: \overset{→}{u}_θ

.
• On obtient ainsi :

\displaystyle \frac{∂V}{∂r}=-E_r=-\frac{2 \,k \:\cos(θ)}{r^3}

\displaystyle \frac{1}{r} \frac{∂V}{∂θ}=-E_θ=-\frac{k \:\sin(θ)}{r^3}

.
• Pour simplement montrer que le champ dérive d'un potentiel

V

, on peut montrer que la différentielle

\displaystyle dV=-\overset{→}{E}∙d\overset{⟶}{OM}=-\frac{2 \,k \:\cos(θ)}{r^3} \: dr-\frac{k \:\sin(θ)}{r^2} \: dθ

est une différentielle “totale” (c'est-à-dire qu'il existe effectivement une fonction

V

correspondante). Dans ce cas, puisque les variables

r

θ

sont indépendantes, les dérivées “croisées” sont égales :

\displaystyle \frac{∂^2 V}{∂r \,∂θ}=\frac{∂^2 V}{∂θ \,∂r}

; or cette propriété est effectivement vérifiée :

\displaystyle \frac{∂}{∂θ} \left(-\frac{2 \,k \:\cos(θ)}{r^3} \right)=\frac{∂}{∂r} \left(-\frac{k \:\sin(θ)}{r^2} \right)=\frac{2 \,k \:\sin(θ)}{r^3}

.
• Pour calculer

V

il faut intégrer

dV

. De

\displaystyle \frac{∂V}{∂r}=-\frac{2 \,k \:\cos(θ)}{r^3}

on déduit :

\displaystyle V=\frac{k \:\cos(θ)}{r^2} +α(θ)

où

α(θ)

est une constante d’intégration par rapport à la variable

r

, mais pouvant dépendre de

θ

. En reportant dans l'autre équation on obtient :

\displaystyle \frac{∂V}{∂θ}=-\frac{k \:\sin(θ)}{r^2} +\frac{dα}{dθ}=-\frac{k \:\sin(θ)}{r^2}

donc :

\displaystyle \frac{dα}{dθ}=0

α=Cste

.
• Choisissant par convention

α=0

pour retrouver

V→0

quand

r→∞

, on obtient :

\displaystyle V=\frac{k \:\cos(θ)}{r^2}

II. Champ et flux

• Les courbes équipotentielles ont des équations de la forme

V(r,θ)=A

, où

A

est la valeur constante du potentiel sur l'équipotentielle considérée.

◊ remarque : les équipotentielles sont dans ce cas homothétiques les unes des autres, celles correspondant aux plus grandes valeurs absolues du potentiel sont plus “proches” de l'origine.

• On peut par exemple tracer ces équipotentielles en reportant, pour chaque direction

θ

, une distance à l'origine :

$\displaystyle r=\sqrt[3]{\frac{k}{A} \: \left(3 \:\cos^2(θ)-1\right)}$ .

dipoleElStat_cor_Im/dipoleElStat_cor_Im1.jpg

◊ remarque : dans l'espace, les “équipotentielles” sont des surfaces ; les “courbes” équipotentielles envisagées par l'énoncé sont les intersections de ces surfaces avec le plan du dessin (plan contenant

Oz

) car l'ensemble est invariant par rotation d'axe

Oz

(les surfaces équipotentielles sont donc des surfaces de révolution, engendrées par la rotation autour de

Oz

des courbes décrites ici).

• Le champ

\overset{→}{E}=-\overset{→}{∇}\, V

a pour coordonnées polaires :

$\displaystyle E_r=-\frac{∂V}{∂r}=\frac{3 \,k.\left(3 \;\cos^2(θ)-1\right)}{r^4}$ et $\displaystyle E_θ=-\frac{1}{r} \frac{∂V}{∂θ}=\frac{6 \,k \;\sin(θ) \: \cos(θ)}{r^4}$ .

• D'après l'énoncé, le champ possède une symétrie de révolution autour de

Oz

; ceci ne signifie pas qu'il est indépendant de l'angle

ϕ

, mais seulement que ses coordonnées en sont indépendantes : le vecteur en dépend car les vecteur de base en dépendent. Si on change

ϕ

le vecteur

\overset{→}{E}

tourne comme la base et garde les mêmes coordonnées. Le potentiel est alors indépendant de

ϕ

; donc

E_ϕ=0

• Le flux à travers une calotte sphérique se limite à celui de la composante radiale :

$\displaystyle Φ=∫ \,\overset{→}{E}∙d\overset{→}{S}=∫ \,E_r \: dS=∬ \,\frac{3 \,k.\left(3 \,\cos^2(θ)-1\right)}{r^4} \: r^2 \: \sin(θ) \: dθ \:dϕ$ ;
$\displaystyle Φ=\frac{3 \,k}{r^2} \left[∫_0^α \left(3 \,\cos^2(θ)-1\right) \: \sin(θ) \: dθ\:\right] \; \left(∫_0^{2π} dϕ\right)=\frac{6π \,k}{r^2} \, ∫_{\cos(α)}^1 (3 \,u^2-1) \: du$ ;
$\displaystyle Φ=\frac{6π \,k}{r^2} \: \sin^2(α) \: \cos(α)$ .

• En particulier :

Φ=0

pour

α=\frac{π}{2}

;

Φ=0

pour

α=π

III. Tracé d'un diagramme électrique

• En se limitant au plan

xOy

, on peut considérer les coordonnées des trois points :

$\left(x_A=0 \; ; \,y_A=a\right)$ ; $\displaystyle \left(x_B=-\frac{a \:\sqrt{3}}{2} \; ; \, y_B=-\frac{a}{2}\,\right)$ ; $\displaystyle \left(x_C=\frac{a \:\sqrt{3}}{2} \; ; \, y_C=-\frac{a}{2}\,\right)$ .

• Le potentiel peut être écrit sous la forme suivante, dont l'exploitation pratique est toutefois peu évidente :

\displaystyle V(x,y)=\frac{q}{4π \:ε_0} \: ∑ \frac{1}{\sqrt{(x-x_i )^2+(y-y_i )^2}}

.
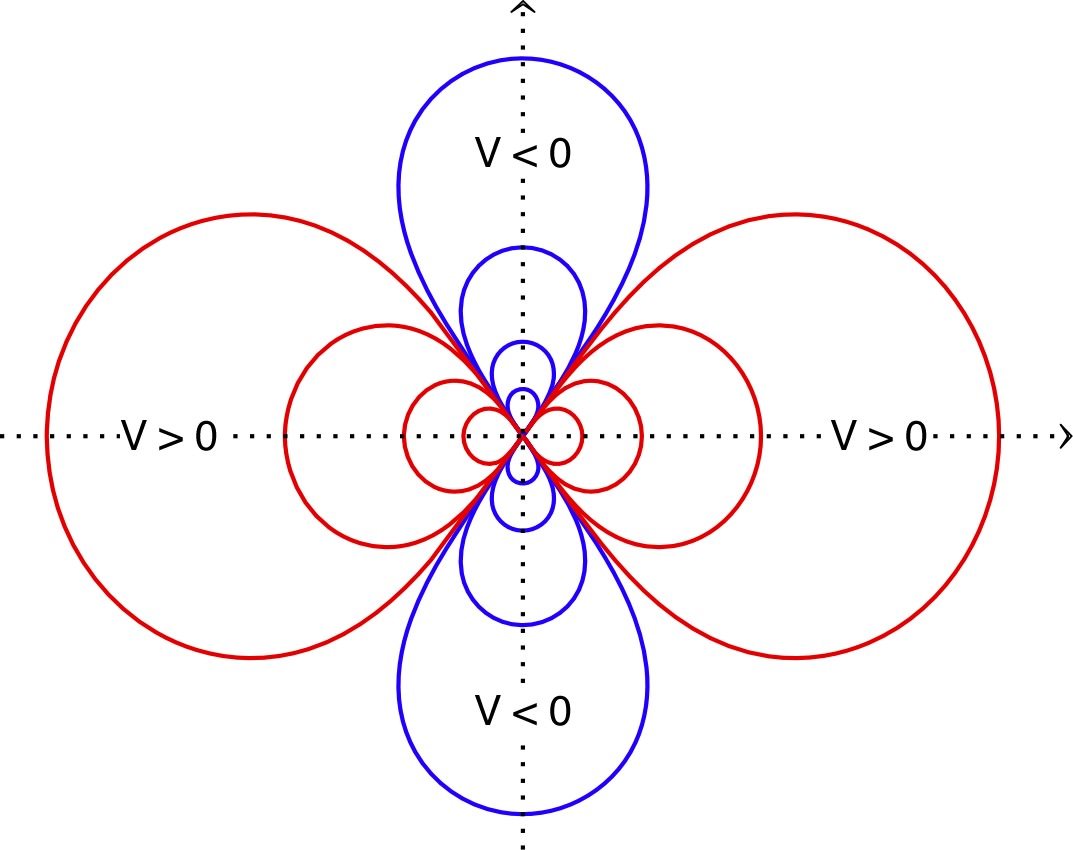
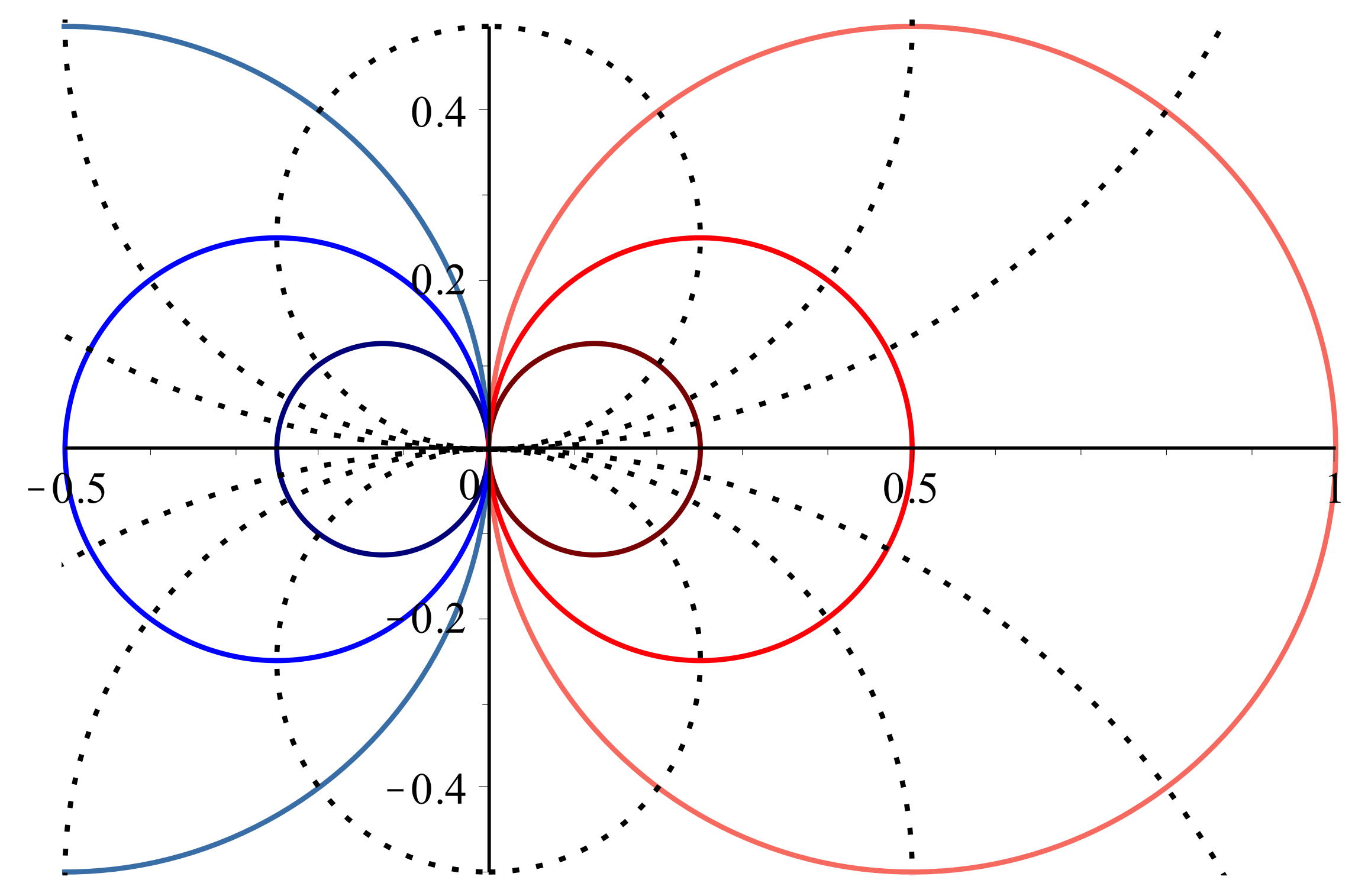
• Qualitativement, l’allure des équipotentielles au voisinage de chaque charge (“loin” des autres charges) est semblable à l’allure de celles d’une charge isolée (cercles concentriques autour de chacune des charges). Les lignes de champ, orthogonales aux équipotentielles, sont alors radiales orientées “vers l'extérieur” par rapport à la charge correspondante.

dipoleElStat_cor_Im/dipoleElStat_cor_Im2.jpg

◊ remarque : on raisonne ici sur des “lignes équipotentielles”, qui ne sont que les intersections du plan

xOy

avec les surfaces équipotentielles dans l’espace.
• De même, puisque les trois charges sont positives, on doit retrouver des lignes concentriques autour de

G

pour l’ensemble considéré à grande distance (

a

est alors négligeable en proportion). On retrouve de même alors des lignes de champ radiales autour de

G

, orientées vers l'extérieur.

• On peut préciser qu'entre deux charges (la troisième, plus éloignée étant omise en première approximation) il doit y avoir deux lignes de champ (symétriques par rapport à la médiatrice) qui convergent vers un même point : de part et d'autre, les lignes peuvent s'écarter sur les côtés, mais entre les deux il y en a forcément deux qui ne peuvent privilégier ni un côté ni l'autre... Puisqu'elles sont orientées en sens inverse, le champ ne peut que s'annuler au point de rencontre ; il y a ainsi trois points où le champ est nul, au voisinage des milieux des côtés du triangle.
• En outre, par symétrie, le champ en

G

est forcément nul.

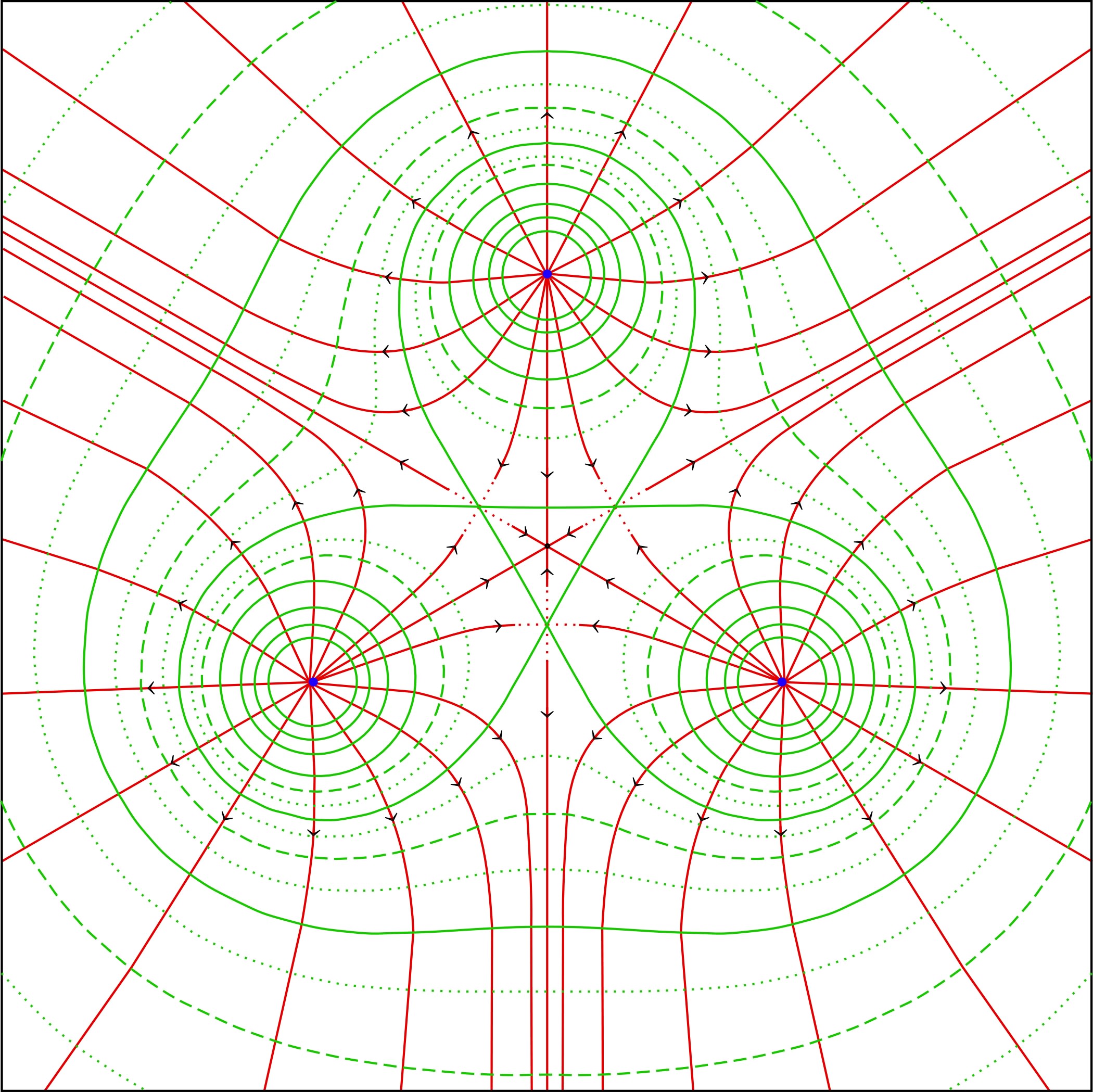
• Le diagramme ci-dessus, obtenu par un calcul plus précis (non demandé ici) montre l’existence de trois “minimums relatifs” au voisinage des milieux des côtés du triangle ; en réalité, il ne s’agit que d’un minimum relatif par rapport aux déplacements d'un sommet à l'autre : c’est un maximum relatif par rapport aux déplacements selon la médiatrice correspondante.
• On observe de même un “minimum relatif” du potentiel au centre ; en réalité, il ne s’agit que d’un minimum relatif par rapport aux coordonnées

x

y

: c’est un maximum relatif par rapport à

z

et ce n’est donc pas un extremum “dans l’espace”.

• En considérant les points de l’axe

Oy

(où

E_x=0

par symétrie) :

$\displaystyle V(0,y)=\frac{q}{4π \:ε_0} \: \left[\frac{1}{|y-a|} +\frac{2}{\sqrt{\left(\frac{a \:\sqrt{3}}{2}\right)^2+\left(y+\frac{a}{2}\right)^2}}\right]$ ;
$\displaystyle E_y (0,y)=-\frac{∂V}{∂y}=\frac{q}{4π \:ε_0} \: \left[\frac{\mathrm{sgn}(y-a)}{(y-a)^2} +\frac{2 \,y-a}{\left(\left(\frac{a \:\sqrt{3}}{2}\right)^2+\left(y+\frac{a}{2}\right)^2 \right)^{3/2}} \right]$ .

• Compte tenu du fait que les points d’annulation sont (relativement) proches de l’origine (en particulier

y<a

), on peut chercher leur position en développant par rapport à

\displaystyle \frac{y}{a}

$\displaystyle V(0,y)≈\frac{q}{4π \:ε_0} \: \frac{3}{a} \: \left(1+\frac{y^2}{4 \,a^2}+\frac{5 \,y^3}{8 \,a^3}\right)$ et donc $\displaystyle E_y (0,y)=-\frac{∂V}{∂y}≈\frac{q}{4π \:ε_0}\, \frac{3 \,y}{2 \,a^3} \: \left(1+\frac{15 \,y}{4 \,a}\right)$ .

◊ remarque : on peut aussi développer directement

E_y

à l’ordre

2

.
• Ceci correspond à une annulation du champ pour

y=0

(à l’origine) et pour

\displaystyle y≈-\frac{4 \,a}{15}≈-\text{0,27} \:a

. Compte tenu de l’invariance par rotation de

\frac{2π}{3}

on retrouve ainsi, en plus de l’origine, trois points d’annulation (soit quatre points au total).
◊ remarque : la résolution numérique directe indique une annulation pour

y≈-\text{0,285} \:a

(on pourrait aussi développer à l'ordre suivant) ; ceci montre la précision du résultat ainsi obtenu.

IV. Répartition surfacique de dipôles

• Un moment dipolaire

\overset{→}{p}

correspond en fait à la limite de deux charges

±q

séparées par une distance

d

et étudiées pour

d→0

avec

p=q \:d

constant. On peut de même considérer qu’une densité surfacique

μ

de moment dipolaire correspond à la limite de deux densités surfaciques de charges

±σ

séparées par une distance

d

et étudiées pour

d → 0

avec

μ=σ \:d

constant.
• Sur l’axe d’un disque de rayon

R

portant

σ

uniforme, le potentiel (calculé par intégration directe) est :

\displaystyle \underline{V}(x)=\frac{σ}{2 \,ε_0} \: \left(\sqrt{x^2+R^2}-|x|\right)

et le champ (parallèle à l’axe) est :

\displaystyle \underline{E}_x (x)=\frac{σ \:x}{2 \,ε_0} \: \left(\frac{1}{|x|} -\frac{1}{\sqrt{x^2+R^2}}\right)

.
• Pour deux disques d’abscisses

\displaystyle ±\frac{d}{2}

avec des densités surfaciques

±σ

, on obtient au total sur l’axe :

\displaystyle V(x)=\underline{V}\left(x-\frac{d}{2} \right)-\underline{V}\left(x+\frac{d}{2} \right)

dont la limite correspond à :

\displaystyle V(x)=-\frac{μ}{σ} \: \frac{d}{dx} \underline{V}(x)=\frac{μ \:x}{2 \,ε_0} \: \left(\frac{1}{|x|} -\frac{1}{\sqrt{x^2+R^2}}\right)

.
• On peut procéder de même pour le champ, ou bien considérer :

\displaystyle E_x (x)=-\frac{d}{dx} V(x)=\frac{μ}{2 \,ε_0} \, \frac{R^2}{\left(x^2+R^2 \right)^{3/2}}

V. Dipôle cylindrique

1.a.

• Si on sait que pour un fil réel (non infini) les équipotentielles sont des ellipsoïdes ayant les extrémités pour foyers, alors on comprend que l'assimilation à un cylindre n'est valable que très près du milieu. Par contre, pour la différence associée aux deux fils, la variation des ellipsoïdes est très semblable sur une proportion nettement moins restreinte de la longueur.

dipoleElStat_cor_Im/dipoleElStat_cor_Im5.jpg

dipoleElStat_cor_Im/dipoleElStat_cor_Im6.jpg

• Sinon on peut raisonner sur le champ électrique : pour deux fils portant des charges opposées, leurs contributions axiales respectives sont toujours de signes contraires, donc elles ont plus ou moins tendance à se compenser. L'utilisation du modèle théorique du fil “infini”, très médiocre de ce point de vue en particulier, peut alors être supposée acceptable (en se limitant tout de même au voisinage du milieu des fils :

r

z≪L

longueur réelle des fils).

dipoleElStat_cor_Im/dipoleElStat_cor_Im3.jpg

dipoleElStat_cor_Im/dipoleElStat_cor_Im4.jpg

1.b.

• Selon le modèle du fil rectiligne “infini”, le potentiel créé par le fil

(1)

à une distance

r_1

(calculé avec le théorème de Gauss) est de la forme :

\displaystyle V_1=-\frac{λ}{2π \:ε_0} \: \ln(r_1 )+{Cte}_1

; de même pour le fil

(2)

à une distance

r_2

\displaystyle V_2=-\frac{λ}{2π \:ε_0} \: \ln(r_2 )+{Cte}_2

.
• Le potentiel total est donc :

\displaystyle V(r_1 \, ,\:r_2)=\frac{λ}{2π \:ε_0} \: \ln\left(\frac{r_2}{r_1} \right)+{Cte}_2-{Cte}_1

; compte tenu de la référence choisie

V\left( \frac{d}{2} \, ,\,\frac{d}{2} \right)=0

sur

Oz

, on obtient :

\displaystyle V(r_1 \, ,\:r_2)=\frac{λ}{2π \:ε_0} \: \ln\left(\frac{r_2}{r_1} \right)

• Pour

d≪r

on obtient au premier ordre :

r_1^{\:2}≈r^2-r \:d \: \cos(θ)

r_2^{\:2}≈r^2+r \:d \: \cos(θ)

. Ceci donne :

\displaystyle V(r_1 \, ,\:r_2)≈\frac{λ}{4π \:ε_0} \: \ln\left(\frac{r^2+r \:d \:\cos(θ)}{r^2-r \:d \:\cos(θ)}\right)≈\frac{λ}{4π \:ε_0} \: \ln\left(1+2 \frac{d}{r} \, \cos(θ) \right)

puis à la limite :

$\displaystyle V(r,θ)≈\frac{λ \:d}{2π \:ε_0 \: r} \: \cos(θ)=\frac{p}{2π \:ε_0 \: r} \: \cos(θ)$ .

• On en déduit ensuite le champ :

\overset{→}{E}=E_r \; \overset{→}{u}_r+E_θ \; \overset{→}{u}_θ

(

E_z=0

d’après les symétries, dans l'approximation du modèle), avec :

\displaystyle E_r (r,θ)=-\frac{∂V}{∂r}≈\frac{p}{2π \:ε_0 \: r^2} \: \cos(θ)

\displaystyle E_θ (r,θ)=-\frac{1}{r} \, \frac{∂V}{∂θ}≈\frac{p}{2π \:ε_0 \: r^2} \: \sin(θ)

◊ remarque : les lignes de champ sont caractérisées par :

\displaystyle \frac{r^2 \: dr}{\cos(θ)} = \frac{r^2 \: r \:dθ}{\sin(θ)}

donc

\displaystyle \frac{dr}{r}=\frac{\cos(θ)}{\sin(θ)} \: dθ

et ainsi

r=a \; \sin(θ)

avec

a

constante d’intégration ; ce sont des cercles parallèles à

xOy

et centrés sur

Oy

, mais ce n'est qu'une approximation dipolaire ; les lignes de champ réelles relient les charges et ne peuvent pas être refermées sur elles mêmes (au niveau des fils).

B. EXERCICES D’APPROFONDISSEMENT

VI. Force de Keesom

• En considérant que le premier dipôle est dans le sens de l'axe, il crée au niveau du second un champ :

\displaystyle E_r=\frac{p_0}{2π \:ε_0 \: r^3}

(parallèle à l'axe).

• En considérant le second dipôle dans le même sens, il subit dans ce champ une force totale qui peut se calculer en ajoutant les forces subies par chaque charge :

\displaystyle F_r=q' \, \frac{p_0}{2π \:ε_0 \: r_{+}^{\:3}}-q' \, \frac{p_0}{2π \:ε_0 \: r_{-}^{3}}≈-\frac{3 \,p_0 \: p_0'}{2π \:ε_0 \: r^4}

.
• S'il est dans le même sens, le second dipôle est attiré vers la zone de champ plus fort ; s'il est de sens contraire il est repoussé avec une force de même norme.
◊ remarque : pour un dipôle permanent, on peut utiliser :

\overset{→}{F}=-\overset{→}{∇} ℰ_p=\overset{→}{∇}\left(\overset{→}{p}∙\overset{→}{E} \right)

; plus généralement, il faut considérer

\overset{→}{F}=\left(\overset{→}{p}∙\overset{→}{∇}\right) \, \overset{→}{E}

• Le moment

\overset{→}{ℳ}=\overset{→}{p} × \overset{→}{E}

correspond à :

dW=p \:E \; \sin(θ) \: dθ

. Le travail nécessaire pour retourner le second dipôle dans le champ du premier (passage de

θ=0

θ=π

) est donc :

W = 2 \,p \:E

.
◊ remarque : ceci se déduit aussi de l'énergie potentielle :

W=-∆ℰ_p

• Les proportions respectives de dipôles parallèles et antiparallèles sont :

$\displaystyle P_{+}=\frac{1}{1+\mathrm{e}^{-W/kT}}$ et $\displaystyle P_{-}=\frac{\mathrm{e}^{-W/kT}}{1+\mathrm{e}^{-W/kT}}$ avec $\displaystyle W=\frac{p_0 \: p_0'}{π \:ε_0 \: r^3}$ .

• Pour

W≪k \:T

\displaystyle P_{+}≈\frac{1}{2} \left(1+\frac{W}{2 \,k \:T}\right)

\displaystyle P_{-}≈\frac{1}{2} \left(1-\frac{W}{2 \,k \:T}\right)

.
• La force moyenne est donc :

\displaystyle 〈F_r 〉=P_{+} \: F_{+}+P_{-} \: F_{-}≈-\frac{3 \,p_0 \: p_0'}{2π \:ε_0 \: r^4} \: \frac{W}{2 \,k \:T}=-\frac{3}{4 \;k \:T} \: \left(\frac{p_0 \: p_0'}{π \:ε_0}\right)^2 \frac{1}{r^7}

.
◊ remarque : le calcul plus exact (intégrant sur tous les angles possibles) donne un coefficient

\displaystyle \frac{1}{4 \,k \:T}

VII. Force de Debye

• Le champ électrique (en

\mathrm{V.m^{-1}}

) est homogène à

\displaystyle \frac{q}{4π \:ε_0 \: r^2}

(avec la permittivité en

\mathrm{F.m^{-1}}

) donc l’unité de base pour

ε_0 \: E

est

\mathrm{C.m^{-2}}

. Le moment dipolaire a pour unité de base

\mathrm{C.m}

; par suite, le coefficient de polarisabilité

\displaystyle α=\frac{p}{ε_0 \: E}

a pour unité de base

\mathrm{m^3}

• Le champ subi par la molécule à l’abscisse

x

correspond à :

\displaystyle E_x (x)=\frac{p}{2π \:ε_0 \: x^3}

; donc l’énergie potentielle du dipôle induit dans ce champ est :

\displaystyle ℰ_p=-\overset{→}{E}∙\overset{→}{p}'=-α \:ε_0 \: E_x^{\:2}=-\frac{α \:p^2}{4π^2 \: ε_0 \: x^6}

.
• Finalement, la force subie par la molécule polarisée est :

\displaystyle \overset{→}{F}=-\frac{∂ℰ_p}{∂x} \: \overset{→}{u}_x=-\frac{3 \,α \:p^2}{2π^2 \: ε_0 \: x^7} \: \overset{→}{u}_x

VIII. Force de London

• Sous l'effet d'un champ extérieur

\overset{→}{E}

la molécule acquiert un moment dipolaire

\overset{→}{p}=α \:ε_0 \: \overset{→}{E}

, donc la charge

q

se déplace (relativement) de

\displaystyle \overset{⟶}{OM}=\frac{\overset{→}{p}}{q}=\frac{α \:ε_0 \: \overset{→}{E}}{q}

.
• Si cette charge subit la force extérieure

q \:\overset{→}{E}

, sa nouvelle position d'équilibre indique que son interaction avec

-q

cause alors une force opposée

\displaystyle \overset{→}{F}=-q \:\overset{→}{E}=-\frac{q^2}{α \:ε_0} \: \overset{⟶}{OM}

. Ceci équivaut à l'action d'un ressort de raideur

\displaystyle k=\frac{q^2}{α \:ε_0}

2.	• Pour une molécule isolée, l'équation du mouvement correspond à : $m \:\ddot{x}_1+k \:x_1=0$ . • Les solutions sont de la forme : $x_1=X_1 \: \cos(ω_0 \: t+ϕ)$ avec $\displaystyle ω_0=\sqrt{\frac{k}{m}}$ . Le déplacement moyen $〈x_1 〉$ est donc nul, ainsi que le moment dipolaire moyen.

• Le premier dipôle crée au niveau du second un champ :

\displaystyle E_1=\frac{p_1}{2π \:ε_0 \: x^3}

(algébriquement selon l'axe).
◊ remarque : cela n'apporte rien de plus de détailler que le dipôle est centré en

\displaystyle \frac{x_1}{2}

(ce qui décale

x

) car la correction n'intervient qu'au second ordre (comme ci-après pour

x_2

).

• Le second dipôle subit dans ce champ une force totale qui peut se calculer en ajoutant les forces subies par chaque charge (algébriquement) :

\displaystyle F_{1→2}≈q \: \frac{p_1}{2π \:ε_0 \: x^3}-q \: \frac{p_1}{2π \:ε_0 . (x+x_2 )^3}≈-\frac{3 \:p_1 \: p_2}{2π \:ε_0 \: x^4}

• En ajoutant pour chaque point le champ de l'autre dipôle, les équations des mouvements peuvent s'écrire :

\displaystyle m \:\ddot{x}_2+k \:x_2≈\frac{q^2}{2π \:ε_0 \: x^3} \: x_1

;

\displaystyle m \:\ddot{x}_1+k \:x_1≈\frac{q^2}{2π \:ε_0 \: x^3} \: x_2

.
• Avec

\displaystyle λ=\frac{α}{2π \:x^3}

on peut écrire :

\displaystyle m \:\ddot{x}_2+k \:x_2≈λ\:k \: x_1

\displaystyle m \:\ddot{x}_1+k \:x_1≈λ\:k \: x_2

.
• Les combinaisons indiquées donnent :

m \:\ddot{u}_1+(1-λ) \: k \:u_1≈0

m \:\ddot{u}_2+(1+λ) \: k \:u_2≈0

.
• Ceci correspond à

\displaystyle ω_i=\sqrt{\frac{k_i}{m}}

avec

k_1=(1-λ) \: k

k_2=(1+λ) \: k

.
◊ remarque : de façon générale, lorsque deux systèmes identiques sont mis en interaction, les fréquences propres de l'ensemble se “dédoublent” pour donner une fréquence un peu plus petite et une autre un peu plus grande.

• La force moyenne est :

\displaystyle 〈F_{1→2} 〉=-\frac{3 \:q^2}{2π \:ε_0 \: x^4} \, 〈x_1 x_2 〉=-\frac{3 \,q^2}{8π \:ε_0 \: x^4} \, 〈u_1^{\:2}-u_2^{\:2} 〉

.
• Avec

\displaystyle u_i=\sqrt{\frac{h}{π \:m \:ω_i}} \; \cos(ω_i \: t+β_i )

on obtient :

$\displaystyle 〈F_{1→2} 〉=-\frac{3 \:q^2 \: h}{16π^2 \: ε_0 \: x^4 \: m \:ω_0} \: \left(\frac{1}{\sqrt{1-λ}}-\frac{1}{\sqrt{1+λ}}\right)≈-\frac{3 \,q^2 \: h}{16π^2 \: ε_0 \: x^4 \: m \:ω_0} \, \frac{α}{2π \:x^3}≈-\frac{3 \,α^2 \: h \:ν_0}{16π^2 \: x^7}$ .

IX. Dipôle induit dans un champ extérieur

• Pour étudier les actions respectives exercées par le champ extérieur sur les charges

(

+

)

(

-

)

, on peut les représenter par des charges ponctuelles car elles sont très éloignées des charges qui créent le champ extérieur.
• Au contraire, pour décrire leur interaction, on doit tenir compte (au moins qualitativement) de la répartition de ces charges car leur distance est comparable à la dimension de la zone de répartition.

• En considérant deux charges ponctuelles,

+q

au point

P

-q

au point

N

, dans l'approximation où

P

N

sont très proches en comparaison des autres distances (modèle du dipôle) :

$ℰ_{p_{ext}}=q \:V_{ext} (P)-q \:V_{ext} (N)≈q \:\overset{→}{∇}(V_{ext})∙\overset{⟶}{NP}=-\overset{→}{p}∙\overset{→}{E}$ .

◊ remarque : le champ considéré ici est

\overset{→}{E}=\overset{→}{E}_{ext}

; ce n'est pas le champ total subi par chacune des deux charges puisqu'elles sont en plus en interaction mutuelle.

3.a.	• Pour modéliser le déplacement des charges négatives, on peut ajouter une distribution équivalente de charges positives (qui compensent les anciennes charges négatives) et une distribution de charges négatives dans la nouvelle position. Les charges positives sont alors soumises, en plus du champ préalable dans lequel elles étaient en équilibre, au champ d'une sorte de dipôle. • Puisque le déplacement est faible, l'effet prépondérant subi par les charges positives correspond à “l'intérieur” du dipôle, dans la zone d'intersection des deux distributions. Le théorème de Gauss permet de montrer qu'à l'intérieur d'une distribution sphérique, le champ est $\displaystyle \frac{ρ}{3 \:ε_0} \:\overset{⟶}{PM}$ ou $\displaystyle -\frac{ρ}{3 \:ε_0} \:\overset{⟶}{NM}$ ; le champ total ajouté (celui associé à l'écart à l'équilibre) est donc uniforme : $\displaystyle \overset{→}{E}_{int} (P)≈\frac{ρ}{3 \:ε_0} \: \overset{⟶}{PN}$ .

3.b.	• Avant polarisation, les charges positives et négatives étaient en “équilibre” relatif (moyen, compte tenu du fait que ces charges ne sont pas immobiles). Pour obtenir un nouvel “équilibre”, il faut que le champ supplémentaire total subi par les charges positives soit nul : $\overset{→}{E}+\overset{→}{E}_{int} (P)=\overset{→}{0}$ . ◊ remarque : ceci suppose aussi que le déplacement soit faible.

3.c.	• Le moment dipolaire induit est $\overset{→}{p}=q \:\overset{⟶}{NP}$ où $q$ est proportionnel à $ρ$ (avec une constante dépendant de la géométrie précise) et donc proportionnel à $\overset{→}{E}$ .

3.d.	• La force de rappel proportionnelle à l'écartement des charges peut être décrite par un ressort tel que : $k \:\overset{⟶}{PN}=q \:\overset{→}{E}_{int} (P)$ . Ceci correspond à : $\displaystyle k \:\overset{⟶}{NP}=q \:\overset{→}{E}=\frac{q}{α \:ε_0} \: \overset{→}{p}$ donc $\displaystyle k=\frac{q^2}{α \:ε_0}$ .

3.e.	• L'énergie potentielle “interne” décrivant la polarisation (en prenant comme référence la molécule non polarisée) peut s'écrire : $\displaystyle ℰ_{p_{int}}=\frac{1}{2} k \;\overset{⟶}{NP}^{2}=\frac{p^2}{2 \,α \:ε_0}=\frac{1}{2} \,\overset{→}{p}∙\overset{→}{E}$ .

4.	• En prenant en compte toutes les interactions, on obtient finalement : $ℰ_p=ℰ_{p_{ext}}+ℰ_{p_{int}}=-\frac{1}{2} \, \overset{→}{p}∙\overset{→}{E}$ .

X. Dipôle quelconque dans un champ extérieur

• La force peut s'écrire :

\overset{→}{F}=q \:\overset{→}{E}(P)-q \:\overset{→}{E}(N)

.
• En utilisant un repère local avec une coordonnée

ξ

orientée selon le dipôle :

\displaystyle \overset{→}{F}=p \, \frac{d\overset{→}{E}}{dξ}

.
• Avec des notations plus générales, cette “dérivée selon

\overset{→}{p}

” peut s'écrire :

\overset{→}{F}=\left(\overset{→}{p}∙\overset{→}{∇}\,\right) \, \overset{→}{E}

2.a.	• On peut écrire : $\overset{→}{F}=\left(\overset{→}{p}_0∙\overset{→}{∇}\,\right) \, \overset{→}{E}+α \:ε_0 .\left(\overset{→}{E}∙\overset{→}{∇} \,\right) \, \overset{→}{E}$ . • La partie associée au moment dipolaire permanent (polarisation) est : $\left(\overset{→}{p}_0∙\overset{→}{∇} \,\right) \, \overset{→}{E}=\overset{→}{∇}\left(\overset{→}{p}_0∙\overset{→}{E} \,\right)$ correspondant à une énergie potentielle “externe” : $ℰ_{p_{ext}}=-\overset{→}{p}_0∙\overset{→}{E}$ . • La partie associée au moment dipolaire induit (polarisabilité) est : $\displaystyle α \:ε_0 .\left(\overset{→}{E}∙\overset{→}{∇} \,\right) \, \overset{→}{E}=α \:ε_0 \: \overset{→}{∇}\left(\frac{\overset{→}{E}^2}{2}\right)$ car $\displaystyle \overset{→}{∇} × \overset{→}{E}=-\frac{∂\overset{→}{B}}{∂t}=\overset{→}{0}$ en l'absence de phénomènes magnétiques variables ; ceci correspond à une énergie potentielle “interne” : $ℰ_{p_{int}}=-\frac{1}{2} α \:ε_0 \: \overset{→}{E}^2=-\frac{1}{2} \, \overset{→}{p}_{ind}∙\overset{→}{E}$ . ◊ remarque : en toute rigueur, un déplacement de dipôle correspond à un déplacement de charges, dont à des courants, donc à des effets magnétiques induits ; toutefois, non seulement ceux-ci sont a priori du second ordre, mais ils sont de plus d'autant plus négligeables que les variations sont lentes ; on peut ici les considérer nuls. • Au total : $ℰ_p=-\overset{→}{p}_0∙\overset{→}{E}-\frac{1}{2} α \:ε_0 \, \overset{→}{E}^2=-\overset{→}{p}∙\overset{→}{E}+\frac{1}{2} α \:ε_0 \, \overset{→}{E}^2$ (énergie du dipôle orienté modifiée par l'énergie nécessaire pour créer la partie due à la polarisabilité).

2.b.	• Étant donné que l'expression de l'énergie potentielle fait intervenir les parties $\overset{→}{p}_0$ et $α \:ε_0 \: \overset{→}{E}$ avec des coefficients différents, on ne peut pas trouver d'expression en fonction de seulement $\overset{→}{p}$ et $\overset{→}{E}$ (il faut au moins faire intervenir $α$ dont dépend la proportion du moment dipolaire qui est induit).