DIPÔLE ÉLECTROSTATIQUE - exercices


A. EXERCICES DE BASE

I. Lignes de champ

        • On considère le champ E→\overset{→}{E} défini dans un plan par ses composantes en coordonnées polaires :

 Er=2kcos(θ)r3\displaystyle E_r=2 \,k \: \frac{\cos(θ)}{r^3}   et   Eθ=ksin(θ)r3\displaystyle E_θ=k \: \frac{\sin(θ)}{r^3}   (où kk est une constante).

1.     • Trouver l'équation des lignes de champ.

2.     • Montrer que ce champ dérive d'un potentiel VV ,  puis déterminer ce potentiel sachant que  V→0V→0  quand  r→∞r→∞ .


II. Champ et flux

        • On considère un champ vectoriel à symétrie de révolution autour de l'axe OzOz ; on l'étudie dans un plan méridien (c'est-à-dire un plan contenant OzOz ). Dans ce plan, on adopte les coordonnées polaires avec OzOz comme axe polaire.

        • Le champ vectoriel dérive d'un potentiel  V=k3cos2(θ)−1r3\displaystyle V=k \: \frac{3 \,\cos^2(θ)-1}{r^3}  où kk est une constante.

1.     • Quelle est l'allure des courbes équipotentielles ?

2.     • Déterminer les coordonnées du champ  E→=−∇→V\overset{→}{E}=-\overset{→}{∇} V .

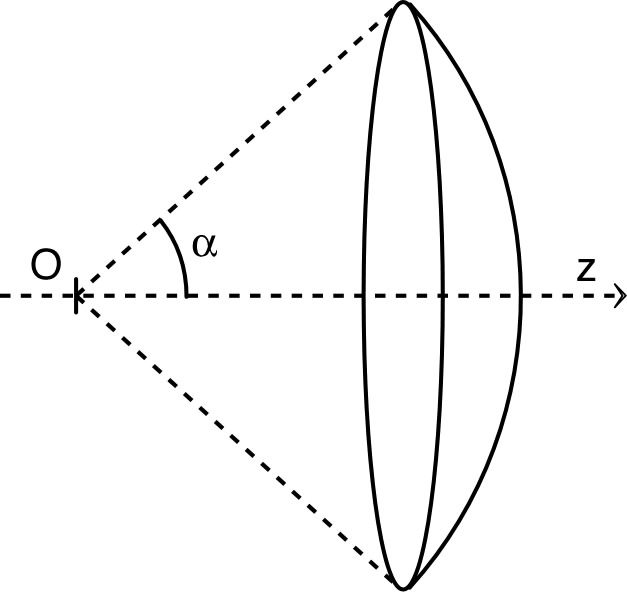
3.     • Calculer le flux de ce champ à travers une calotte sphérique centrée en OO ,  de révolution autour de OzOz (choisi “horizontal” sur le schéma ci-contre) et “vue” depuis OO sous un angle  2α2 \,α .
        • Considérer ensuite les cas particuliers  α=π2α=\frac{π}{2}  et  α=πα=π .
dipoleElStat_ex_Im/dipoleElStat_ex_Im1.jpg


III. Tracé d'un diagramme électrique

        • Trois charges égales (qq) sont placées aux sommets d'un triangle équilatéral ABCABC ; on désigne par GG le centre de ce triangle et on pose :  a=AGa=AG (le triangle a donc pour côté  a3a \:\sqrt{3} ).

1.     • Tracer rapidement (sans calcul approfondi), dans le plan de ABCABC , l'allure des lignes équipotentielles et des lignes de champ électrostatiques.

2.     • Calculer le potentiel en un point MM de la droite définie par GAGA (on pose pour cela  y=GM¯y=\widebar{GM} ,   distance algébrique comptée positivement dans de sens de GG vers AA ). Montrer qu'il y a quatre points où le champ est nul ; déterminer leur position, au moins approximativement (en faisant un développement de V(y)V(y) au troisième ordre par rapport à ya\displaystyle \frac{y}{a} ).


IV. Répartition surfacique de dipôles

        • Un disque de rayon RR est tapissé de dipôles, de sorte que la densité de moment dipolaire  μ=dpdS\displaystyle μ=\frac{dp}{dS}  soit une constante. La direction des dipôles est normale au plan du disque. Calculer le champ et le potentiel électrostatiques sur l'axe, à la distance xx du centre du disque.


V. Dipôle cylindrique

        • Deux fils identiques, cylindriques de rayon  aa  très petit, “infiniment” longs, sont disposés dans le vide parallèlement à l'axe OzOz aux abscisses  x=±d2\displaystyle x=±\frac{d}{2}  avec  d≫a d≫a .  Le fil (1)(1), situé à  x=d2\displaystyle x=\frac{d}{2}  porte la densité linéique de charge  λ>0λ>0 ; l'autre (2)(2) porte la densité linéique de charge −λ-λ .

1.     a) Justifier que dans ce cas le modèle théorique du fil rectiligne “infini” peut donner une représentation acceptable, par compensation des effets axiaux pour des charges opposées portées par les deux fils.
        b) Calculer le potentiel électrostatique V(r1,r2)V(r_1 \, , \,r_2) en un point MM situé à une distance r1r_1 du fil (1)(1) et à la distance r2r_2 du fil (2)(2) ; prendre pour référence  V=0V=0  sur OzOz .

2.     • Si on fait tendre dd vers zéro, mais en gardant constant le produit  p=λdp=λ \:d ,  on obtient un “dipôle cylindrique” de moment dipolaire p→\overset{→}{p} (orienté selon OxOx ). Calculer le potentiel V(r,θ)V(r,θ) en MM . En déduire les composantes ErE_r et EθE_θ du champ électrostatique E→\overset{→}{E} en MM .


B. EXERCICES D’APPROFONDISSEMENT

VI. Force de Keesom

        • On considère deux dipôles permanents, dont les moments p→0\overset{→}{p}_0 et p→0′\overset{→}{p}'_0 sont portés par l'axe OxOx ,  placés à la distance rr l'un de l'autre. Pour simplifier, on fait l'hypothèse restrictive qu'il n'y a que deux orientations relatives possibles : avec les moments dipolaires “parallèles” (sous-entendu : de même sens) ou “antiparallèles” (c'est-à-dire parallèles et de sens contraires).

1.     • Calculer dans les deux cas la force qui s'exerce entre les dipôles.

2.     • Le travail élémentaire d'un couple de forces de moment algébrique ℳℳ est :  dW=ℳdθdW=ℳ \:dθ  où dθdθ désigne l'angle algébrique de rotation élémentaire (avec le même axe que ℳℳ ). Montrer de façon générale que, si un dipôle permanent est placé dans un champ électrique E→\overset{→}{E} ,  avec son moment dipolaire p→\overset{→}{p} parallèle au champ (et sous-entendu : de même sens), il faut lui fournir un travail  W=2pEW=2 \,p \:E  pour le retourner dans la position “anti-parallèle” (parallèle et de sens contraire).

3.     • On suppose que l'agitation thermique est assez forte pour faire passer sans cesse les dipôles de la question (1) d'une position à l'autre. Expliciter la condition correspondante et calculer la force moyenne qui s'exerce alors entre les deux dipôles (on peut supposer  W≪kTW≪k \:T ).
        ◊ rappel : le facteur de Boltzmann prévoit une répartition statistique :  n=n0e−W/kTn=n_0 \: \mathrm{e}^{-W/kT}  avec la constante de Boltzmann  k=RNA\displaystyle k=\frac{R}{N_{\mathrm{A}}}   et où n0n_0 est une constante de normalisation.


VII. Force de Debye

1.     • Justifier l'unité du coefficient de polarisabilité  αα  et son ordre de grandeur usuel   α≈10−30m3α≈{10}^{-30} \: \mathrm{m^3} .

2.     • Un dipôle permanent placé en OO a son moment dipolaire p→\overset{→}{p} orienté selon OxOx . À l'abscisse xx se trouve une molécule polarisable qui, sous l'effet du champ électrostatique E→\overset{→}{E} créé par le dipôle, acquiert un moment dipolaire  p→′=αε0E→\overset{→}{p}'=α \:ε_0 \: \overset{→}{E} .   Calculer la force qui s'exerce alors entre le dipôle permanent et le dipôle induit.


VIII. Force de London

        • On considère des molécules symétriques ; le barycentre des charges positives coïncide avec celui des charges négatives. Sous l'action d'un champ E→\overset{→}{E} les molécules peuvent par contre se polariser et acquérir un moment dipolaire induit  p→=αε0E→\overset{→}{p}=α \:ε_0 \: \overset{→}{E} .

1.     • Montrer qu'on peut représenter cette molécule par une charge fixe −q-q en OO et une charge mobile +q+q en MM “rappelée” vers OO par une force   f→=−kOM⟶\overset{→}{f}=-k \:\overset{⟶}{OM}  ; calculer la “raideur” kk en fonction de αα , ε0ε_0 et qq .

2.     • On considère une (seule) molécule représentée comme précédemment par deux charges en O1O_1 et M1M_1 donc possédant un moment dipolaire  p→1=qO1M1→\overset{→}{p}_1=q \;\overset{→}{O_1 M_1} .  Écrire l'équation du mouvement de M1M_1 et montrer que la valeur moyenne (dans le temps) de p→1\overset{→}{p}_1 est nulle.

3.     • On considère une seconde molécule, identique à la première, représentée par deux charges en O2O_2 et M2M_2 . Pour simplifier, on suppose l'ensemble aligné selon l'axe OxOx .
        • On pose :  O1O2=xO_1 O_2=x ,  O1M1=x1O_1 M_1=x_1  et  O2M2=x2O_2 M_2=x_2  ;  on suppose que  x1x_1 et x2≪xx_2≪x .  Exprimer, en fonction de p1p_1 , p2p_2 et xx ,  la force qui s'exerce entre ces deux dipôles.

4.     • Écrire les équations du mouvement de M1M_1 et M2M_2 (en tenant compte du fait que  x1x_1 et x2≪xx_2≪x ).
        • On pose  u1=x1+x2u_1=x_1+x_2  et  u2=x1−x2u_2=x_1-x_2  ;  montrer que u1u_1 et u2u_2 peuvent s'écrire sous la forme :  ui=Aicos(ωit+βi)u_i=A_i \: \cos(ω_i \: t+β_i)  et expliciter ω1ω_1 et ω2ω_2 (on peut pour cela expliciter les raideurs kik_i en fonction de αα et poser  λ=α2πx3≪1\displaystyle λ=\frac{α}{2π \:x^3}≪1 ).

5.     • La mécanique quantique montre que  Ai=hπmωi\displaystyle A_i=\sqrt{\frac{h}{π \:m \:ω_i}}  où hh est la constante de Planck (ceci se retrouve “qualitativement” avec les incertitudes de Heisenberg). Calculer la force moyenne qui s'exerce entre les deux dipôles (moyenne dans le temps en supposant O1O_1 et O2O_2 fixes). Expliciter cette force en fonction de αα , hh , xx  et la fréquence  ν0=12πkm\displaystyle ν_0=\frac{1}{2π} \, \sqrt{\frac{k}{m}} .


IX. Dipôle induit dans un champ extérieur

1.     • On considère une molécule symétrique ; le barycentre des charges positives coïncide avec celui des charges négatives. Sous l'action d'un champ E→\overset{→}{E} cette molécule peut se polariser et acquérir un moment dipolaire induit  p→=αε0E→\overset{→}{p}=α \:ε_0 \: \overset{→}{E} .
        • Pour modéliser ce phénomène, justifier qu'on peut étudier les actions respectives exercées par le champ extérieur sur les charges (++) et (−-) en les représentant par des charges ponctuelles, mais qu'on doit tenir compte (au moins qualitativement) de la répartition de ces charges pour décrire leur interaction.
        ◊ remarque : même pour un atome dont le noyau et les électrons sont quasi-ponctuels, le mouvement de ces derniers les fait apparaître comme des charges “réparties” dans l'espace.

2.     • Exprimer l'énergie potentielle “externe” ℰpextℰ_{p_{ext}} décrivant le dipôle p→\overset{→}{p} par rapport au champ extérieur en le considérant comme un dipôle “rigide” (polarisé de façon permanente et non polarisable).

3.     • Pour modéliser qualitativement la polarisabilité, on veut commencer par décrire l'interaction des deux charges compte tenu de leur répartition. On simplifie en considérant deux répartitions sphériques de densités volumiques  ±ρ±ρ  uniformes, initialement superposées et en équilibre. dipoleElStat_ex_Im/dipoleElStat_ex_Im2.jpg
        a) Montrer qu'un décalage global PN⟶\overset{⟶}{PN} des charges négatives peut être décrit, dans la zone concernée, par l'ajout d'un champ “intérieur”  E→int(P)≈ρ3ε0PN⟶\displaystyle \overset{→}{E}_{int} (P)≈\frac{ρ}{3 \,ε_0} \,\overset{⟶}{PN}  subi par les charges positives.
        b) Sous l'effet du champ extérieur E→\overset{→}{E} , la molécule se polarise d'une façon que les charges soient “en moyenne” en équilibre. En déduire le bilan des champs subis par les charges positives.
        c) Retrouver ainsi que le moment dipolaire induit peut s'écrire sous la forme  p→=αε0E→\overset{→}{p}=α \:ε_0 \: \overset{→}{E}  où αα est une constante dépendant de la répartition précise des charges (“justifiant” donc l'expression classique de p→\overset{→}{p} induit).
        d) En déduire que, lors de la polarisation, l'interaction des charges positives et négatives peut être décrite par un “ressort équivalent” ; calculer la raideur kk correspondante.
        e) Exprimer l'énergie potentielle “interne” ℰpintℰ_{p_{int}} décrivant la polarisation (en prenant comme référence la molécule non polarisée).

4.     • Conclure en exprimant l'énergie potentielle ℰpℰ_p décrivant le dipôle p→\overset{→}{p} par rapport au champ extérieur (compte tenu du fait qu'il apparaît par effet de polarisabilité).


X. Dipôle quelconque dans un champ extérieur

1.     • On considère une molécule polarisée ; le barycentre des charges positives ne coïncide pas avec celui des charges négatives : il existe donc un moment dipolaire p→0\overset{→}{p}_0 . Sous l'action d'un champ E→\overset{→}{E} cette molécule est de plus polarisable : elle peut acquérir un moment dipolaire induit tel que :  p→=p→0+αε0E→\overset{→}{p}=\overset{→}{p}_0+α \:ε_0 \: \overset{→}{E} .
        • Pour étudier l'interaction avec le champ extérieur, on modélise ce dipôle par deux charges ponctuelles (positive et négative). Établir l'expression de la force subie par ce dipôle, placé dans un champ extérieur quelconque (non nécessairement uniforme).

2.     a) Montrer que cette force dérive d'une énergie potentielle (et exprimer celle-ci).
        b) Est-il possible d'exprimer cette énergie potentielle en fonction uniquement de p→\overset{→}{p} et E→\overset{→}{E} ?
       ☞ indications : propriété mathématique :  (E→⋅∇→)E→=∇→(E→22)+(∇→×E→)×E→(\overset{→}{E}⋅\overset{→}{∇} \,) \,\overset{→}{E}=\overset{→}{∇}\left(\frac{\overset{→}{E}^2}{2}\right)+(\overset{→}{∇} × \overset{→}{E} \,) × \overset{→}{E}  ;
propriété électromagnétique :  ∇→×E→=−∂B→∂t\displaystyle \overset{→}{∇} × \overset{→}{E}=-\frac{∂\overset{→}{B}}{∂t} .