| . |
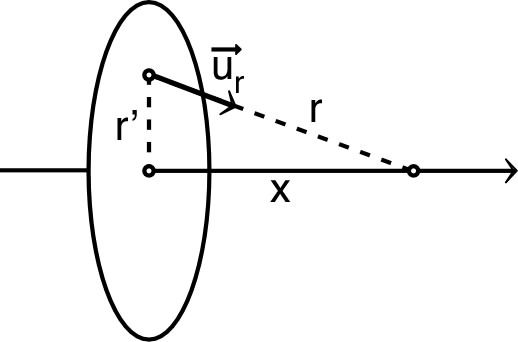
Par symétrie car, perpendiculairement à l’axe, les contributions des charges symétriques se compensent. On considère donc : .
Il est alors pratique de décrire la
“concentration” des charges élémentaires par une densité de
charge :
|
| • L’interaction électrostatique entre deux charges en et (dans le vide) est décrite par la loi de Coulomb : , avec , et ( ). |
| La quantité : décrit donc une propriété de l’espace en , provoquée par l’action de ; cette quantité (vectorielle) est appelée “champ électrostatique” (au point ). |
Par symétrie car, perpendiculairement à l’axe, les contributions des charges symétriques se compensent. On considère donc : . |
 |
• La somme des vecteurs étant compliquée, on
peut utiliser une autre description, équivalente, car
dérive d’un potentiel tel
que :
Inversement, la différence de potentiel entre deux points et se calcule par la “circulation” du champ électrostatique sur un trajet quelconque de à :
|
|
en coordonnées cylindriques ; en coordonnées sphériques. |
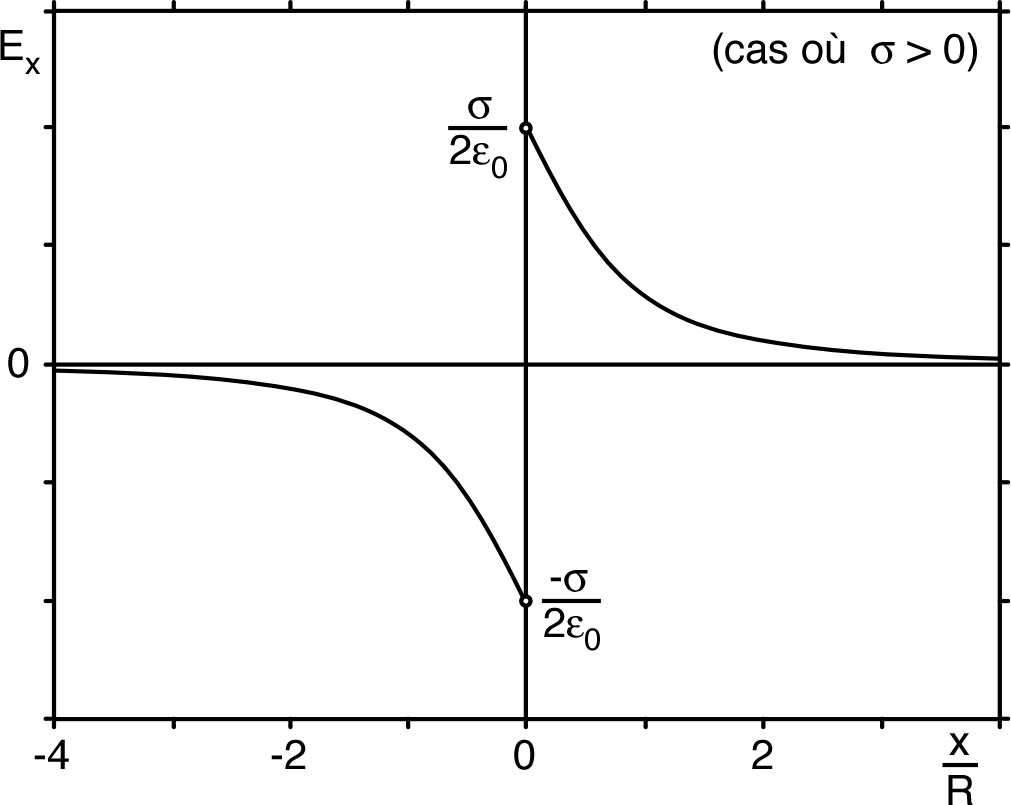
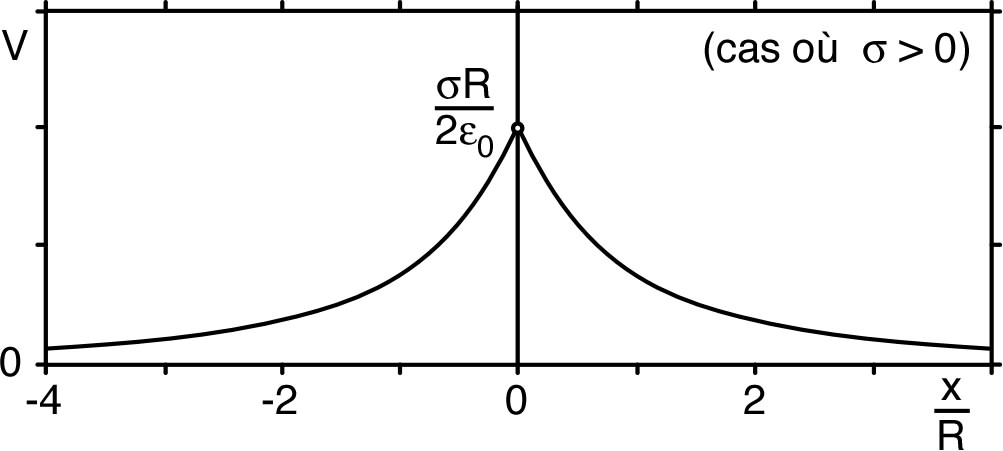
| • Pour une charge ponctuelle, on obtient : (où on choisit généralement ), correspondant à : (champ radial), avec : . |
| (où on choisit généralement ). |
| avec . |