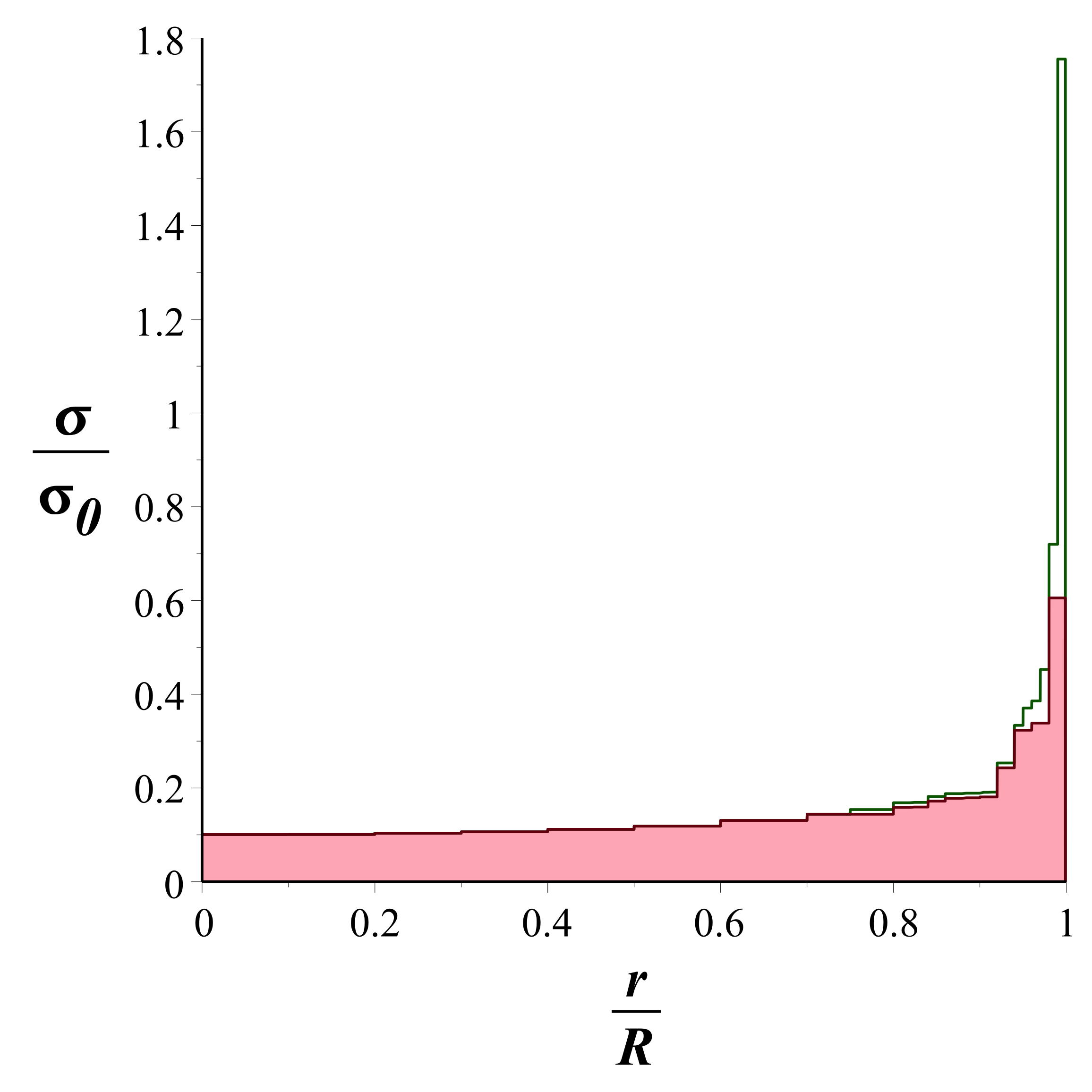
| 1.a. |
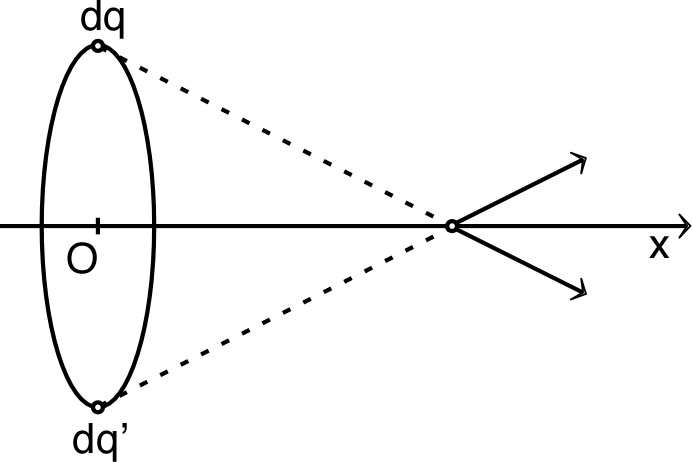
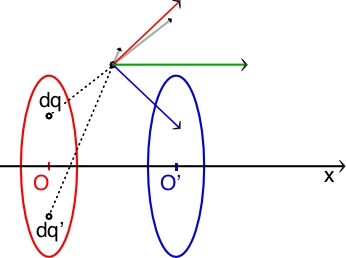
• Pour tout point hors
de l'axe
,
le point et
l'axe déterminent un plan . La
répartition des charges est symétrique par rapport à ce
plan. Le champ en doit
donc être invariant dans cette symétrie, donc parallèle à ce
plan :
.
• Par ailleurs, la répartition de
charge est invariante dans une rotation
d'angle
selon l'axe
,
donc dans cette transformation le champ
doit simplement tourner comme le point
. Ceci impose que
et
ne dépendent pas de
(l'effet de la rotation se limite à la rotation
de
).
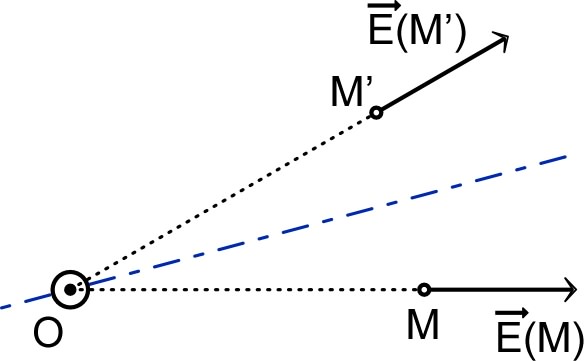
◊ remarque : soit
le point déduit de
dans une rotation d'axe
et d'angle
, on peut aussi comparer
et
qui doivent être symétriques par rapport au plan
bissecteur (le schéma ci-contre n'indique qu'un
exemple ; le sens des vecteurs dépend des cas). |
|
|
|
| 1.b. |
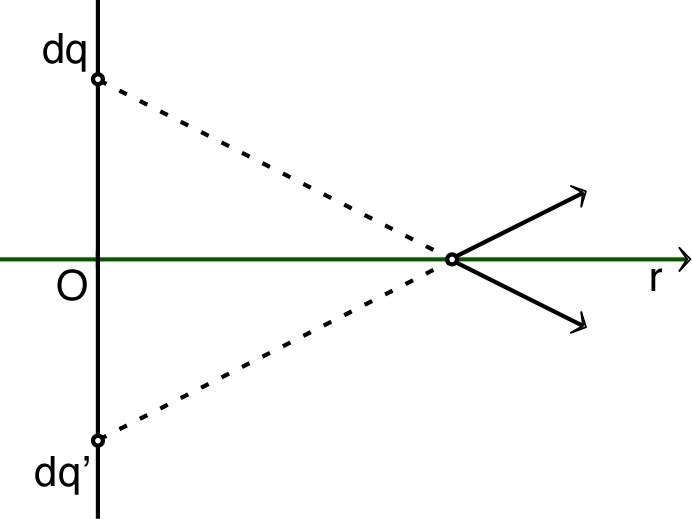
• La difficulté pour calculer en coordonnées
polaires tient au fait que
(angle )
portant des charges n'est en général pas dans le plan défini
par et
l'axe
,
choisi comme origine des angles.
• On peut utiliser des coordonnées intermédiaires
cartésiennes
vers le haut et
vers l'avant :
;
. Ceci permet de calculer
et
puis d'intégrer les charges sur
:
. |