CHAMP ÉLECTROSTATIQUE - exercices


A. EXERCICES DE BASE

I. Répartition volumique de charges

        • Une boule BB de centre OO et de rayon R est chargée d’une densité volumique ne dépendant que de la distance au centre rr :  ρ(r)=ρ0.(1−ar2R2)\displaystyle ρ(r)=ρ_0 .\left(1-a \,\frac{r^2}{R^2} \right)  où  ρ0ρ_0  et  aa  sont deux constantes.

1.     a) Quelle est la charge infinitésimale dQdQ comprise entre deux sphères centrées en OO et dont les rayons sont  rr  et   r+drr+dr ?
        b) Quelle est la charge totale QQ portée par la boule ?

2.     a) Quelle est la charge volumique moyenne  ρm=Q𝒱\displaystyle ρ_m=\frac{Q}{𝒱}  ?
        b) Pourquoi ρmρ_m est-elle différente de la moyenne :  1R∫0Rρ(r)dr\displaystyle \frac{1}{R} \:∫_0^R ρ(r) \: dr  ?


II. Électrisation d'une boule

        • Deux boules, en cuivre, de même rayon  R=2mmR=2 \:\mathrm{mm} ,  sont placées à la distance  d=5cmd=5 \:\mathrm{cm}  l'une de l'autre (d≫Rd≫R ). Elles portent toutes deux la même charge QQ positive.

1.     • Calculer QQ sachant que la force répulsive entre les deux boules a pour norme  F=0,2NF=\text{0,2} \:\mathrm{N} .

2.     • Calculer le nombre N1N_1 d'électrons perdus par chaque boule lors de l’électrisation.

3.     • Comparer N1N_1 au nombre N0N_0 d'atomes de cuivre dans chaque boule sachant que la masse volumique du cuivre est  μ=8,9.103kg.m−3μ=\text{8,9}.{10}^3 \: \mathrm{kg.m^{-3}}  et que sa masse molaire est  M=63,54g.mol−1M=\text{63,54} \:\mathrm{g.mol^{-1}} .

4.     • En pratique, les charges se répartissent en surface. Comparer N1N_1 au nombre N0′N'_0 d'atomes de cuivre dans la couche chargée en supposant son épaisseur de l'ordre de grandeur du diamètre des atomes, dont le rayon est  r=128pmr=128 \:\mathrm{pm} .

5.     • Quelle force F′F' s'exercerait entre les deux boules si elles étaient électrisées avec  N1=N0N_1=N_0 ?

Données :  charge de l'électron :  qe=−1,6.10−19Cq_e=-\text{1,6}.{10}^{-19} \: \mathrm{C}  ;  nombre d'Avogadro :  NA=6,02.1023N_A=\text{6,02}.{10}^{23} .


III. Loi de Coulomb

        • Un anneau fin, de centre OO et de rayon RR ,  porte la charge QQ répartie régulièrement sur sa circonférence. Une charge qq est mobile sur l'axe OxOx perpendiculaire en OO au plan de l'anneau. Calculer, en fonction de xx ,  la force qui s'exerce sur la charge qq .


IV. Champ d'un segment chargé

1.     • On considère un fil rectiligne de longueur LL , comportant une charge linéique (ou densité linéique de charge) notée λλ .
        • Pour étudier le champ électrique créé par ce fil, on utilise un repère cylindrique dont l'origine est au milieu du fil et dont l'axe (Oz)(Oz) est dans la direction du fil. Avec ces notations, la charge linéique peut s'écrire sous la forme :  λ=λ0.(1+αz2L2)\displaystyle λ=λ_0 .\left(1+α \:\frac{z^2}{L^2} \right)  où λ0λ_0 et αα sont deux constantes.
        a) Soit  M(r,θ,z)M(r,θ,z)  un point quelconque de l'espace, hors du fil, montrer que le champ électrique en ce point peut s'écrire :  E→(M)=Er(r,z)u→r+Ez(r,z)u→z\overset{→}{E}(M)=E_r (r,z)\: \overset{→}{u}_r+E_z (r,z)\: \overset{→}{u}_z  (en justifiant clairement le raisonnement utilisé).
        b) Écrire l'expression intégrale du champ, déduite de la loi de Coulomb (il n'est pas demandé de calculer l'intégrale).

2.     • On se limite maintenant aux points MM du plan d'équation  z=0z=0 .
        a) Montrer que le champ électrique en ce point peut s'écrire :  E→(M)=Er(r)u→r\overset{→}{E}(M)=E_r (r) \:\overset{→}{u}_r .
        b) En déduire l'expression intégrale de la composante algébrique Er(r)E_r (r) .
        c) Calculer cette intégrale.


V. Champ d'un disque chargé

1.     • On considère un disque de rayon RR , comportant une charge surfacique (ou densité surfacique de charge) notée σσ .
        • Pour étudier le champ électrique créé par ce disque, on utilise un repère cylindrique dont l'origine est au milieu du disque et dont l'axe (Ox)(Ox) est perpendiculaire au disque. Avec ces notations, la charge surfacique peut s'écrire sous la forme :  σ=σ0.(1−2r′R)\displaystyle σ=σ_0 .\left(1-\frac{2 \, r'}{R\:}\right)  où σ0σ_0 est une constante.
        a) Soit  M(r,θ,x)M(r,θ,x)  un point quelconque de l'espace, hors du disque, montrer (en justifiant clairement le raisonnement utilisé) que le champ électrique en ce point peut s'écrire :  E→(M)=Er(r,x)u→r+Ex(r,x)u→x\overset{→}{E}(M)=E_r (r,x) \:\overset{→}{u}_r+E_x (r,x) \:\overset{→}{u}_x .
        b) Écrire l'expression intégrale du champ, déduite de la loi de Coulomb (il n'est pas demandé de calculer l'intégrale).
elecStatique_ex_im/elecStatique_ex_im3.jpg

2.     • On se limite maintenant aux points MM de l'axe (Ox)(Ox), c'est à dire tels que  r=0r=0 .
        a) Montrer que le champ électrique en ce point peut s'écrire :  E→(M)=Ex(x)u→x\overset{→}{E}(M)=E_x (x) \:\overset{→}{u}_x .
        b) En déduire l'expression intégrale de la composante algébrique Ex(x)E_x (x) .
        c) Calculer cette intégrale.


VI. Gradient par rapport aux coordonnées d'un point

        • On considère une grandeur physique scalaire  V(M1;M2)V(M_1 ; M_2)  fonction de deux points M1M_1 et M2M_2 , mais ne dépendant en fait que de la distance  r=M1M2r=M_1 M_2 .  On peut alors noter V(r)V(r) l'expression correspondante.
        • Exprimer  ∇→1V\overset{→}{∇}_1 V  en fonction de  dVdr\displaystyle \frac{dV}{dr}  (l'indice 1 signifie que les dérivées du gradient doivent s'appliquer aux coordonnées (x1,y1,z1)(x_1 ,y_1 ,z_1) de M1M_1 ).
        • Comparer avec  ∇→2V\overset{→}{∇}_2 V .


VII. Champ d'un segment uniformément chargé

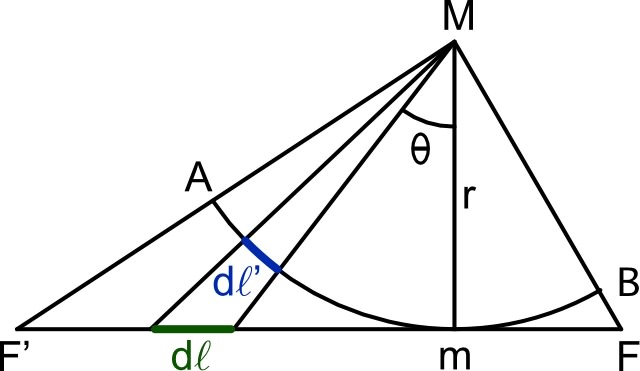
        • On considère un segment  F′FF'F  uniformément chargé d'une densité linéique λλ . On étudie le champ et le potentiel en un point MM situé à la distance  r=mMr=mM  du segment.

1.     • On considère alors, dans le plan MF′FMF'F , un arc de cercle AmB⌢\overset{\frown}{AmB} de centre MM , tangent en mm à  F′FF'F  et portant la même densité de charge λλ .
elecStatique_ex_im/elecStatique_ex_im1.jpg

        • Montrer que les éléments infinitésimaux d𝓁d𝓁 (du segment F′FF'F ) et d𝓁′d𝓁' (de l'arc AmB⌢\overset{\frown}{AmB} ), “vus” du point MM sous le même angle dθdθ , créent en MM le même champ élémentaire.

2.     • Déduire du résultat précédent la direction du champ créé par la ligne ABAB au point MM . Montrer que les surfaces équipotentielles sont des ellipsoïdes de révolution de foyers F′F' et FF .
        ◊ remarque : on rappelle que la normale en un point à une ellipse est la bissectrice de l'angle qui joint ce point aux deux foyers.

3.     • Calculer la valeur du potentiel sur une des équipotentielles, en posant  F′F=2cF'F=2 \,c ,  Q=2cλQ=2 \,c \,λ  et en désignant par  aa  le demi-grand axe de l'ellipsoïde considéré.


VIII. Identité de Gauss

        • On considère un ensemble de nn points fixes AiA_i . Dans un premier état, on place des charges ponctuelles qiq_i aux points AiA_i et on désigne par ViV_i les potentiels respectifs aux points AiA_i (le potentiel en un point AiA_i est créé par l'action des charges autres que qiq_i ). Dans un second état, on place aux mêmes points AiA_i d'autres charges ponctuelles qi′q'_i et on désigne par Vi′V'_i les nouveaux potentiels respectifs aux points AiA_i .
        • Montrer que :   ∑qiVi′=∑qi′Vi\displaystyle ∑ \,q_i \:V'_i =∑ \,q'_i \:V_i   (identité de Gauss).


B. EXERCICES D'APPROFONDISSEMENT

IX. Champ d'un disque chargé

1.     • On considère un disque de rayon RR , comportant une charge surfacique (ou densité surfacique de charge) uniforme notée σσ .
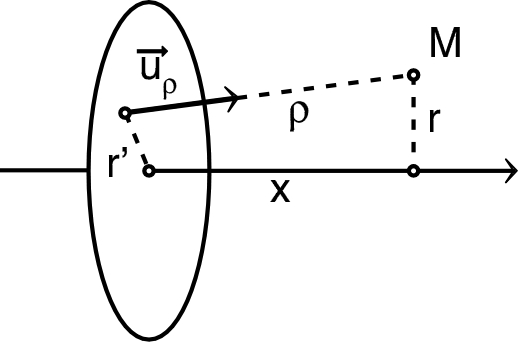
        • Pour étudier le champ électrique créé par ce disque, on utilise un repère cylindrique dont l'origine est au milieu du disque et dont l'axe (Ox)(Ox) est perpendiculaire au disque.
        a) Soit  M(r,θ,x)M(r,θ,x)  un point quelconque de l'espace, hors du disque, montrer (en justifiant clairement le raisonnement utilisé) que le champ électrique en ce point peut s'écrire :  E→(M)=Er(r,x)u→r+Ex(r,x)u→x\overset{→}{E}(M)=E_r (r,x) \:\overset{→}{u}_r+E_x (r,x) \:\overset{→}{u}_x .
        b) Écrire les expressions intégrales du champ et de ses composantes, selon la loi de Coulomb (il n'est pas demandé de calculer les intégrales.
elecStatique_ex_im/elecStatique_ex_im3.jpg

2.     • On se propose d'étudier les propriétés du champ au moyen du calcul numérique des intégrales.
        a) Déterminer graphiquement Ex(r,x)E_x (r,x) pour respectivement  xR=0,05;0,02;0,01\displaystyle \frac{x}{R}=\text{0,05} \:; \text{0,02} \:; \text{0,01} .  Commenter.
        b) Déterminer graphiquement Er(r,x)E_r (r,x) pour respectivement  xR=0,05;0,02;0,01\displaystyle \frac{x}{R}=\text{0,05} \:; \text{0,02} \:; \text{0,01} .  Commenter.

3.     • En déduire les propriétés générales du champ dans la zone entre deux plaques analogues parallèles portant des charges opposées. Commenter.


X. Champ d'un disque chargé

1.     • On considère un disque de rayon RR , comportant une charge surfacique (ou densité surfacique de charge) uniforme notée σσ .
        • Pour étudier la répartition des charges et le potentiel créé par ce disque, on utilise un repère cylindrique dont l'origine est au milieu du disque et dont l'axe (Ox)(Ox) est perpendiculaire au disque.
        a) Justifier qualitativement que la répartition ne peut pas être uniforme et préciser la façon dont elle dépend du point PP sur le disque.
        b) Soit  M(r,θ,x)M(r,θ,x)  un point quelconque de l'espace, hors du disque, montrer (en justifiant clairement le raisonnement utilisé) que le potentiel en ce point peut s'écrire  V(r,x)V(r,x) .
elecStatique_ex_im/elecStatique_ex_im3.jpg
        c) Écrire l'expression intégrale du potentiel selon la loi de Coulomb (il n'est pas demandé de calculer l'intégrale) ; préciser le cas particulier en surface du disque  (x=0x=0 ).

2.     • On se propose d'étudier les propriétés du potentiel au moyen du calcul numérique des intégrales. On développe pour cela en une série de la forme  σ(r)=c0+c1r+c2r2+c3r3+c4r4+⋯σ(r)=c_0+c_1 \:r+c_2 \:r^2+c_3 \:r^3+c_4 \:r^4 +⋯ .
        a) Préciser les intégrales ℐn(r)ℐ_n (r) à calculer pour obtenir un développement analogue :

 V(r)=c0ℐ0(r)+c1ℐ1(r)+c2ℐ2(r)+c3ℐ3(r)+⋯V(r)=c_0 \: ℐ_0 (r) + c_1 \:ℐ_1 (r) + c_2 \:ℐ_2 (r) + c_3 \:ℐ_3 (r) + ⋯ .
        b) Déterminer numériquement les fonctions ℐn(r)ℐ_n (r) puis ajuster les coefficients cnc_n donnant  V=CsteV=Cste .
        c) En déduire une représentation graphique de σ(r)σ(r) ; commenter.

3.     • Une autre approche consiste à découper l'intervalle  [0;R]\left[0 \,;R\right]  par une suite de valeurs rkr_k avec  r0=0r_0=0   et  RN=RR_N=R ,  puis à développer en une série de la forme  σ(r)=c0+c1H(r−r1)+c2H(r−r2)+⋯σ(r)=c_0+c_1 \:\mathrm{H}(r-r_1)+c_2 \:\mathrm{H}(r-r_2) +⋯  (fonction en escalier) où H\mathrm{H} désigne la fonction échelon de Heaviside.
        a) Préciser les intégrales 𝒥n(r)𝒥_n (r) à calculer pour obtenir un développement analogue :

 V(r)=c0𝒥0(r)+c1𝒥1(r)+c2𝒥2(r)+c3𝒥3(r)+⋯V(r)=c_0 \: 𝒥_0 (r) + c_1 \:𝒥_1 (r) + c_2 \:𝒥_2 (r) + c_3 \:𝒥_3 (r) + ⋯ .
        b) Déterminer numériquement les fonctions 𝒥n(r)𝒥_n (r) puis ajuster les coefficients cnc_n donnant  V=CsteV=Cste .
        c) En déduire une représentation graphique de σ(r)σ(r) ; commenter.

4.     • Comparer aux propriétés générales du champ dans la zone entre deux plaques analogues parallèles portant des charges opposées. Commenter.