E.M.VIII - INDUCTION MAGNÉTIQUE

Force électromotrice induite ; loi de Lenz

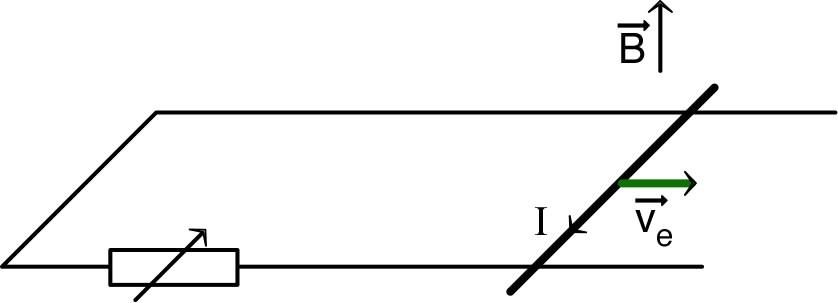
• Dans un champ

\overset{→}{B}

extérieur, la somme des forces de Lorentz appliquées aux charges mobiles donne, sur chaque élément de circuit

\overset{→}{d𝓁}

en mouvement à la vitesse

\overset{→}{v}_e

une force électromotrice induite :

de=\left(\overset{→}{v}_e × \overset{→}{B} \:\right)⋅\overset{→}{d𝓁}

Si le circuit est fermé, la f.e.m. induite est au total :

\displaystyle e=-\frac{dφ_c}{dt}=-\frac{dφ}{dt}

Cette f.e.m. provoque alors un courant dans le sens qui tend à s'opposer à sa cause (loi de Lenz) :

le courant crée un champ induit $\overset{→}{B}_i$ de sens opposé à $\overset{→}{B}$ extérieur ;
la force de Laplace induite due au courant est de sens opposé à $\overset{→}{v}_e$ .

Application à la dynamo

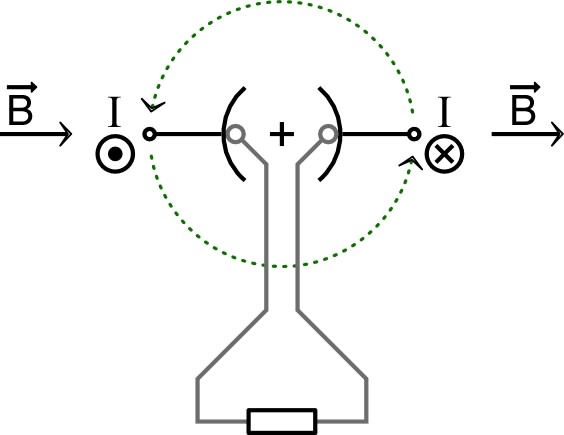
• Un dispositif analogue à celui du moteur à courant continu, utilisé inversement, permet de générer un courant continu à partir d'une action mécanique.

La variation du flux

φ=-B \:h \:R \:θ

impose une f.e.m. constante :

E=B \:S \:ω

Influence du mouvement relatif

• Le déplacement d'un circuit devant un aimant provoque dans le circuit une f.e.m. induite :

\displaystyle e=-\frac{dφ}{dt}

D'un certain point de vue, il peut par contre paraître plus surprenant d'observer le même résultat si on déplace l'aimant devant le circuit fixe : les charges immobiles du circuit ne sont pas soumises à une force de Lorentz.

• D'un autre point de vue, les deux mouvements ne diffèrent que par un changement de référentiel galiléen ; il est donc logique d'observer le même effet.

Cela doit par contre faire réfléchir sur l'invariance de la force de Lorentz dans un tel changement de référentiel ; ici dans l'approximation non relativiste :

$\overset{→}{F}=q \:\overset{→}{v}_e × \overset{→}{B}=q \:\overset{→}{E}'$ .

Ainsi le champ

\overset{→}{B}

de l'aimant, dans son référentiel

ℛ

en mouvement, cause dans le référentiel

ℛ'

du cadre un champ électrique

\overset{→}{E}'

responsable d'une f.e.m. induite équivalente.

◊ remarque : ceci commence à suggérer qu'il est impossible de considérer séparément électricité et magnétisme : il faut une théorie électromagnétique.

📖 exercice n° I.

Application à l'alternateur

• Un façon simple de construire un alternateur rudimentaire consiste à faire tourner une bobine plate selon un axe perpendiculaire à un champ magnétique uniforme et constant :

\displaystyle e=-\frac{dφ}{dt}=-B \:S \: \frac{d}{dt} \left[\cos(ω \,t) \right]=B \:S \; \sin(ω \,t)

◊ remarque : contrairement au cas de la dynamo, les contacts de la bobine doivent ne pas changer à chaque demi-tour.

• En pratique, le rotor est généralement constitué d'un aimant multipolaire (par exemple six paires de pôles

N

S

alternés), en rotation à l'intérieur d'un assemblage coaxial d'un nombre égal de bobines plates de sens alternés.

Loi de Faraday

• Une f.e.m. induite est aussi obtenue avec un électroaimant fixe, provoquant une variation de flux magnétique dans un circuit fixe placé au voisinage.

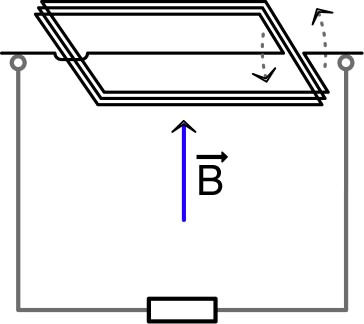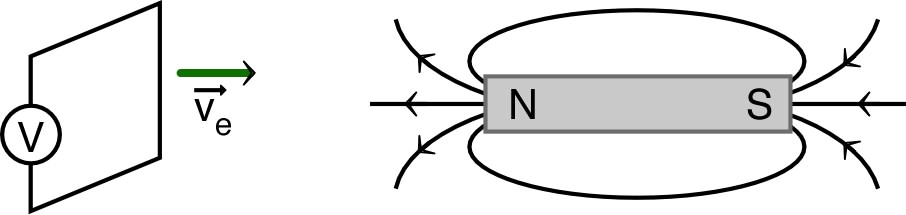
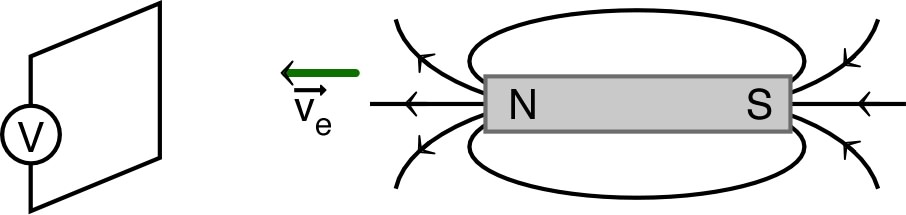
Par cette expérience, Faraday mit en évidence que, de façon générale, il apparaît une f.e.m. induite due à la variation du flux magnétique :

\displaystyle e=-\frac{dφ}{dt}

◊ remarque : l'interprétation, ici plus difficile, conduit à montrer que les équations décrivant les champs électrique et magnétique (équations de Maxwell) ne sont pas indépendantes : toute variation du champ

\overset{→}{B}

crée un champ électrique fonction de

\displaystyle \frac{∂\overset{→}{B}}{∂t}

; ceci est à la base du principe du transformateur.

Inductance propre et inductance mutuelle

• Dans une bobine sans noyau, le flux magnétique de son propre champ est (de même que le champ) proportionnel au courant ; le coefficient est nommé “inductance” :

Φ=L \:I

◊ remarque : si le courant varie, la loi de Faraday impose alors dans la bobine une f.e.m. induite :

\displaystyle e=-L \: \frac{di(t)}{dt}

.

• En particulier, pour un solénoïde de longueur

𝓁

très supérieure au rayon

R

, on peut faire l'approximation d'un champ uniforme :

B≈μ_0 \: n \:I

, avec

\displaystyle n=\frac{N}{𝓁}

.

Le flux à travers l'ensemble des spires est ainsi

Φ≈N \:B \:S

, correspondant à une inductance :

\displaystyle L≈μ_0 \: N^2 \: \frac{S}{𝓁}

.

◊ remarque : pour obtenir des inductances plus grandes avec des bobines petites, on ajoute généralement un noyau en “fer feuilleté” ; cela multiplie le champ magnétique par

≈10

, mais la relation de proportionnalité (

Φ = L \:I

) est moins bien vérifiée (donc la notion d'inductance devient approximative).

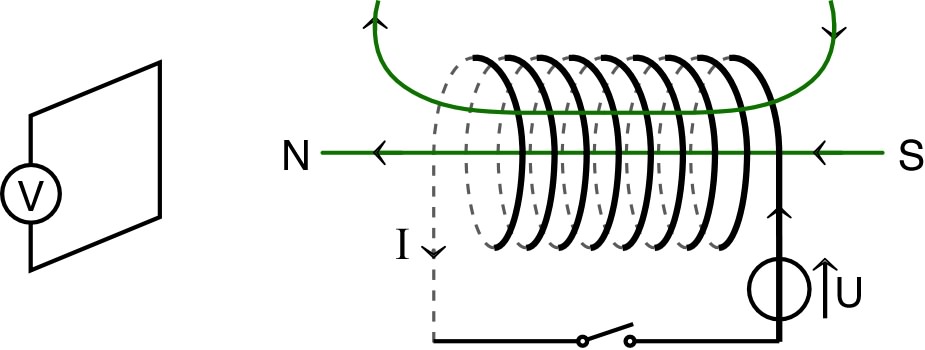
• Quand une bobine est soumise au champ magnétique “extérieur” créé par une autre bobine, la f.e.m. induite découle du flux total :

φ_{tot}=L_1 \: i_1+φ_{2→1}

.

Le flux magnétique causé par la seconde bobine dans la première est de même proportionnel au courant dans la seconde :

φ_{2→1}=M \:i_2

. Le coefficient est nommé “inductance mutuelle” (par opposition,

L

est l'inductance propre).

Le coefficient d'inductance mutuelle décrit l'interaction des deux bobines ; c'est le même pour les deux :

φ_{2→1}=M \:i_2

;

φ_{1→2}=M \:i_1

• On peut ainsi décrire le fonctionnement d'un montage comportant deux bobines en interaction, soumis à un générateur en régime sinusoïdal.

On obtient ainsi :

$\displaystyle L_1 \, \frac{di_1}{dt}+M \, \frac{di_2}{dt}+R_1 \: i_1=u(t)$ ; $\displaystyle M \, \frac{di_1}{dt}+L_2 \, \frac{di_2}{dt}+R_2 \: i_2=0$ .

En régime sinusoïdal permanent, avec les notations complexes :

$(R_1+\mathrm{j} L_1 \, ω) \: \underline{i}_1+\mathrm{j} M \,ω \:\underline{i}_2=\underline{u}$ ; $(R_2+\mathrm{j} L_2 \, ω) \: \underline{i}_2+\mathrm{j} M \,ω \:\underline{i}_1=0$ ;
$\displaystyle \underline{i}_2=-\frac{\mathrm{j} M \,ω}{R_2+\mathrm{j} L_2 \, ω} \: \underline{i}_1$ ; $\underline{u}=\underline{Z} \: \underline{i}_1$ avec $\displaystyle \underline{Z}=R_1+\mathrm{j} L_1 \, ω+\frac{M^2 \, ω^2}{R_2+\mathrm{j} L_2 \, ω}$ .

• Du point de vue énergétique :

$\displaystyle u \:i_1=L_1 \: i_1 \, \frac{di_1}{dt}+M \:i_1 \, \frac{di_2}{dt}+R_1 \: i_1^{\:2}$ ;
$\displaystyle 0=M \,\frac{di_1}{dt} \: i_2+L_2 \: i_2 \, \frac{di_2}{dt}+R_2 \: i_2^{\:2}$ ;
$\displaystyle P=u \:i_1=R_1 \: i_1^{\:2}+R_2 \: i_2^{\:2}+\frac{d}{dt} \left(\frac{1}{2} \, L_1 \: i_1^{\:2}+\frac{1}{2} \, L_2 \: i_2^{\:2}+M \:i_1 \: i_2 \right)$ .

Ceci correspond donc a une généralisation de l'énergie magnétique déjà établie pour une bobine.

📖 exercice n° II.

Courants de Foucault

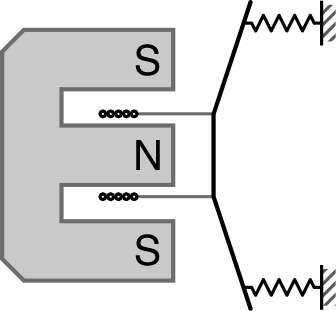
• Dans un matériau conducteur en mouvement relatif par rapport à un aimant, les f.e.m. induites provoquent des “courant de Foucault”.

Conformément à la loi de Lenz, ces courants créent un champ induit qui tend à s'opposer aux variations du champ que subit le matériau.

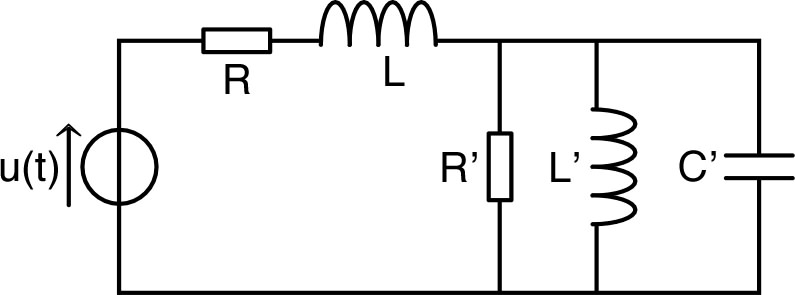• En outre, ces courants causent des forces de Laplace qui tendent à s'opposer au mouvement.

Ainsi, pour éviter que l'élévation de température due au freinage par frottement provoque l'ébullition du liquide de transmission, les camions peuvent être munis de ralentisseurs électromagnétiques (avec un électroaimant au lieu d'un aimant permanent).

• Les plaques de cuisson à induction utilisent un électroaimant en régime alternatif ; elles nécessitent des récipients en matériau ferromagnétique afin que le champ magnétique et les courants induits y soit suffisamment grands (l'énergie ainsi dissipée provoque l'échauffement).

Haut-parleur électrodynamique

• La membrane d'un haut-parleur est fixée sur le support par une partie élastique se comportant comme un ressort. Son centre est solidaire d'une bobine qui peut se déplacer selon l'axe d'un aimant torique.

Sous l'effet d'un générateur (non représenté) la bobine est parcourue par un courant

i

(on oriente ce courant d'après le sens de l'axe horizontal). Elle subit de ce fait une force de Laplace

F=-i \:𝓁 \:B

.

Lors de l'émission sonore, l'interaction entre la membrane et l'air peut être décrite par une force de frottement fluide

f=-α \:\dot{x}

.

L'équation mécanique est donc de la forme :

m \:\ddot{x}+α \:\dot{x}+k \:x=-i \:𝓁 \:B

.

• Le circuit électrique subit au total une f.e.m. induite :

\displaystyle e=- L \:\overset{\:ₒ}{i}+B \:𝓁 \:\dot{x}

.

L'équation électrique est de la forme :

\displaystyle u-R \:i-L \:\overset{\:ₒ}{i}=-B \:𝓁 \:\dot{x}

.

◊ remarque : si on la juge ambigüe, on peut préférer éviter la notation

\displaystyle \overset{\:ₒ}{i}≝\frac{di}{dt}

.

◊ remarque : en régime sinusoïdal, le haut-parleur se comporte ainsi au total comme une impédance équivalente :

\displaystyle \underline{Z}=R+\mathrm{j} L \,ω+\frac{B^2 \: 𝓁^2}{\mathrm{j} m \:ω+\frac{k}{\mathrm{j} ω}+α}

; le dernier terme peut être schématisé par l'association en parallèle d'une résistance

\displaystyle R'=\frac{B^2 \: 𝓁^2}{α}

, d'une inductance

\displaystyle L'=\frac{B^2 \: 𝓁^2}{k}

et d'une capacité

\displaystyle C'=\frac{m}{B^2 \: 𝓁^2}

.

• Du point de vue énergétique :

$u \:i=R \:i^2+L \:i \:\overset{\:ₒ}{i}-i \:B \:𝓁 \:\dot{x}$ ;
$m \:v \:\dot{v}+α \:v^2+k \:x \:\dot{x}=-i \:𝓁 \:B \:\dot{x}$ ;
$\displaystyle P=u \:i=R \:i^2+\frac{d}{dt} \left(\frac{1}{2} L \:i^2 \right)+α \:v^2+\frac{d}{dt} \left(\frac{1}{2} m \:v^2+\frac{1}{2} k \:x^2 \right)$ .

📖 exercice n° III.