INDUCTION MAGNÉTIQUE - corrigé du TP


Observations qualitatives

Rails de Laplace et flux coupé

• Lors du déplacement du barreau sur les rails, il faut prendre soin à bien le maintenir appuyé, pour éviter les faux contacts dus à l'oxydation en surface du métal.

Sinon, on peut observer un phénomène autre que celui escompté : lors d'un mauvais contact, le circuit se comporte comme s'il comportait une grande résistance en série ; or, une grande résistance se comporte comme une antenne radio et capte de nombreux parasites (surtout à 50Hz50 \:\mathrm{Hz} à cause du réseau de distribution de l'énergie électrique). De tels parasites peuvent souvent être plus de dix fois supérieurs au phénomène étudié ici.

Mouvement relatif


Expérience de Faraday


Courants de Foucault


Alternateur

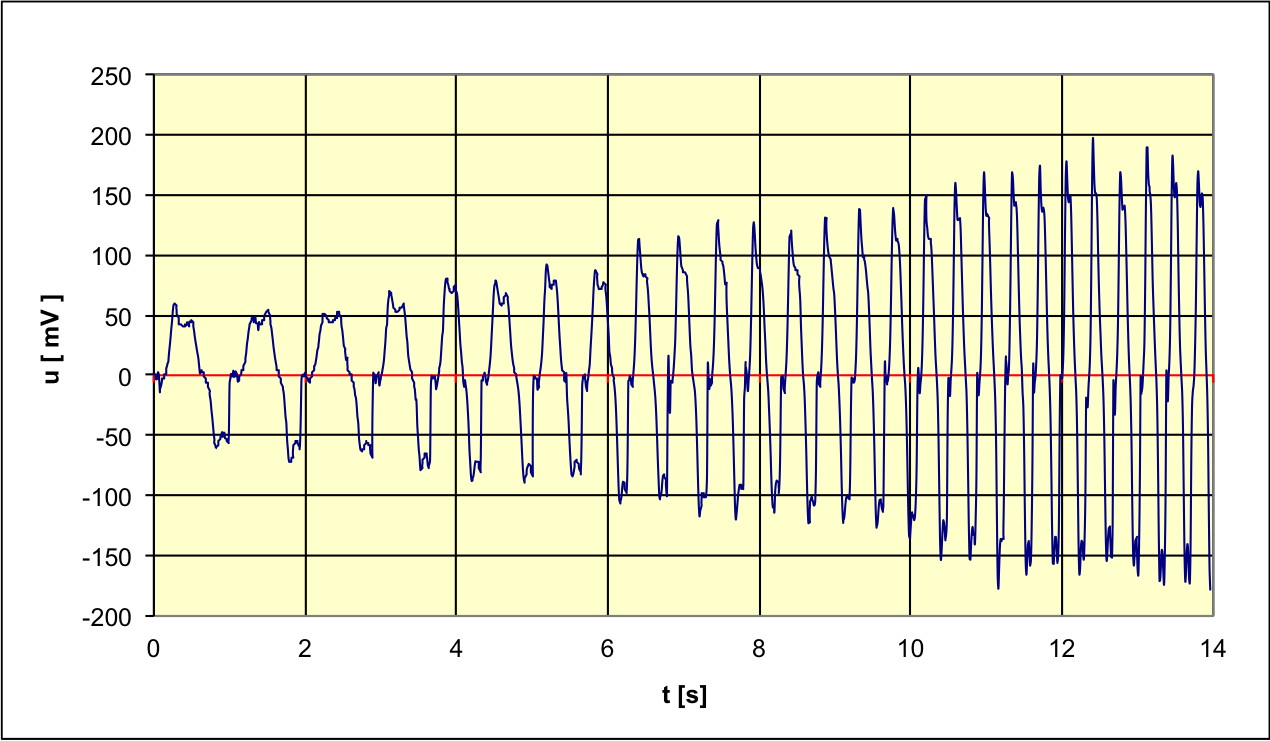
• On peut ici ne pas se limiter à une étude qualitative : on peut commencer avec une rotation lente, puis augmenter progressivement la vitesse afin d'obtenir un enregistrement comportant toute une gamme de fréquences.

induction_corTP_Im/alternateur_1.jpg

• Il n'est pas facile de mesurer précisément l'amplitude d'un signal dont la forme n'est pas régulière (à cause de la vitesse de rotation, qu'il est difficile de contrôler précisément). C'est encore moins évident de comparer ensuite les valeurs ainsi obtenues.

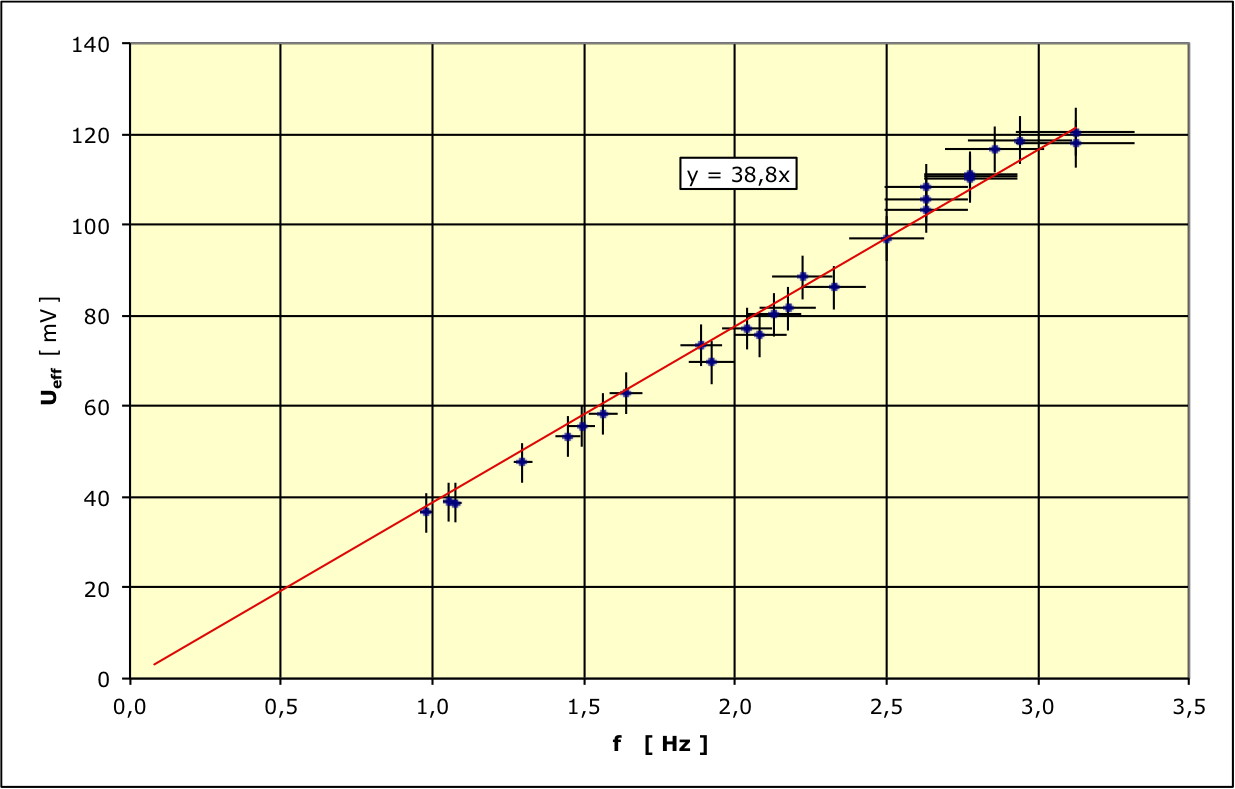
On peut alors utiliser les “moyennes” que sont les valeurs efficaces  Ueff=1T∫u2(t)dt U_\text{eff}=\sqrt{\,{\displaystyle{\frac{1}{T}}} \, ∫ u^2 (t) \: dt}   avec  T=∫dtT=∫ dt .  En transférant les mesures dans un tableur on calcule  Ueff≈1T∑[u2(tk)Δt]U_\text{eff}≈\sqrt{\, {\displaystyle{\frac{1}{T} \: ∑}} \left[u^2 (t_k ) \; Δt\right]}   où  Δt=tk+1−tkΔt=t_{k+1}-t_k .

Il est possible de vérifier que le produit de l'amplitude par la période est constante, ou que l'amplitude est proportionnelle à la fréquence. Ceci s'interprète par le fait que la f.e.m. peut s'écrire :  e=−dφdt=−dφdθdθdt\displaystyle e=-\frac{dφ}{dt}=-\frac{dφ}{dθ} \, \frac{dθ}{dt}  où  dθdt=2πf\displaystyle \frac{dθ}{dt}=2π \:f  et où le terme dφdθ\displaystyle \frac{dφ}{dθ} reste constant puisqu'il ne dépend que de la géométrie du montage.

induction_corTP_Im/alternateur_2.jpg

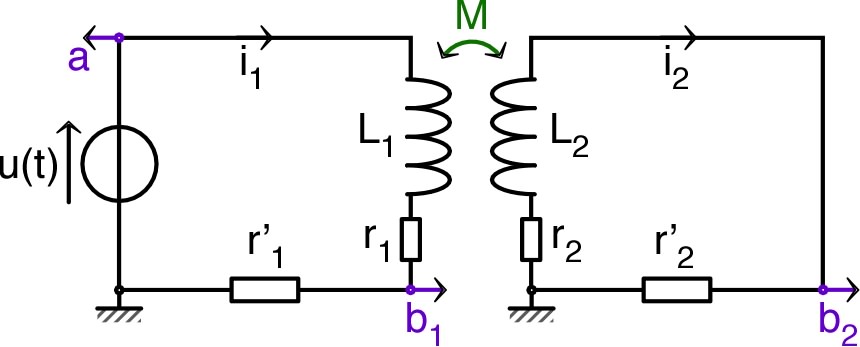
Bobines en interaction

• On utilise deux bobines de 10001000 spires accolées (coefficient d'interaction maximum en l'absence de noyau). On mesure :  L1=44,7±0,5mHL_1=44\text{,}7±0\text{,}5 \:\mathrm{mH}  ;  r1=8,59±0,08Ωr_1=8\text{,}59±0\text{,}08 \:\mathrm{Ω}  ;  L2=44,9±0,5mHL_2=44\text{,}9±0\text{,}5 \:\mathrm{mH}  ;  r2=8,51±0,08Ωr_2=8\text{,}51 ± 0\text{,}08 \:\mathrm{Ω} .

On ajoute en série :  r1′=10,00±0,005Ωr'_1=10\text{,}00±0\text{,}005 \:\mathrm{Ω}  (c'est-à-dire  R1=18,59±0,09ΩR_1=18\text{,}59±0\text{,}09 \:\mathrm{Ω} )  ;  r2′=10,00±0,005Ωr'_2=10\text{,}00±0\text{,}005 \:\mathrm{Ω}  (donc  R2=18,51±0,09ΩR_2=18\text{,}51 ± 0\text{,}09 \:\mathrm{Ω} ).

induction_corTP_Im/induction_corTP_Im1.jpg

• On obtient ainsi en régime sinusoïdal, avec les notations complexes :
(R1+jωL1)I_1+jωMI_2=U_(R_1+\mathrm{j} \,ω \:L_1 ) \: \underline{I}_1+\mathrm{j} \,ω \:M \:\underline{I}_2=\underline{U}   ;   (R2+jωL2)I_2+jωMI_1=0(R_2+\mathrm{j} \,ω \:L_2 ) \: \underline{I}_2+\mathrm{j} \,ω \:M \: \underline{I}_1=0 .

On en déduit :  I_2=H_I_1\underline{I}_2=\underline{H} \: \underline{I}_1  avec  H_=−jωMR2+jωL2\displaystyle \underline{H}=-\frac{\mathrm{j} \,ω \:M}{R_2+\mathrm{j} \,ω \:L_2}  ;  U_=Z_I_1\underline{U}=\underline{Z} \: \underline{I}_1  avec  Z_=R1+jωL1+ω2M2R2+jωL2\displaystyle \underline{Z}=R_1+\mathrm{j} \,ω \:L_1+\frac{ω^2 \: M^2}{R_2+\mathrm{j} \,ω \:L_2} .

• À la fréquence  f=72,10±0,14Hzf=72\text{,}10±0\text{,}14 \:\mathrm{Hz}  on mesure :
U1=845±4mVU_1=845±4 \:\mathrm{mV}  ;  U2=87,8±0,4mVU_2=87\text{,}8±0\text{,}4 \:\mathrm{mV}  ;  φ2/1=−140°±3°φ_{2/1}=-140 \,°±3 \,° .

On peut tester la cohérence en calculant  φ2/1=−π2−arctan(ωL2R2)=−137,7°±0,4°\displaystyle φ_{2/1}=-\frac{π}{2}-\arctan\left(\frac{ω \:L_2}{R_2} \right)=-137\text{,}7 \,°±0\text{,}4 \,° .

Ceci correspond à  H=r1′r2′U2U1=0,1039±0,0008\displaystyle H=\frac{r'_1}{r'_2} \, \frac{U_2}{U_1} =0\text{,}1039±0\text{,}0008 .  On en déduit  M=HωR22+ω2L22=6,31±0,09mH\displaystyle M=\frac{H}{ω} \: \sqrt{R_2^{\:2}+ω^2 \: L_2^{\:2}}=6\text{,}31±0\text{,}09 \:\mathrm{mH} .

◊ remarque : on obtient  M≪L1≈L2M≪L_1≈L_2  car, en l'absence de noyau, les lignes de champ de chaque bobine divergent rapidement dès qu'on s'en éloigne.

• On mesure ensuite :  U=2,340±0,012VU=2\text{,}340±0\text{,}012 \:\mathrm{V}  ;  φ1=48°±2°φ_1=48 \,°±2 \,°  (en faisant attention à la convention de signe inversée pour mesurer i1i_1 ). Ceci donne  Z=r1′UU1=27,7±0,2Ω\displaystyle Z=r'_1 \, \frac{U}{U_1} =27\text{,}7±0\text{,}2 \:\mathrm{Ω} .
Par ailleurs  Z_=R1+jωL1+H2.(R2−jωL2)\underline{Z}=R_1+\mathrm{j} \,ω \:L_1+H^2.(R_2-\mathrm{j} \,ω \:L_2 )  avec  H2=ω2M2R22+ω2L22\displaystyle H^2=\frac{ω^2 \: M^2}{R_2^{\:2}+ω^2 \: L_2^{\:2}}  ;  on est donc en principe ramené à résoudre l'équation donnant H H puis MM :  Z2=(R1+H2R2)2+(ωL1−H2ωL2)2Z^2=(R_1+H^2 \: R_2 )^2+(ω \:L_1-H^2 \: ω \:L_2 )^2 .

• Cette équation est toutefois moins utile car la faible valeur de MM fait que l'influence sur ZZ est très petite ; ainsi en déduire inversement MM est moins précis.

On se limite donc à vérifier que le résultat :  Z=27,5±0,1ΩZ=27\text{,}5±0\text{,}1 \:\mathrm{Ω}  est compatible avec la solution obtenue précédemment.

Le déphasage est  φ1=arctan(ωL1−H2ωL2R1+H2R2)=46,8°±0,6°\displaystyle φ_1=\arctan\left(\frac{ω \:L_1-H^2 \: ω \:L_2}{R_1+H^2 \: R_2}\right)=46\text{,}8 \,°±0\text{,}6 \,°  ;  de même compatible.


• À la fréquence  f=189,6±0,4Hzf=189\text{,}6±0\text{,}4 \:\mathrm{Hz}  on mesure :
U1=712±4mVU_1=712±4 \:\mathrm{mV}  ;  U2=96,6±0,5mVU_2=96\text{,}6±0\text{,}5 \:\mathrm{mV}  ;  φ2/1=−162°±3°φ_{2/1}=-162 \,°±3 \,° .

On peut tester la cohérence en calculant  φ2/1=−π2−arctan(ωL2R2)=−160,9°±0,4°\displaystyle φ_{2/1}=-\frac{π}{2}-\arctan\left(\frac{ω \:L_2}{R_2} \right)=-160\text{,}9 \,°±0\text{,}4 \,° .

Ceci correspond à  H=r1′r2′U2U1=0,1357±0,0009\displaystyle H=\frac{r'_1}{r'_2} \: \frac{U_2}{U_1} =0\text{,}1357±0\text{,}0009 .  On en déduit  M=HωR22+ω2L22=6,45±0,09mH\displaystyle M=\frac{H}{ω} \: \sqrt{R_2^{\:2}+ω^2 \: L_2^{\:2}}=6\text{,}45±0\text{,}09 \:\mathrm{mH} .
Ce résultat semble confirmer celui obtenu à la première fréquence.

• On mesure ensuite :  U=4,025±0,020VU=4\text{,}025±0\text{,}020 \:\mathrm{V}  ;  φ1=72°±2°φ_1=72 \,°±2 \,° . Ceci donne  Z=r1′UU1=56,5±0,5Ω\displaystyle Z=r'_1 \, \frac{U}{U_1} =56\text{,}5±0\text{,}5 \:\mathrm{Ω} .

La valeur obtenue pour MM donne ici :  Z=55,6±0,2ΩZ=55\text{,}6±0\text{,}2 \:\mathrm{Ω}  et  φ1=70,1°±0,7°φ_1=70\text{,}1 \,°±0\text{,}7 \,°  ;  ces valeurs sont ici encore compatibles.


• À la fréquence  f=561,0±1,1Hzf=561\text{,}0±1\text{,}1 \:\mathrm{Hz}  on mesure :
U1=369,2±1,8mVU_1=369\text{,}2±1\text{,}8 \:\mathrm{mV}  ;  U2=52,3±0,3mVU_2=52\text{,}3±0\text{,}3 \:\mathrm{mV}  ;  φ2/1=−172°±3°φ_{2/1}=-172 \,°±3 \,° .

On peut tester la cohérence en calculant  φ2/1=−π2−arctan(ωL2R2)=−173,3°±0,4°\displaystyle φ_{2/1}=-\frac{π}{2}-\arctan\left(\frac{ω \:L_2}{R_2} \right)=-173\text{,}3 \,°±0\text{,}4 \,° .

Ceci correspond à  H=r1′r2′U2U1=0,1417±0,0010\displaystyle H=\frac{r'_1}{r'_2} \, \frac{U_2}{U_1} =0\text{,}1417±0\text{,}0010 .  On en déduit  M=HωR22+ω2L22=6,40±0,09mH\displaystyle M=\frac{H}{ω} \: \sqrt{R_2^{\:2}+ω^2 \: L_2^{\:2}}=6\text{,}40±0\text{,}09 \:\mathrm{mH} .
Ce résultat semble confirmer ceux obtenus aux deux premières fréquences.

• On mesure ensuite :  U=5,812±0,029VU=5\text{,}812±0\text{,}029 \:\mathrm{V}  ;  φ1=82°±2°φ_1=82 \,°±2 \,° .  Ceci donne  Z=r1′UU1=157,4±1,4Ω\displaystyle Z=r'_1 \, \frac{U}{U_1} =157\text{,}4±1\text{,}4 \:\mathrm{Ω} .

La valeur obtenue pour MM donne ici :  Z=155,5±0,6ΩZ=155\text{,}5±0\text{,}6 \:\mathrm{Ω}  et  φ1=83,0°±0,8°φ_1=83\text{,}0 \,°±0\text{,}8 \,°  ;  ces valeurs sont de même compatibles.


• Au total, on obtient finalement en moyenne :  M=6,39±0,08mHM=6\text{,}39±0\text{,}08 \:\mathrm{mH} .

Il peut par contre être plus précis de n'utiliser que ff et UU (en plus des caractéristiques des composants) pour calculer théoriquement les autres mesures (U1U_1 , U2U_2 , φ1φ_1 et φ2/1φ_{2/1} ) en fonction de MM , puis d'ajuster la valeur de MM de façon à minimiser le χ2χ^2 entre théorie et mesures.

Le résultat est plus long à calculer (surtout pour estimer des incertitudes), mais il est plus précis car il utilise alors l'ensemble des informations expérimentales fournies par les mesures :  M=6,31±0,04mHM=6\text{,}31±0\text{,}04 \:\mathrm{mH} .

◊ remarque : en outre, la valeur obtenue  χ2=8,27χ^2=8\text{,}27  pour 1111 degrés de liberté (1212 mesures et un paramètre) donne une probabilité 69%69 \,% ; cette valeur est correcte car les incertitudes utilisées correspondent plutôt à un écart standard ; en utilisant des incertitudes à deux écarts standard, on obtient une probabilité 99,8% 99,8 \,% .