ÉM.V - CHAMP MAGNÉTOSTATIQUE

Densité de courant

• On se limite ici aux champs magnétostatiques créés par des courants permanents (pour des circuits immobiles parcourus par des courants continus).

• De même qu’on décrit la répartition des charges par une “densité volumique de charge” :

\displaystyle ρ=\frac{dQ}{dτ}

, on peut décrire la “répartition” du courant à travers la section d’un conducteur par une “densité de courant” :

\overset{→}{j}=∑ \:ρ_i \: 〈\overset{→}{v}_i 〉

(somme sur types de porteurs de charge) telle que le courant à travers la section d’un conducteur soit :

I=∬ \:\overset{→}{j}⋅d\overset{→}{S}

.

◊ remarque : on ajoute constructivement les contributions des porteurs de charge positifs et négatifs.

• On se limite ici à l’étude de circuits “filiformes” (on ignore la répartition du courant, donc l'étude est moins approfondie que celle de l’électrostatique).

Loi de Biot et Savart pour un circuit filiforme

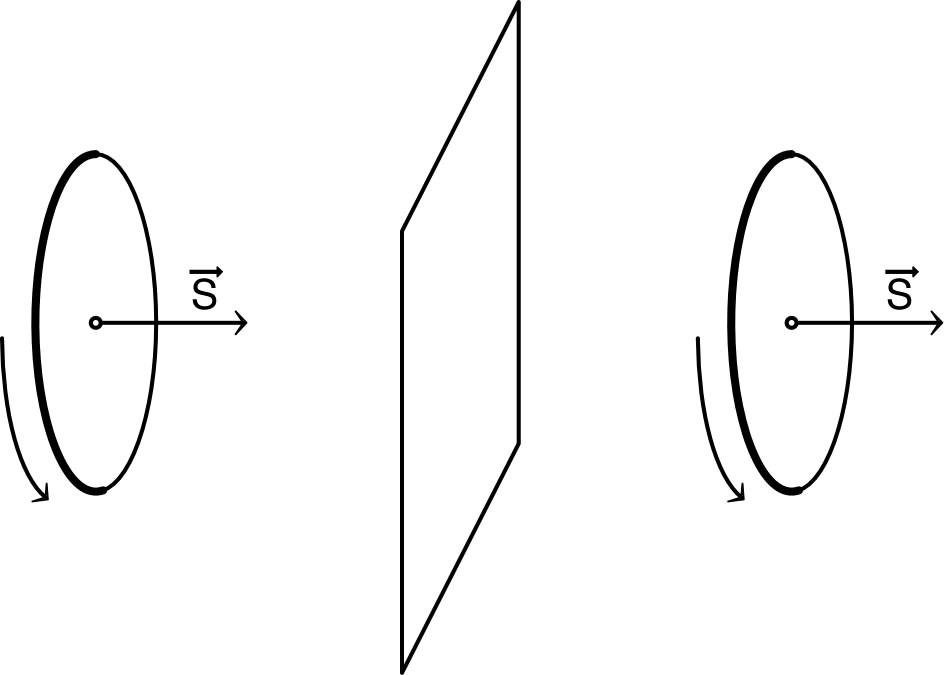
• Pour un circuit (fermé) filiforme orienté

C

, parcouru par un courant

I

constant (on oriente le circuit dans le sens du courant), le champ magnétique créé en un point

M

peut s’écrire (loi de Biot et Savart) :

\displaystyle \overset{→}{B}=\frac{μ_0}{4π} \, ∫_C \frac{I \:d\overset{→}{𝓁} × \overset{→}{u}_r}{r^2}

avec

d\overset{→}{𝓁}=d\overset{⟶}{OP}

“élément infinitésimal du circuit” ;

r=PM

;

\displaystyle \overset{→}{u}_r=\frac{\overset{⟶}{PM}}{r}

;

$\displaystyle μ_0=\frac{1}{ε_0 \: c^2}≈4π.{10}^{-7} \: \mathrm{H.m^{-1}}$ “perméabilité magnétique du vide”.

• À cause du produit vectoriel, la contribution

\displaystyle \overset{→}{dB}=\frac{μ_0}{4π} \: \frac{I \:\overset{→}{d𝓁} × \overset{→}{u}_r}{r^2}

à l’intégrale est orthoradiale (la contribution analogue en électrostatique est radiale).

De ce fait, le champ magnétique

\overset{→}{B}

est un “pseudo-vecteur” ; c’est-à-dire que, pour une symétrie plane, il est transformé en l’opposé de son “symétrique” géométrique (de même qu’un “vecteur surface”

\overset{→}{S}

Application au calcul du champ magnétique

Fil rectiligne “infini”

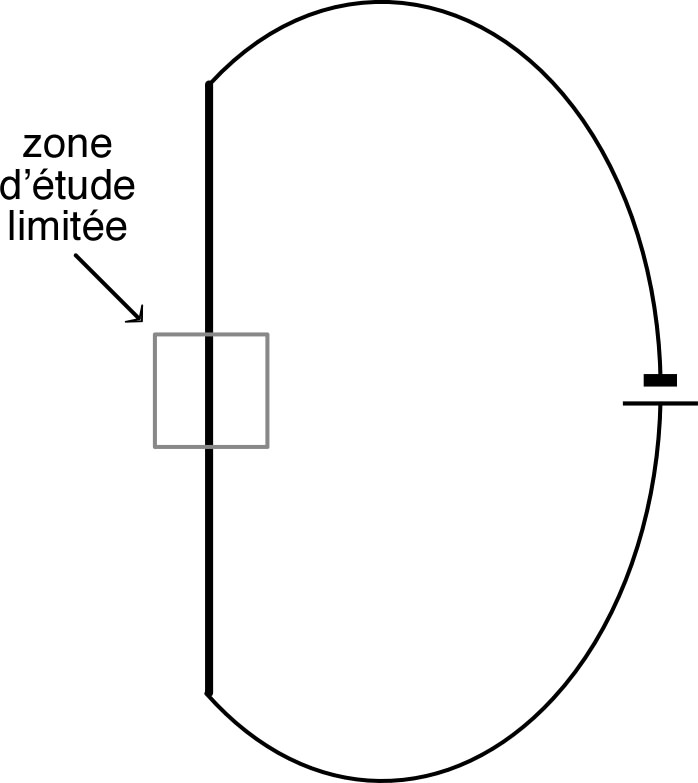
• En plus du problème de “l’infini”, un fil rectiligne infini n’est pas un circuit (fermé) ; a priori, on ne peut donc pas lui appliquer la loi de Biot et Savart.

En réalité, le modèle du fil rectiligne infini représente une portion rectiligne d’un circuit dont on limite l’étude à de faibles distances, de telle sorte que le “reste” (non rectiligne) du circuit ait un effet négligeable.

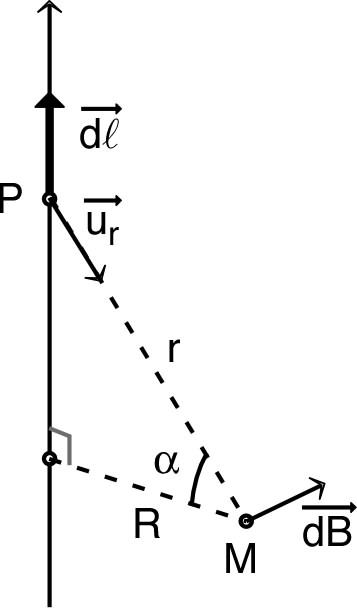
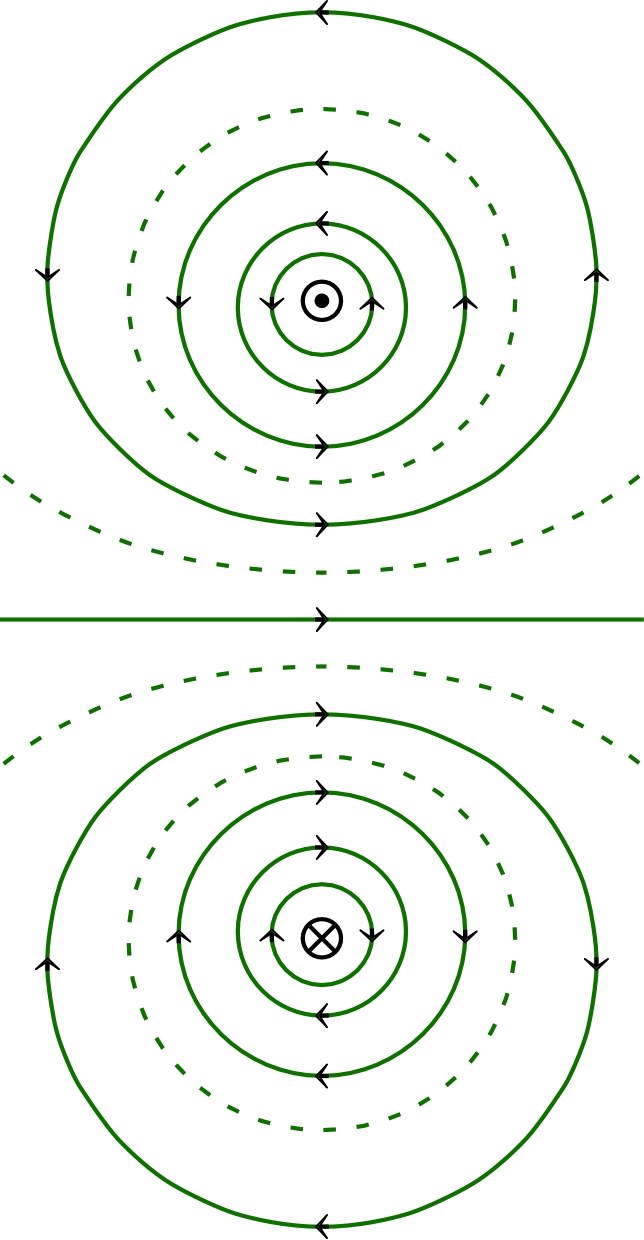
• Pour un tel modèle les invariances, par rotation autour de l’axe et par translation selon l’axe, conduisent à utiliser des coordonnées cylindriques.

L’expression algébrique des coordonnées du champ en un point

M

ne peut alors dépendre que de la distance

R

entre le fil et le point

M

.

En outre, puisque chaque contribution :

$\displaystyle d\overset{→}{B}=\frac{μ_0}{4π} \: \frac{I \:\overset{→}{d𝓁} × \overset{→}{u}_r}{r^2} =\frac{μ_0}{4π} \: \frac{I \:d𝓁}{r^2} \: \cos(α) \: \overset{→}{u}_θ$

est perpendiculaire au plan défini par le fil et

M

, il en est de même pour

\overset{→}{B}

total.

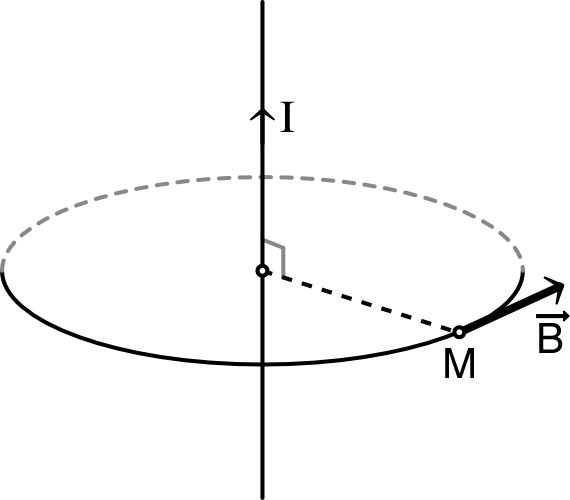
On peut ainsi écrire en coordonnées cylindriques :

\overset{→}{B}=B_θ (R) \: \overset{→}{u}_θ

.

Les lignes de champ sont donc des cercles perpendiculaires au fil et centrés sur lui ; elles sont orientées dans le sens de rotation positif par rapport au sens du courant.

◊ remarque : le fil et

M

sont invariants par symétrie selon le plan qu'ils définissent, donc

\overset{→}{B}

l’est aussi ; ainsi

\overset{→}{B}≘B_R \: \overset{→}{u}_R+B_θ \: \overset{→}{u}_θ+B_z \: \overset{→}{u}_z

(pseudovecteur représenté par un vecteur) est identique à l’opposé du vecteur symétrique :

\overset{→}{B}=𝒮\left(\overset{→}{B} \,\right)≘-𝒮(B_R \: \overset{→}{u}_R+B_θ \: \overset{→}{u}_θ+B_z \: \overset{→}{u}_z )=-B_R \: \overset{→}{u}_R+B_θ \: \overset{→}{u}_θ-B_z \: \overset{→}{u}_z

; ainsi

B_R

B_z

doivent être nulles.

• On peut intégrer :

\displaystyle dB_θ=d\overset{→}{B}⋅\overset{→}{u}_θ=\frac{μ_0 \: I}{4π} \: \frac{d𝓁 \:\cos(α)}{r^2}

avec :

$r=\sqrt{R^2+z^2}$ ; $\displaystyle \cos(α)=\frac{R}{r}$ ; $z=R \; \tan(α)$ ; $d𝓁=dz$ .

On obtient :

\displaystyle B_θ=\frac{μ_0 \: I}{4π}\: ∫_{-∞}^∞ \,\frac{R\quad}{\left(R^2+z^2 \right)^{3/2}} \: dz=\frac{μ_0 \: I}{4π} \: ∫_{-π/2}^{π/2} \frac{\cos(α)}{R} \: dα=\frac{μ_0 \: I}{2π \:R}

Spire circulaire (champ sur l’axe)

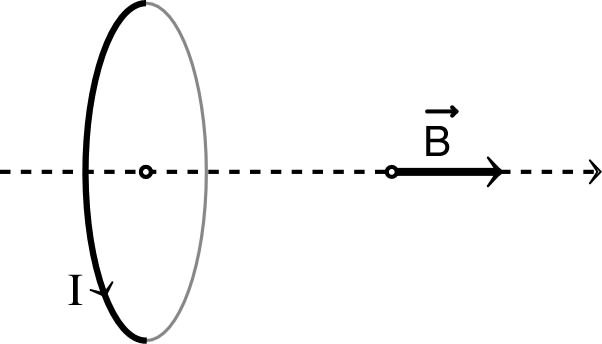
• On cherche le champ

\overset{→}{B}

d’une spire circulaire de rayon

R

et d’axe

Ox

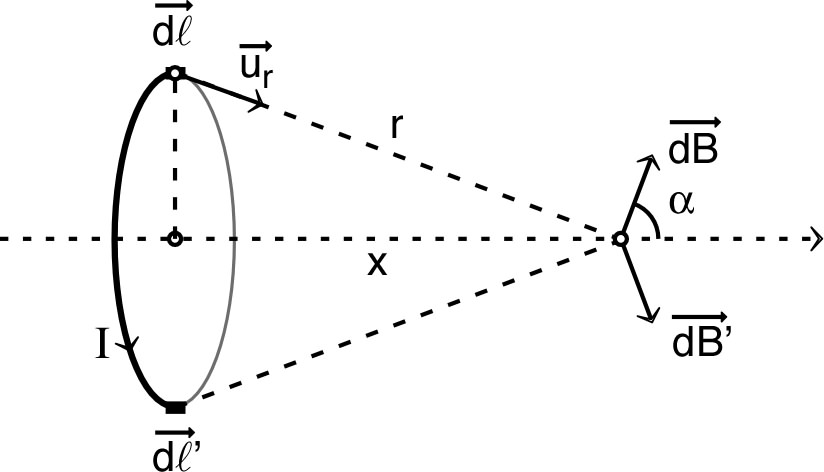
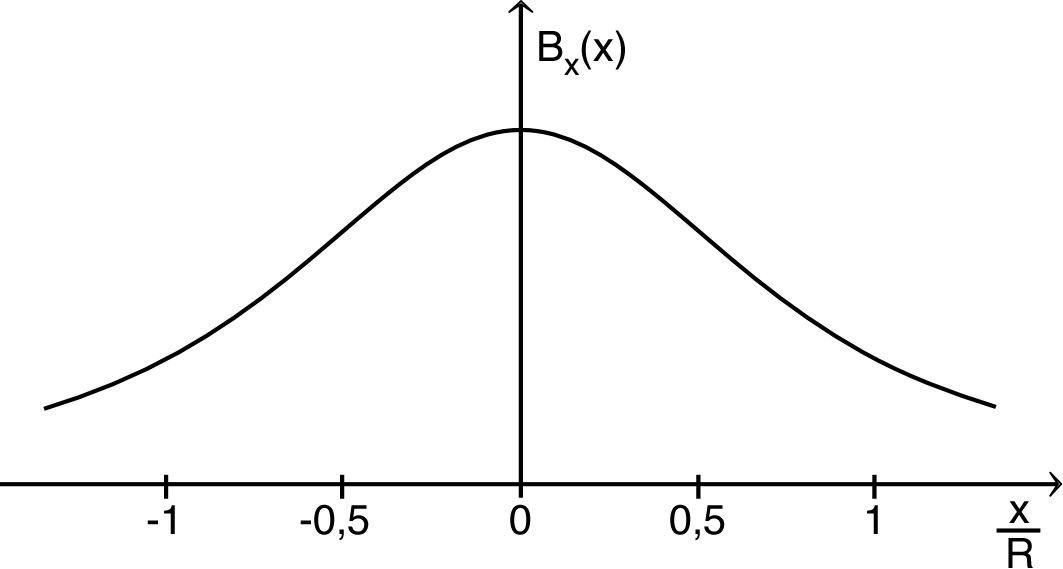
, en se limitant aux points de l’axe.

Sur l’axe, le champ est selon

Ox

(dans le sens axial positif par rapport au sens de rotation du courant) :

\overset{→}{B}=B_x \: \overset{→}{u}_x

En effet, les contributions

$\displaystyle d\overset{→}{B}=\frac{μ_0}{4π} \: \frac{I \:\overset{→}{d𝓁} × \overset{→}{u}_r}{r^2}$

de deux éléments

\overset{→}{d𝓁}

\overset{→}{d𝓁}'

symétriques ont des projections qui se compensent dans les directions perpendiculaires à

Ox

• En intégrant :

\displaystyle dB_x=\frac{μ_0 \: I \:d𝓁}{4π \:r^2} \: \cos(α)

avec

r=\sqrt{R^2+x^2}

;

\displaystyle \cos(α)=\frac{R}{r}

d𝓁=R \:dθ

; on obtient :

\displaystyle B_x=\frac{μ_0 \: I \:R^2}{2 \,\left(R^2+x^2 \right)^{3/2}}

◊ remarque : pour une bobine plate constituée de

N

spires, il suffit de multiplier par

N

; on retrouve en particulier au centre de la spire :

\displaystyle B_x=\frac{μ_0 \: N \:I}{2 \,R}

.

◊ remarque : les champs magnétiques des aimants sont dus à des courants analogues au niveau microscopique.

Bobines de Helmholtz

• Pour un ensemble de deux spires circulaires de rayon

R

et d’axe

Ox

, placées en

x_0

-x_0

et parcourues par le même courant

I

(de même sens) ; on cherche la valeur de

x_0

telle que le champ magnétique au voisinage du centre du dispositif soit le plus uniforme possible (en se limitant aux points de l’axe).

Puisque le champ est selon l’axe :

B_x=B_{1x}+B_{2x}

. Par symétrie, le champ est forcément extremum au centre, avec :

\displaystyle \frac{dB_x}{dx}=0

;

\displaystyle \frac{d^3 B_x}{{dx}^3} =0

. On peut donc écrire :

\displaystyle B_x (x)≈B_x (0)+\frac{d^2 B_x}{{dx}^2} \: \frac{x^2}{2!}+\frac{d^4 B_x}{{dx}^4} \: \frac{x^4}{4!}+⋯

Pour que le champ soit le plus uniforme possible il faut en plus :

\displaystyle \frac{d^2 B_x}{{dx}^2} =0

, ce qui correspond à

\displaystyle x_0=\frac{R}{2}

(distance

R

entre les deux bobines).

Dans ce cas, le champ est d'ailleurs aussi quasi-uniforme radialement. Le dispositif ainsi ajusté (bobines de Helmholtz) est très pratique pour obtenir simplement une zone de champ magnétique quasi-uniforme et facile d'accès.

Solénoïde

• Pour calculer le champ sur l’axe d’un solénoïde de

N

spires et de longueur

L

, on considère une “bobine plate infinitésimale” d’épaisseur

dx_0

et comportant

\displaystyle \frac{N}{L} \: dx_0

spires, puis on intègre pour

x_0

variant de

\displaystyle -\frac{L}{2}

\displaystyle \frac{L}{2}

.

On obtient ainsi :

\displaystyle B_x (x)=\frac{μ_0 \: N \:I}{2 \,L} \; \left[\frac{x+\frac{L}{2}}{\sqrt{R^2+\left(x+\frac{L}{2}\right)^2}}-\frac{x-\frac{L}{2}}{\sqrt{R^2+\left(x-\frac{L}{2}\right)^2}}\right]

.

En pratique, le solénoïde crée :

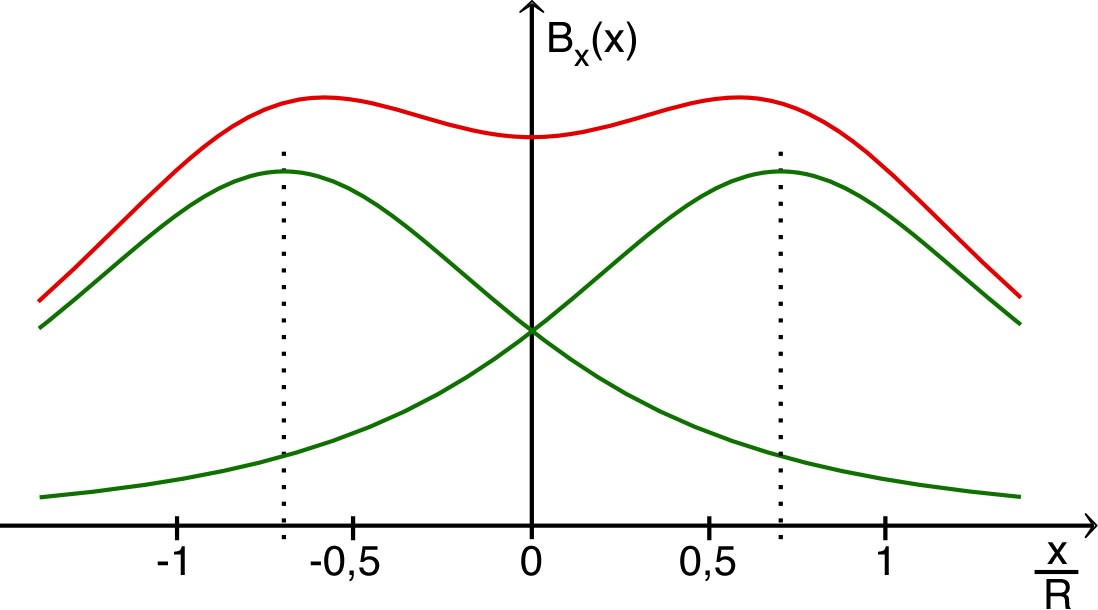
◊	à l'extérieur un champ semblable à celui d'un barreau aimanté ;
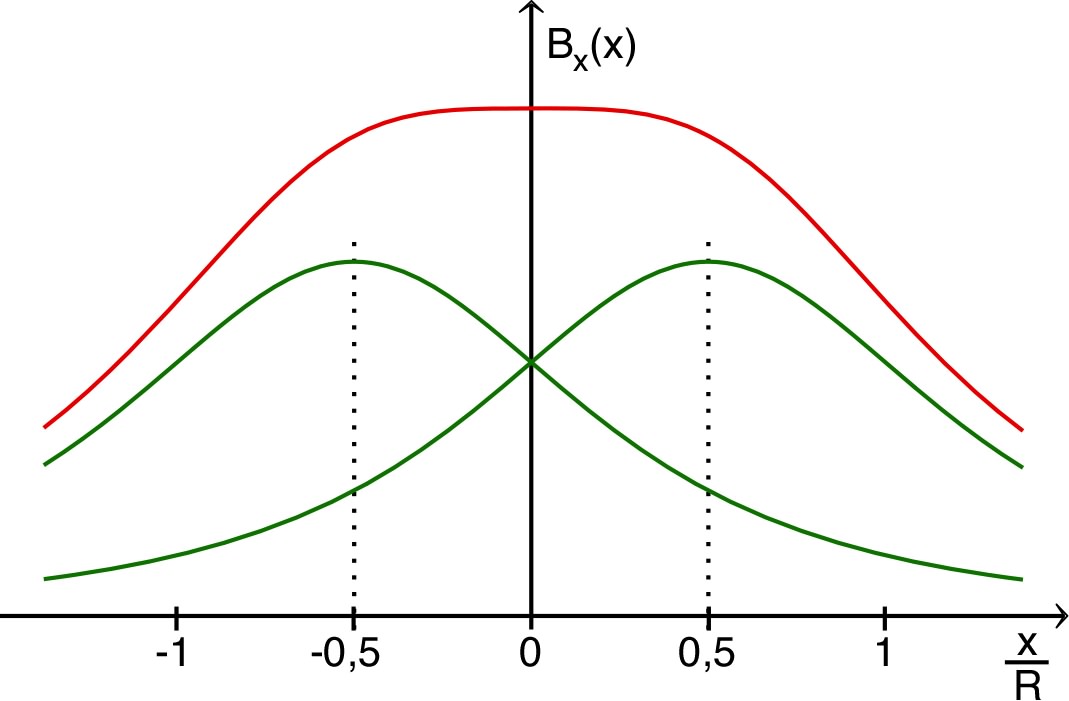
◊	à l'intérieur un champ quasi-uniforme, de norme $B≈μ_0 \: n \:I$ (indépendante du rayon) avec $\displaystyle n=\frac{N}{L}$ .

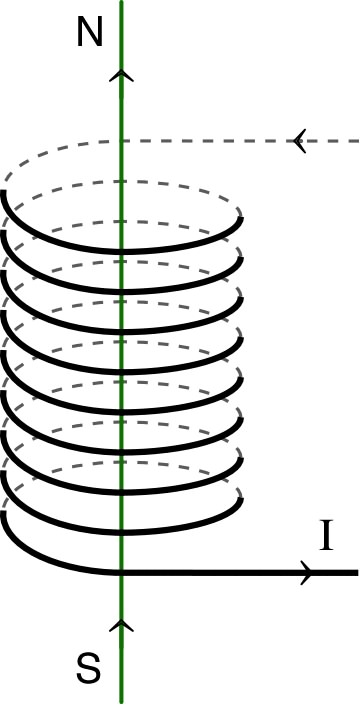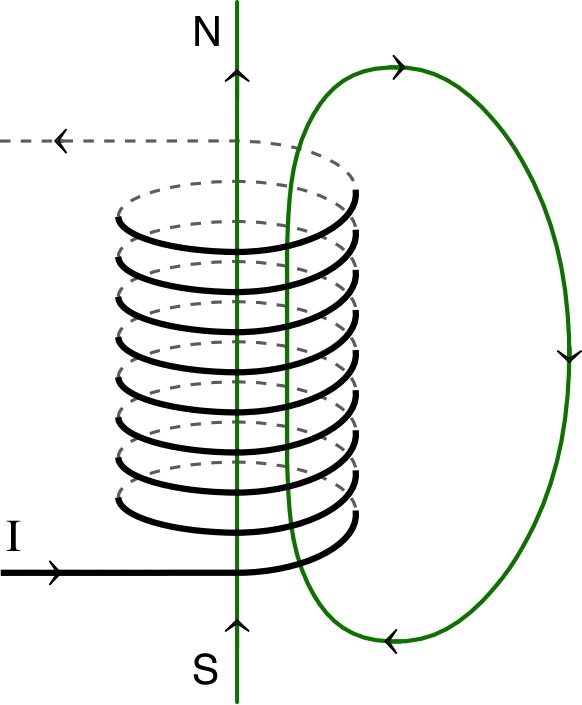
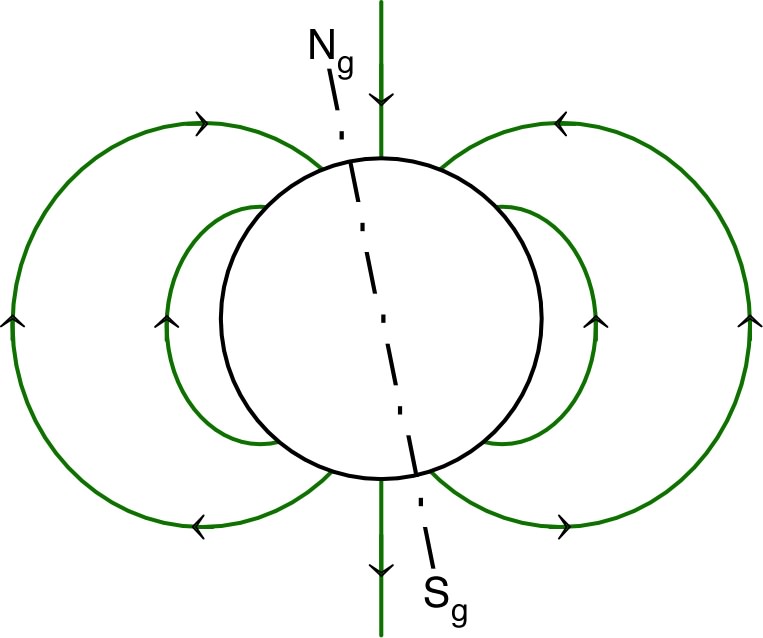
◊ remarque : une bobine parcourue par un courant se comporte comme un aimant dont les pôles nord et sud sont liés au sens de rotation du courant dans les spires ; en particulier l'orientation du champ ne dépend pas du côté par où arrive le courant, mais uniquement du sens de rotation.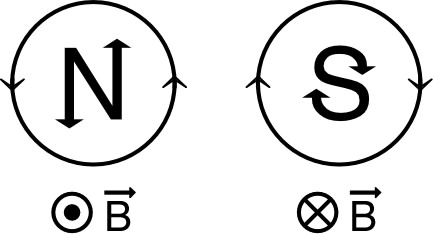

◊ remarque : la terre a un pôle magnétique sud au voisinage du pôle géographique nord et réciproquement (mais l’étude de la croûte terrestre montre que les pôles s’inversent tous les quelques millions d’années).

◊ remarque : le champ magnétique terrestre comporte une composante verticale

📖 exercices n° I, II et III.

Dipôle magnétique

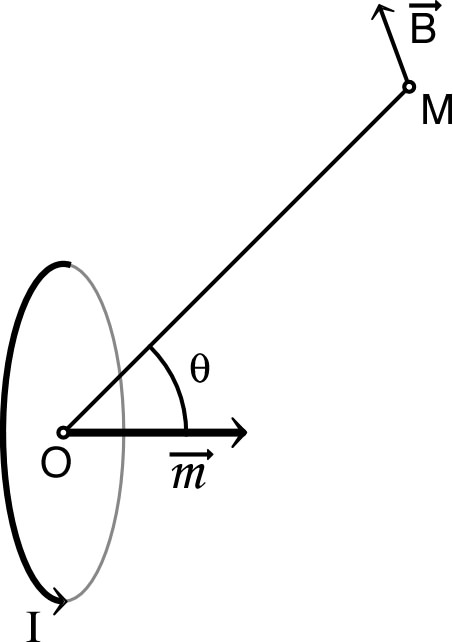
• On appelle “dipôle magnétique” un circuit électrique de type spire (mais non forcément circulaire) de dimension très petite en comparaison de la distance d’observation.

On appelle “moment dipolaire” le “vecteur”

\overset{→}{𝓂}=I \:\overset{→}{S}

(l’unité de base est

\mathrm{A.m^2}

) où

I

est le courant dans le circuit et

\overset{→}{S}

son (pseudo) “vecteur” surface (orienté selon le courant).

• Le champ magnétique d’une spire circulaire peut s’écrire sous une forme analogue à celle du dipôle électrostatique ; en coordonnées sphériques, d’axe

Oz

orienté selon

\overset{→}{S}

\overset{→}{B}=B_r (r,θ) \: \overset{→}{u}_r+B_θ (r,θ) \: \overset{→}{u}_θ

(d’après les symétries).

À grande distance :

\displaystyle B_r≈\frac{2 \,μ_0 \: 𝓂 \:\cos(θ)}{4π \:r^3}

\displaystyle B_θ≈\frac{μ_0 \: 𝓂 \:\sin(θ)}{4π \:r^3}

; correspondant à :

\displaystyle \overset{→}{B}=\frac{μ_0}{4π \:r^3} \: \left[3 \,(\overset{→}{𝓂}⋅\overset{→}{u}_r ) \: \overset{→}{u}_r-\overset{→}{𝓂} \,\right]

avec les lignes de champ suivantes.

◊ remarque : ces calculs ne sont toutefois valables que si la taille de la spire est très petite en comparaison de la distance “d’observation”

r=OM

; ils représentent en effet mal le champ à proximité du dipôle (ceci découle des différences fondamentales entre les propriétés de

\overset{→}{E}

\overset{→}{B}



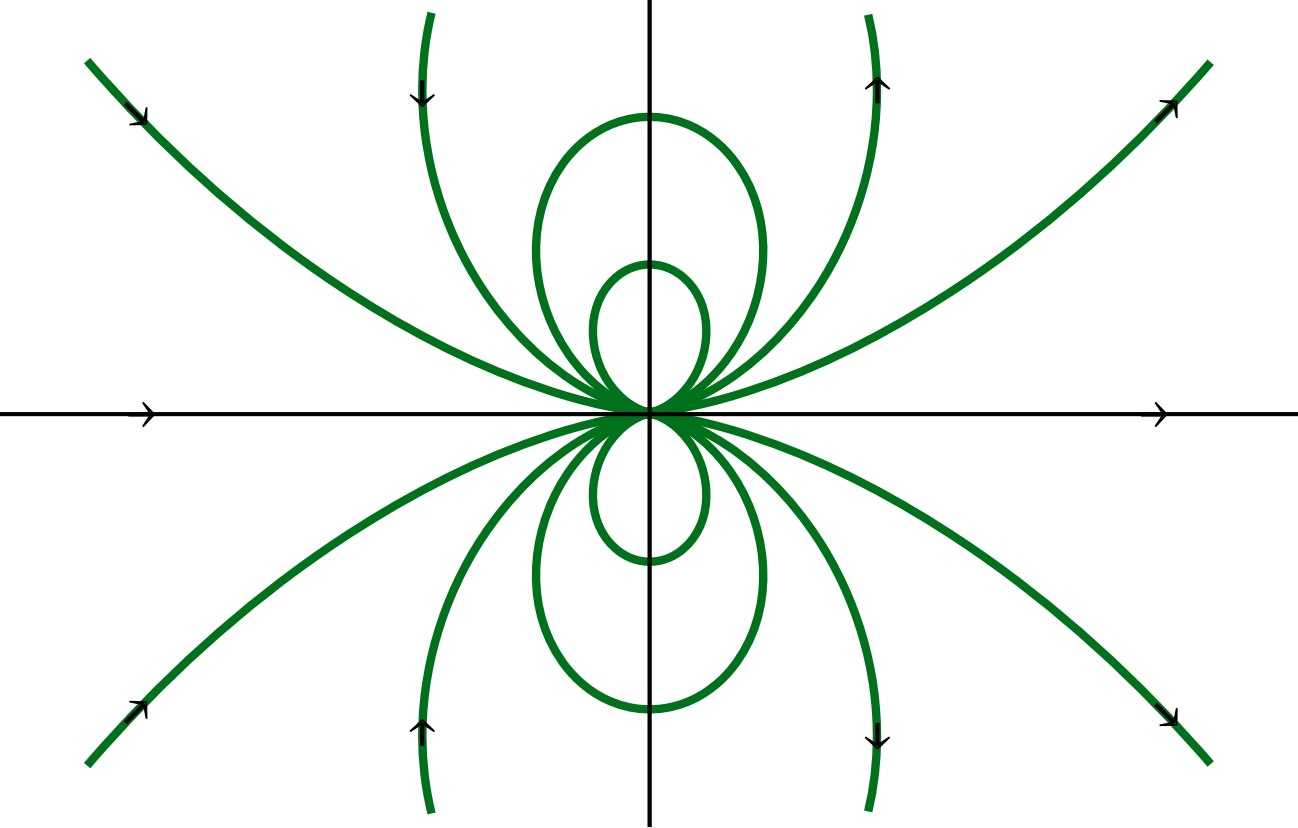
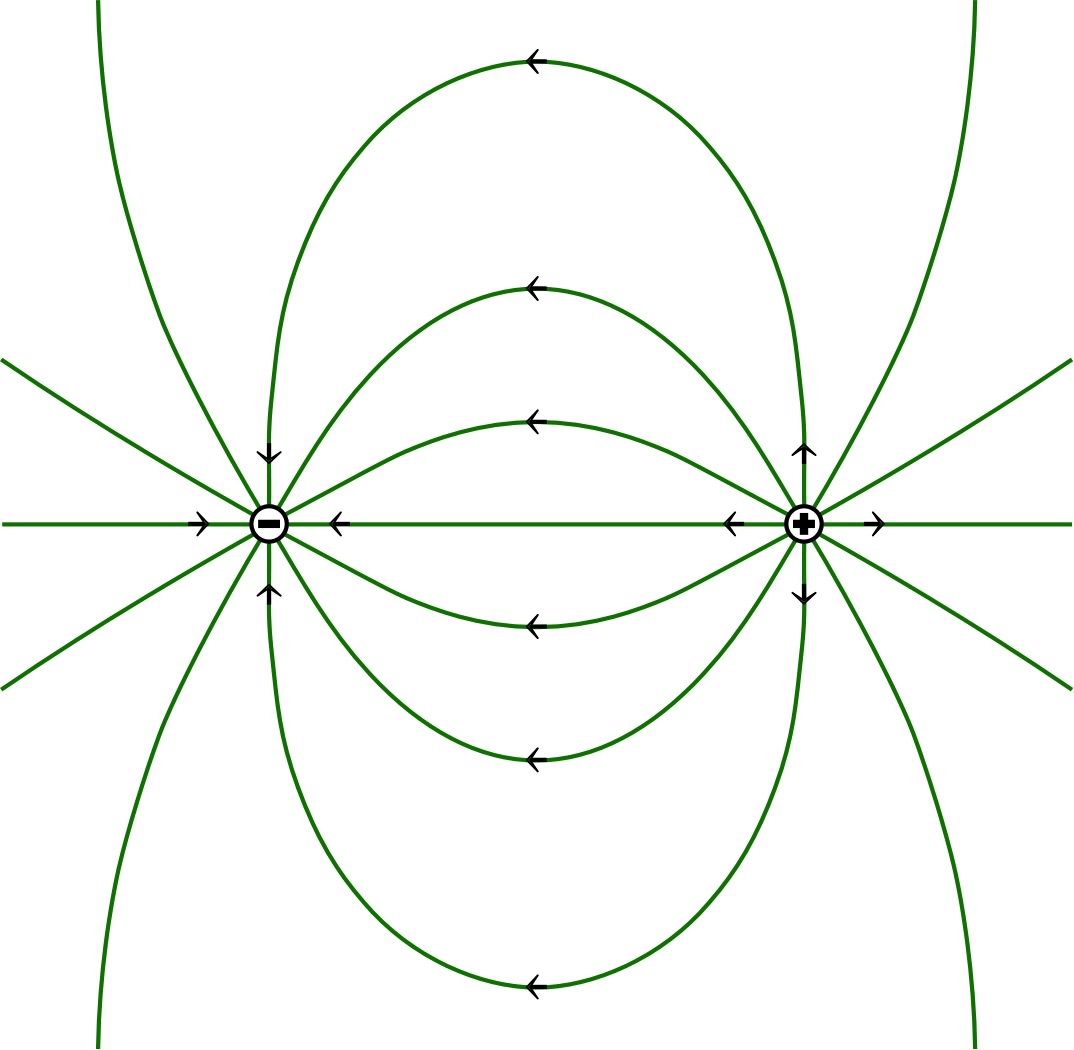dipôle électrostatique	dipôle magnétique

• De façon analogue au cas électrostatique, la principale action d’un champ

\overset{→}{B}

“extérieur” sur un dipôle est la tendance à l’orientation :

◊	la force totale est nulle si $\overset{→}{B}$ est uniforme ;

◊	il apparaît un moment de force, qui tend à aligner $\overset{→}{𝓂}$ selon le champ extérieur $\overset{→}{B}$ : $\overset{→}{ℳ}_O=\overset{→}{𝓂} × \overset{→}{B}$ .

◊ remarque : l’énergie potentielle du dipôle dans le champ extérieur peut s’écrire :

ℰ_p=-\overset{→}{𝓂}⋅\overset{→}{B}

; on vérifie ainsi que l’action du moment des forces tend à minimiser

ℰ_p

.

📖 exercice n° IV.