CHAMP MAGNÉTOSTATIQUE - corrigé des exercices


A. EXERCICES DE BASE

Bobines “façon Helmholtz”

1.a. • La spire est symétrique par rapport aux plans (Oxy)(Oxy) et (Oxz)(Oxz) , mais ces symétries retournent le sens du courant. Il s'agit d'antisymétries électriques donc de symétries magnétiques puisque le champ B→\overset{→}{B} est un pseudovecteur.
• En un point MM de l'axe (Ox)(Ox) , donc invariant dans ces symétries, le champ B→(M)\overset{→}{B}(M) doit être invariant. Il doit donc être symétrique par rapport à ces plans, donc parallèle à leur intersection (Ox)(Ox) .


1.b. • Le champ créé par un fil “infini” est orthoradial et de norme  B1=μ0I2πr\displaystyle B_1=\frac{μ_0 \: I}{2π \:r}  avec  r=x2+L2r=\sqrt{x^2+L^2} .
• Le champ créé par l'ensemble des deux fils est le double de la projection sur (Ox)(Ox) :
B(x)=2B1sin(α)=2B1Lr=μ0I2π2Lx2+L2\displaystyle B(x)=2 \,B_1 \; \sin(α)=2 \,B_1 \: \frac{L}{r}=\frac{μ_0 \: I}{2π} \, \frac{2 \,L}{x^2+L^2} .

magnStatique_cor_Im/magnStatique_cor_Im1.jpg
 magnStatique_cor_Im/magnStatique_cor_Im2.jpg


2. • En utilisant deux spires identiques mais centrées aux abscisses  ±a± a ,  on obtient sur l'axe un champ total :  B(x)=μ0ILπ(1(x+a)2+L2+1(x−a)2+L2)\displaystyle B(x)=\frac{μ_0 \: I \:L}{π} \: \left(\frac{1}{(x+a)^2+L^2}+\frac{1}{(x-a)^2+L^2}\right) .
• Puisque l'expression précédente est paire, on obtient la meilleure uniformité au voisinage de l'origine en y annulant la dérivée seconde :  d2Bdx2(0)=μ0ILπ2(3a2−L2)(a2+L2)2=0\displaystyle \frac{d^2 B}{{dx}^2} (0)=\frac{μ_0 \: I \:L}{π} \, \frac{2 \,(3 \,a^2-L^2 )}{(a^2+L^2 )^2} =0 .  La distance entre les bobines est alors  D=2a=2L3\displaystyle D=2 \,a=\frac{2 \,L}{\sqrt{3}} .
◊ remarque : le développement à l'origine peut alors s'écrire :  B(x)≈3μ0I2πL(1−916x4L4+⋯)\displaystyle B(x)≈\frac{3 \,μ_0 \: I}{2π \:L} \: \left(1-\frac{9}{16}\, \frac{x^4}{L^4} +⋯\right) .


3.a. • L'ensemble des deux spires est symétrique par rapport au plan (Oyz)(Oyz) et cette symétrie ne retourne pas le sens du courant. Il s'agit d'une symétrie électrique donc d'une antisymétrie magnétique puisque le champ B→\overset{→}{B} est un pseudovecteur.
• En un point MM de l'axe (Oy)(Oy) , donc invariant dans cette symétrie, le champ B→(M)\overset{→}{B}(M) doit être invariant. Il doit donc être antisymétrique par rapport à (Oyz)(Oyz) , donc perpendiculaire, c'est à dire selon (Ox)(Ox) .


3.b. • Le champ créé par un fil “infini” est orthoradial et de norme  B1=μ0I2πr\displaystyle B_1=\frac{μ_0 \: I}{2π \:r}  avec  r=a2+(L−y)2r=\sqrt{a^2+(L-y)^2} .
• Le champ créé par les deux fils avec courant de même sens est le double de la projection sur (Ox)(Ox) :
B(y)=2B1L−yr=μ0I2π2(L−y)a2+(L−y)2\displaystyle B(y)=2 \,B_1 \: \frac{L-y}{r}=\frac{μ_0 \: I}{2π} \, \frac{2 \,(L-y)}{a^2+(L-y)^2} .
• Le champ créé par les deux bobines est au total :  B(y)=μ0I2π(2(L−y)a2+(L−y)2+2(L+y)a2+(L+y)2)\displaystyle B(y)=\frac{μ_0 \: I}{2π} \, \left(\frac{2 \,(L-y)}{a^2+(L-y)^2}+\frac{2 \,(L+y)}{a^2+(L+y)^2}\right) .

magnStatique_cor_Im/magnStatique_cor_Im3.jpg
 magnStatique_cor_Im/magnStatique_cor_Im4.jpg


• Compte tenu de la valeur  a=L3\displaystyle a=\frac{L}{\sqrt{3}} ,  le développement en série à l'origine est de la même forme que celui obtenu selon (Ox)(Ox) :  B(y)≈3μ0I2πL(1−916y4L4+⋯)\displaystyle B(y)≈\frac{3 \,μ_0 \: I}{2π \:L} \: \left(1-\frac{9}{16}\, \frac{y^4}{L^4} +⋯\right) .  La représentation graphique montre que le champ est assez bien uniforme (à 5%5 % ) dans un intervalle de largeur  ≈L≈L , aussi bien selon (Oy)(Oy) que selon (Ox)(Ox) .


Champ magnétique créé par une hélice

1. ◊ remarque : en coordonnées cylindriques d'axe OzOz , l'équation correspondant à la coordonnée radiale est simplement  r=Rr=R  ;  il est en général difficile d'exprimer les coordonnées cylindriques d'un vecteur à partir des coordonnées de ses extrémités, mais ici le seul vecteur qui intervient est OM⟶\overset{⟶}{OM} ; par ailleurs, on ne peut pas intégrer simplement les composantes radiales et orthoradiales car les vecteurs unitaires u→r\overset{→}{u}_r et u→θ\overset{→}{u}_θ ne sont pas constants (ils dépendent du point MM considéré sur l'hélice), mais l'énoncé ne demande que la projection BzB_z ; rien n'interdirait donc ici d'utiliser les coordonnées cylindriques ; cependant, comme il s'agit d'un cas très particulier, on peut préférer étudier une méthode plus générale.
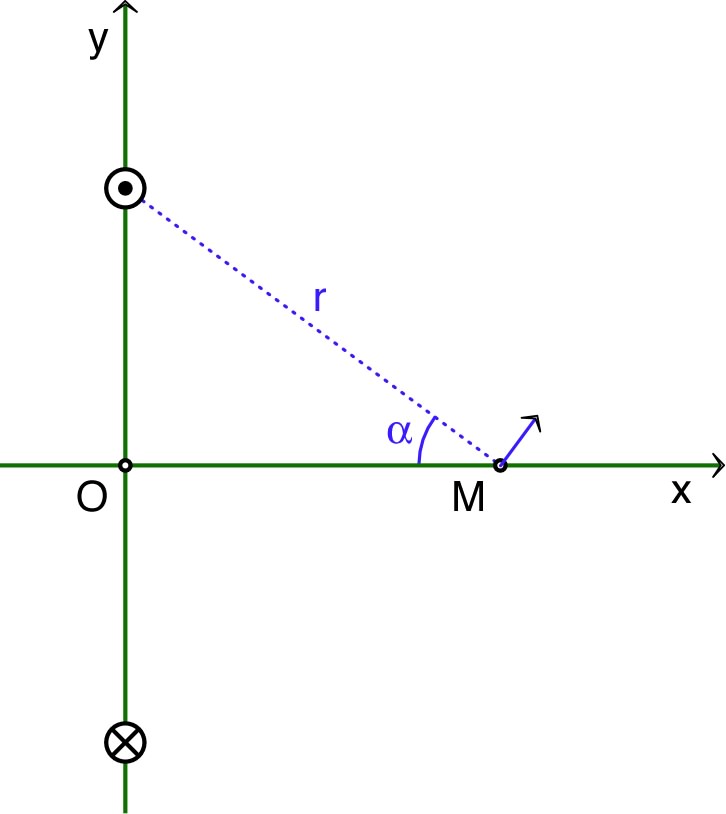
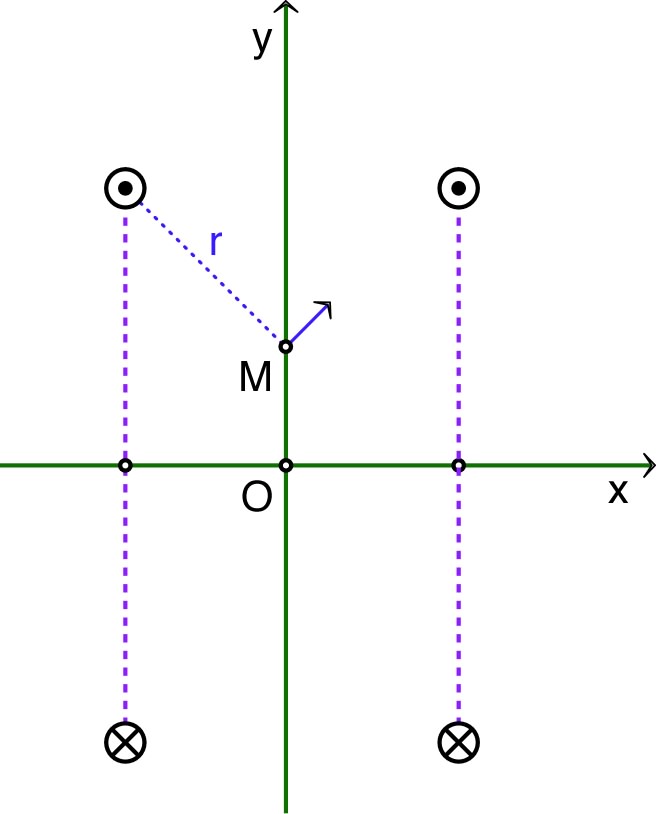
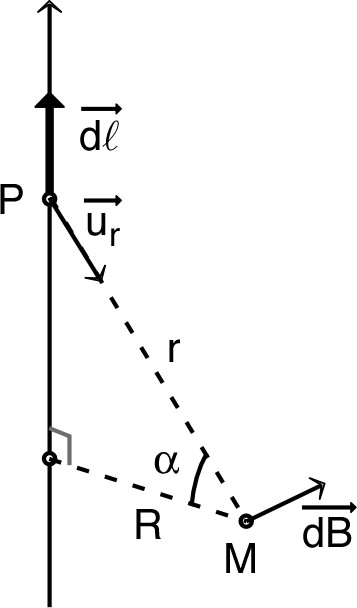
• On note MM un point quelconque de l'hélice ; d'après la loi de Biot et Savart, le champ en OO peut s'écrire :  B→=μ0I4π∫CdOM⟶×u→r′r′2\displaystyle \overset{→}{B}=\frac{μ_0 \: I}{4π} \, ∫_C \frac{d\overset{\longrightarrow}{OM} × \overset{→}{u}_r'}{{r'}^2}  avec  dOM⟶=dxu→x+dyu→y+dzu→zd\overset{\longrightarrow}{OM}=dx \:\overset{→}{u}_x+dy \:\overset{→}{u}_y+dz \:\overset{→}{u}_z  ;  r′=MO=R2+z2r'=MO=\sqrt{R^2+z^2}  ;  u→r′=MO⟶MO\displaystyle \overset{→}{u}_r'=\frac{\overset{\longrightarrow}{MO}}{MO} .
• Ainsi :  dOM⟶×MO⟶=(xu→x+yu→y+zu→z)×(dxu→x+dyu→y+dzu→z)d\overset{\longrightarrow}{OM}×\overset{\longrightarrow}{MO}=(x \:\overset{→}{u}_x+y \:\overset{→}{u}_y+z \:\overset{→}{u}_z)×(dx \:\overset{→}{u}_x+dy \:\overset{→}{u}_y+dz \:\overset{→}{u}_z)  donne en développant :
dOM⟶×MO⟶=(h2π[sin(θ)−θcos(θ)]u→x−h2π[cos(θ)+θsin(θ)]u→y+Ru→z)Rdθ\displaystyle d\overset{\longrightarrow}{OM}×\overset{\longrightarrow}{MO}=\left(\frac{h}{2π} \: [\sin(θ)-θ \:\cos(θ) ] \: \overset{→}{u}_x-\frac{h}{2π} \:[\cos(θ)+θ \:\sin(θ) ] \: \overset{→}{u}_y+R \:\overset{→}{u}_z \right) \: R \:dθ .
• En projetant l'intégrale vectorielle sur les vecteurs unitaires, on obtient :
Bx=μ0I4πRh2π∫−∞∞sin(θ)−θcos(θ)(R2+(hθ2π)2)3/2dθ\displaystyle B_x=\frac{μ_0 \: I}{4π} \, \frac{R \:h}{2π} \, ∫_{-∞}^∞ \:\frac{\sin(θ)-θ \:\cos(θ)}{\left(R^2+\left(\frac{h \:θ}{2π}\right)^2 \right)^{3/2}} \: dθ   ;   By=−μ0I4πRh2π∫−∞∞cos(θ)−θsin(θ)(R2+(hθ2π)2)3/2dθ\displaystyle B_y=-\frac{μ_0 \: I}{4π} \, \frac{R \:h}{2π} \, ∫_{-∞}^∞ \:\frac{\cos(θ)-θ \:\sin(θ)}{\left(R^2+\left(\frac{h \:θ}{2π}\right)^2 \right)^{3/2}} \: dθ  ;
Bz=μ0I4πR2∫−∞∞1(R2+(hθ2π)2)3/2dθ=μ0I4π2πhR2∫−∞∞1(R2+z2)3/2dz\displaystyle B_z=\frac{μ_0 \: I}{4π} \: R^2 \: ∫_{-∞}^∞ \:\frac{1}{\left(R^2+\left(\frac{h \:θ}{2π}\right)^2 \right)^{3/2}} \: dθ=\frac{μ_0 \: I}{4π} \, \frac{2π}{h} \: R^2 \, ∫_{-∞}^∞ \:\frac{1}{\left(R^2+z^2 \right)^{3/2}} \: dz .
◊ remarque : la composante ByB_y n'est pas simple à calculer (en coordonnées cylindriques, elle correspond à BrB_r puisque le point OO est sur l'axe), mais la composante BxB_x est nulle par symétrie : c'est l'intégrale d'une fonction impaire sur un intervalle symétrique (en coordonnées cylindriques, elle correspondrait à BθB_θ , dépourvue de signification en un point OO sur l'axe).
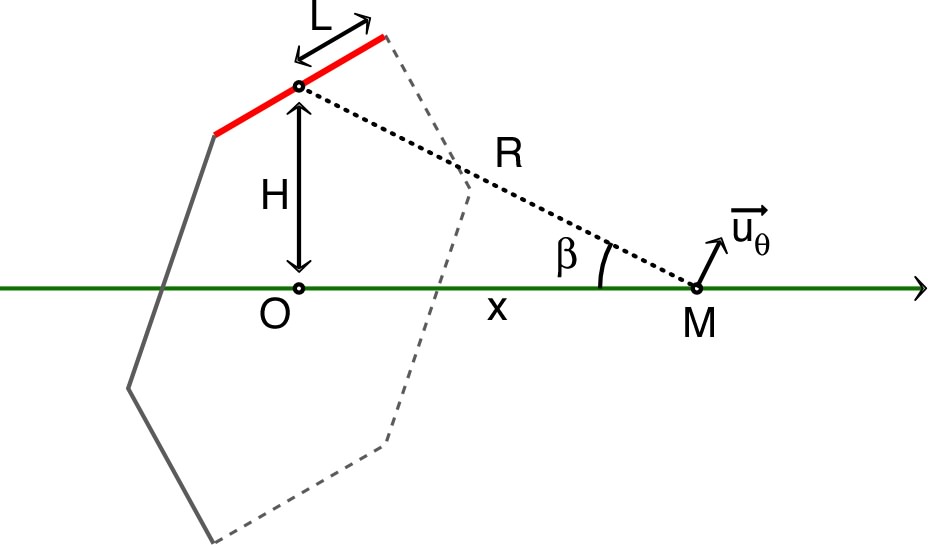
• Avec l'angle αα tel que  tan(θ)=zR\displaystyle \tan(θ)=\frac{z}{R}  on obtient :  Bz=μ0I2h∫−π/2π/2cos(α)dα=μ0Ih\displaystyle B_z=\frac{μ_0 \: I}{2 \,h} \, ∫_{-π/2}^{π/2} \cos(α) \: dα=\frac{μ_0 \: I}{h} .

2. • Puisque hh est le “pas” de l'hélice, c'est-à-dire la longueur du déplacement selon OzOz pour chaque tour, ceci correspond à un “nombre de spires par unité de longueur” :  n=1h\displaystyle n=\frac{1}{h}  (à cela près que si le pas est grand cela n'est qu'une “moyenne” délicate à interpréter).
• Pour  h≪Rh≪R  on retrouve par contre le champ magnétique du solénoïde infini :  Bz=μ0nIB_z=μ_0 \: n \:I .


Circuit polygonal

1.
• Pour calculer le champ créé par un circuit polygonal, on peut se ramener à calculer la contribution créée, par un segment de fil de longueur 2L2 \:L , en un point MM situé à une distance RR sur le plan médiateur.
• En coordonnées cylindriques par rapport au segment, puisque chaque contribution :  dB→=μ04πId𝓁→×u→rr2=μ0Id𝓁4πr2cos(α)u→θ\displaystyle d\overset{→}{B}=\frac{μ_0}{4π} \: \frac{I \:\overset{→}{d𝓁} × \overset{→}{u}_r}{r^2} =\frac{μ_0 \: I \:d𝓁}{4π \:r^2} \: \cos(α) \: \overset{→}{u}_θ  est perpendiculaire au plan défini par le fil et MM , alors il en est de même pour B→\overset{→}{B} total (selon u→θ\overset{→}{u}_θ ).
• En intégrant avec  r=R2+z2r=\sqrt{R^2+z^2}  ;  cos(α)=Rz\displaystyle \cos(α)=\frac{R}{z}  ;  z=Rtan(α)z=R \: \tan(α)  ;  d𝓁=dzd𝓁=dz  ;  λ=arctan(LR)\displaystyle λ=\arctan\left(\frac{L}{R}\right)  ;  on obtient :
dBθ=dB→⋅u→θ=μ0I4πd𝓁cos(α)r2\displaystyle dB_θ=d\overset{→}{B}⋅\overset{→}{u}_θ=\frac{μ_0 \: I}{4π} \, \frac{d𝓁 \:\cos(α)}{r^2}  ;
Bθ=μ0I4π∫−LLR(R2+z2)3/2dz=μ0I4π∫−λλcos(α)Rdα=μ0I2πRLR2+L2\displaystyle B_θ=\frac{μ_0 \: I}{4π} \, ∫_{-L}^L \: \frac{R}{\left(R^2+z^2 \right)^{3/2}} \: dz=\frac{μ_0 \: I}{4π} \, ∫_{-λ}^λ \frac{\cos(α)}{R} \: dα=\frac{μ_0 \: I}{2π \:R} \, \frac{L}{\sqrt{R^2+L^2}} .
magnStatique_cor_Im/magnStatique_cor_Im5.jpg

• En un point MM à l'abscisse xx sur l'axe du circuit polygonal, le champ est parallèle à cet axe compte tenu de l'invariance du circuit et de MM par rotation de 2πn\displaystyle \frac{2π}{n} (dans une rotation, un pseudo-vecteur se comporte comme un vecteur). Le champ total peut donc s'écrire  B→=Bxu→x\overset{→}{B}=B_x \: \overset{→}{u}_x  avec  Bx=nBθ(R)u→θ⋅u→xB_x=n \:B_θ (R) \; \overset{→}{u}_θ⋅\overset{→}{u}_x  où u→θ\overset{→}{u}_θ correspond aux coordonnées cylindriques par rapport au côté du polygone et où le calcul de RR peut être expliqué par un schéma sur un cas particulier (ici  n=6n=6 ) :

magnStatique_cor_Im/magnStatique_cor_Im6.jpg

• On obtient ainsi :  u→θ⋅u→x=sin(β)=HR=HH2+x2\displaystyle \overset{→}{u}_θ⋅\overset{→}{u}_x=\sin(β)=\frac{H}{R}=\frac{H}{\sqrt{H^2+x^2}}  avec  H=Lcot(πn)\displaystyle H=L \; \cot\left(\frac{π}{n}\right)  et au total :
Bx=nμ0I2πLH2+L2+x2HH2+x2\displaystyle B_x=n \: \frac{μ_0 \: I}{2π} \, \frac{L}{\sqrt{H^2+L^2+x^2}} \, \frac{H}{H^2+x^2} .

2. • Pour la limite  n→∞n→∞  on obtient :  L→0L→0  ;  nL→πR′n \:L→π \:R'  ;  H→R′H→R'  (rayon de la spire circulaire).
• On retrouve ainsi :  Bx→μ0I2R′2(R′2+x2)3/2\displaystyle B_x→\frac{μ_0 \: I}{2} \: \frac{{R'}^2}{\left({R'}^2+x^2 \right)^{3/2}} .


Dipôle magnétique

1. • On peut repérer le point MM par ses coordonnées sphériques avec un axe polaire selon l'axe de la spire. Le point MM et l'axe définissent un plan méridien (Orθ)(Orθ) qui est plan de symétrie de la spire, mais plan d'antisymétrie électrique.
• Puisque MM est invariant dans cette symétrie, le champ B→(M)\overset{→}{B}(M) doit être changé de sens. Or il s'agit d'un pseudovecteur ; il doit donc être parallèle au plan :  B→=Bru→r+Bθu→θ\overset{→}{B}=B_r \: \overset{→}{u}_r+B_θ \: \overset{→}{u}_θ .
• Enfin, la spire est invariante par rotation selon son axe ; lors d'une rotation d'angle φφ , le champ B→\overset{→}{B} tourne comme la base sphérique et ses coordonnées ne varient pas :  B→=Br(r,θ)u→r+Bθ(r,θ)u→θ\overset{→}{B}=B_r(r,θ) \: \overset{→}{u}_r+B_θ(r,θ) \: \overset{→}{u}_θ .

2. • D'après l'invariance par rotation d'angle φφ , on peut arbitrairement choisir  φ=0φ=0  pour le point MM . Soit PP un point de la spire, on peut le repérer par son angle noté ϕϕ .
• On obtient ainsi :
PM⟶=OM⟶−OP⟶=ru→r(θ)−Ru→R(ϕ)=r.(cos(θ)u→x+sin(θ)u→z)−R.(cos(ϕ)u→y+sin(ϕ)u→z)\overset{⟶}{PM}=\overset{⟶}{OM}-\overset{⟶}{OP}=r \:\overset{→}{u}_r (θ)-R \:\overset{→}{u}_R (ϕ)=r.(\cos(θ) \:\overset{→}{u}_x+\sin(θ) \:\overset{→}{u}_z )-R.(\cos(ϕ) \:\overset{→}{u}_y+\sin(ϕ) \:\overset{→}{u}_z )  ;
PM2=r2+2rRu→r⋅u→R+R2=r2+2rRsin(θ)sin(ϕ)+R2{PM}^2=r^2+2 \,r \:R \:\overset{→}{u}_r⋅\overset{→}{u}_R+R^2=r^2+2 \,r \:R \: \sin(θ) \, \sin(ϕ)+R^2  ;
d𝓁→=Rdϕu→ϕ(ϕ)=Rdϕ.(cos(ϕ)u→z−sin(ϕ)u→y)\overset{→}{d𝓁}=R \:dϕ \;\overset{→}{u}_ϕ (ϕ)=R \:dϕ .(\cos(ϕ) \: \overset{→}{u}_z-\sin(ϕ) \: \overset{→}{u}_y )  ;
d𝓁→×PM⟶=rRdϕ.(−sin(ϕ)sin(θ)u→x+cos(ϕ)cos(θ)u→y+sin(ϕ)cos(θ)u→z)+R2dϕu→x\overset{→}{d𝓁} × \overset{⟶}{PM}=r \:R \:dϕ .\left(-\sin(ϕ) \, \sin(θ) \:\overset{→}{u}_x+\cos(ϕ) \, \cos(θ) \: \overset{→}{u}_y+\sin(ϕ) \, \cos(θ) \: \overset{→}{u}_z \right)+R^2 \: dϕ \;\overset{→}{u}_x  ;
dB→=μ0I4πd𝓁→×PM⟶PM3≈μ0I4πr3(1−3Rrsin(θ)sin(ϕ))d𝓁→×PM⟶\displaystyle d\overset{→}{B}=\frac{μ_0 \: I}{4π} \, \frac{\overset{→}{d𝓁} × \overset{⟶}{PM}}{{PM}^3} ≈\frac{μ_0 \: I}{4π \:r^3} \: \left(1-\frac{3 \,R}{r} \: \sin(θ) \, \sin(ϕ) \right) \: \overset{→}{d𝓁} × \overset{⟶}{PM}  ;
d𝓁→×PM⟶⋅u→r=R2cos(θ)dϕ\overset{→}{d𝓁} × \overset{⟶}{PM}⋅\overset{→}{u}_r=R^2 \: \cos(θ) \: dϕ  ;
d𝓁→×PM⟶⋅u→θ=(rRsin(ϕ)−R2sin(θ))dϕ\overset{→}{d𝓁} × \overset{⟶}{PM}⋅\overset{→}{u}_θ=(r \:R \:\sin(ϕ)-R^2 \: \sin(θ) ) \: dϕ  ;
Br=μ0I4πr3R2cos(θ)(2π+3Rrsin⁡(θ)∫sin(ϕ)dϕ)=μ0I4πr32Scos(θ)=μ0𝓂4πr32cos(θ)\displaystyle B_r=\frac{μ_0 \: I}{4π \:r^3} \: R^2 \: \cos(θ) \: \left(2π+\frac{3 \:R}{r} \, sin⁡(θ) \, ∫ \,\sin(ϕ) \: dϕ\right)=\frac{μ_0 \: I}{4π \:r^3} \: 2 \,S \: \cos(θ)=\frac{μ_0 \: 𝓂}{4π \:r^3} \: 2 \, \cos(θ)  ;
Bθ=−μ0I4πr3R2sin(θ)(2π−3∫sin2(ϕ)dϕ)=μ0I4πr3Ssin(θ)=μ0𝓂4πr3sin(θ)\displaystyle B_θ=-\frac{μ_0 \: I}{4π \:r^3} \: R^2 \: \sin(θ) \: \left(2π-3 \,∫ \sin^2(ϕ) \: dϕ\right)=\frac{μ_0 \: I}{4π \:r^3} \: S \:\sin(θ)=\frac{μ_0 \: 𝓂}{4π \:r^3} \: \sin(θ) .


B. EXERCICE D’APPROFONDISSEMENT

Expérience de Rowland


 • La quantité de charge portée par un anneau entre  rr  et  r+drr+dr  est  dq=σdS=σ2πrdrdq=σ \:dS=σ \:2π \:r \:dr .
• Cette charge fait un tour en une durée  T=2πω\displaystyle T=\frac{2π}{ω}  ;  ceci correspond à un courant :  dI=dqT=σωrdr\displaystyle dI=\frac{dq}{T}=σ \:ω \:r \:dr .
• Sur l'axe d'une spire circulaire de rayon rr , parcourue par un courant dIdI , à une distance  aa  du centre, le champ magnétique est parallèle à l'axe et a pour norme :  dB=μ0dIr22(r2+a2)3/2\displaystyle dB=\frac{μ_0 \: dI \:r^2}{2 \,\left(r^2+a^2 \right)^{3/2}} .
• Le champ magnétique total a donc pour norme :  B=μ0σω2∫0Rr3(r2+a2)3/2dr\displaystyle B=\frac{μ_0 \: σ \:ω}{2} \, ∫_0^R \frac{r^3}{\left(r^2+a^2 \right)^{3/2}} \: dr .
• On peut alors considérer :
2R′=∫0R2r3(r2+a2)3/2dr=∫a2a2+R2duu−a2∫a2a2+R2duu3/2\displaystyle 2 \,R'=∫_0^R \frac{2 \,r^3}{\left(r^2+a^2 \right)^{3/2}} \: dr=∫_{a^2}^{a^2+R^2} \frac{du}{\sqrt{u}} \;-\; a^2 \,∫_{a^2}^{a^2+R^2} \frac{du}{u^{3/2}}  ;
R′=(a2+R2−a)+a2.(1a2+R2−1a)=16,3cm\displaystyle R'=\left(\sqrt{a^2+R^2}-a\right)+a^2.\left(\frac{1}{\sqrt{a^2+R^2}}-\frac{1}{a}\right)=16\text{,}3 \:\mathrm{cm}  ;
B=μ0σω2R′\displaystyle B=\frac{μ_0 \: σ \:ω}{2} \: R' .
• Pour des plaques très proches, on peut modéliser par des plans infinis ; le champ électrique entre les plaques est alors uniforme et de norme :  E=σε0\displaystyle E=\frac{σ}{ε_0}  .  La tension est par ailleurs :  U=EdU=E \:d ,  d'où la densité de charges  σ=ε0Ud\displaystyle σ=\frac{ε_0 \: U}{d}  et (compte tenu de la relation  ε0μ0c2=1ε_0 \: μ_0 \: c^2=1 )  le champ magnétique  B=Uω2dc2R′\displaystyle B=\frac{U \:ω}{2 \,d \:c^2} \: R' .
• On obtient ainsi :  B=4,3.10−10T≪B0B=4\text{,}3.{10}^{-10} \: \mathrm{T}≪B_0 .