CHAMP MAGNÉTOSTATIQUE - exercices

A. EXERCICES DE BASE

Bobines “façon Helmholtz”

• Une “spire” rectangulaire de centre $O$ , comportant $N$ tours de fil, est parcourue par un courant $I$ . Sa longueur  $2 \,L'$  selon l'axe $(Oz)$ est très supérieure à sa largeur $2 \,L$ selon l'axe $(Oy)$ , de telle sorte qu'on peut la modéliser par une paire de fils rectilignes “infinis” parcourus par des courants de sens contraires.

a) D'après les symétries, déterminer l'orientation du champ magnétique en un point $M$ de l'axe $(Ox)$ .

b) Calculer le champ magnétique algébrique $B(x)$ en $M$ . Tracer la courbe représentative de $B(x)$ .

• En déduire qu’en associant deux spires identiques, de même axe, dont les centres sont à une distance $D$ l’un de l’autre, judicieusement choisie, on obtient un champ pratiquement uniforme dans une région de l’espace à préciser.

• On considère un assemblage de deux spires, à la distance $D$ déterminée précédemment.

a) D'après les symétries, déterminer l'orientation du champ magnétique en un point $M$ de l'axe $(Oy)$ .

b) Calculer le champ magnétique algébrique $B(y)$ en $M$ . Tracer la courbe représentative de $B(y)$ . Commenter.

Champ magnétique créé par une hélice

• Une hélice de rayon  $R$  et de pas  $h$  a pour équations cartésiennes paramétriques (dans un repère orthonormé) :  $x=R \; \cos(θ)$  ;  $y=R \; \sin(θ)$  ;  $\displaystyle z=\frac{h \:θ}{2π}$  ;  où le paramètre $θ$ varie de $-∞$ à $+∞$ . Cette hélice est parcourue par un courant $I$ .

• À l’aide de la loi de Biot et Savart, calculer la coordonnée $B_z$ du champ magnétique en $O$ .

• Montrer que pour  $h≪R$  on retrouve le champ magnétique du solénoïde infini.

Circuit polygonal

• Soit un circuit en forme de polygone régulier à $n$ côtés, parcouru par un courant $I$ . Calculer le champ magnétique créé par ce circuit en un point $M$ quelconque sur l’axe.

• Vérifier qu'on retrouve le champ créé par une spire circulaire pour la limite  $n→∞$ .

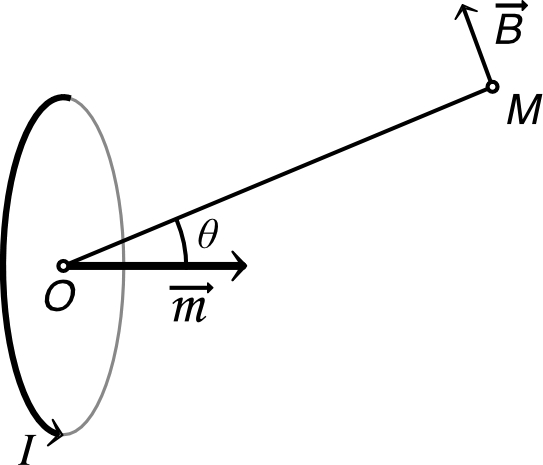
Dipôle magnétique

• Soit un circuit circulaire parcouru par un courant $I$ , étudié en coordonnées sphériques. À l'aide des symétries, montrer que son champ magnétique peut s'écrire sous la forme :  $\overset{→}{B}=B_r (r,θ) \: \overset{→}{u}_r+B_θ (r,θ) \: \overset{→}{u}_θ$ . • Calculer ce champ magnétique à grande distance, dans l'approximation dipolaire.

B. EXERCICE D’APPROFONDISSEMENT

Expérience de Rowland

• On considère un condensateur plan dont les armatures, distantes de  $d=1 \:\mathrm{cm}$ , sont des disques métalliques de rayon  $R=20 \:\mathrm{cm}$  (munis “d’anneaux de garde”, pour limiter les “effets de bord”). L’une des armatures est fixe, l’autre est animée d’un mouvement de rotation uniforme autour de son axe, à la vitesse angulaire  $ω=125 \:\mathrm{tr.s^{-1}}$  ;  la différence de potentiel entre les armatures est  $U=6\text{,}0.{10}^3 \: \mathrm{V}$ .

• En supposant que les charges sont entraînées par le mouvement, sans modification de leur répartition, calculer le champ magnétique créé sur l’axe, à la distance  $a=2 \:\mathrm{cm}$  du centre de l’armature en rotation.

◊ remarque : cette expérience (1876) avait pour but de montrer que le courant électrique est bien lié à un mouvement de charges ; sa réalisation est particulièrement délicate : il suffit de comparer le champ magnétique ainsi produit à la composante horizontale du champ magnétique terrestre  $B_0≈2.{10}^{-5} \: \mathrm{T}$ .