sp. I - OSCILLATEURS

1. Notion d'oscillateur harmonique

1.1. Exemple de l'oscillateur mécanique sans frottement

• On considère un oscillateur à ressort horizontal sans frottement.

La réaction normale $\overrightarrow{R}$ du support compense le poids $\overrightarrow{P}$ (mouvement horizontal).

• En choisissant comme origine la position d'équilibre, on en déduit l’équation différentielle :  $m \:\ddot{x}=-k \:x$  ;  ce qui peut encore s’écrire :  $\ddot{x }+ω_0^{\:2} \:x=0$  avec la pulsation  $ω_0=\sqrt{\frac{k}{m}}$ .

1.2. Généralisation

• On considère un point matériel dont l’énergie potentielle dépend d’une variable de position $x$.

Pour les cas “usuels”, on peut montrer qu'au voisinage de “toute” position $X$ il est possible d'exprimer l'énergie potentielle sous forme d'un développement en série, donc les termes sont de plus en plus petits si  $x-X$  est petit :
        $E_p \left(x\right)=E_p \left(X\right)+\left(x-X\right) \:\frac{dE_p}{dx} \left(X\right)+\frac{1}{2} \left(x-X\right)^2 \:\frac{d^2 E_p}{dx^2} \left(X\right)+⋯$

Une position d’équilibre stable en $x_e$ correspond à un minimum de $E_p$ ; ainsi au voisinage d’une position d’équilibre stable :  $E_p \left(x\right)≈E_p \left(x_e \right)+\frac{K}{2} \left(x-x_e \right)^2$  où le coefficient  $K=\frac{d^2 E_p}{dx^2} \left(x_e \right)>0$  est nommé “raideur” de l’oscillateur.

• Le point est soumis à une force “de rappel” de coordonnée (algébrique) :  $F_x=-\frac{dE_p}{dx} \left(x\right)=-K.\left(x-x_e \right)$  (correspondant à la loi de Hooke).

En prenant pour simplifier l'origine à la position d'équilibre  ($x_e=0$),  le mouvement au voisinage de l'équilibre est décrit par l’équation :  $\ddot{x}+ω_0^{\:2} \:x=0$  avec la pulsation  $ω_0=\sqrt{\frac{K}{m}}$  .

◊ remarque : le raisonnement peut se généraliser à des cas où la variable $x$ n'est pas une longueur (variable angulaire, électrique...).

2. Caractéristiques du mouvement

• Les solutions de :  $\ddot{x}+ω_0^{\:2} \:x=0$  sont de la forme :  $x=X_m \:\cos⁡\left(ω_0 \:t+φ\right)$  où l'amplitude $X_m$ et le “déphasage” (ou “phase initiale”) $φ$ sont des constantes d’intégration déterminées par les “conditions aux limites”.

Par exemple si on impose des conditions initiales $x\left(0\right)$ et $\dot{x }\left(0\right)$ :
        $X_m=\sqrt{{x\left(0\right)}^2+\frac{{\dot{x}\left(0\right)}^2}{ω_0^{\:2}}}$  ;  $X_m \:\cos⁡\left(φ\right)=x\left(0\right)$  ;  $X_m \:\sin⁡\left(φ\right)=-\frac{\dot{x}(0)}{ω_0}$  .

◊ remarque : on peut aussi utiliser :  $x=A \:\cos⁡\left(ω_0 \,t\right)+B \:\sin⁡\left(ω_0 \,t\right)$  ;  les conditions initiales imposent alors :  $A=x\left(0\right)$  et  $B=\frac{\dot{x}\left(0\right)}{ω_0}$  .

◊ remarque : pour une équation différentielle linéaire, toute combinaison linéaire de solutions et/ou de leurs dérivées est aussi solution.

• La période  $T_0=\frac{2π}{ω_0}$   ne dépend pas de l’amplitude des oscillations tant que celle-ci est assez faible pour qu’on puisse négliger les termes supérieurs du développement de $E_p \left(x\right)$  (propriété d’isochronisme des “petites” oscillations).

• L’énergie cinétique est :  $E_c=\frac{1}{2} m \:\dot{x}^2=\frac{1}{2} m \:ω_0^{\:2} \:X_m^{\:2} \:\sin^2⁡\left(ω_0 \,t+φ\right)$  ;  l’énergie potentielle peut s'écrire :  $E_p=\frac{1}{2} K \:x^2=\frac{1}{2} m \:ω_0^{\:2} \:X_m^{\:2} \:\cos^2⁡\left(ω_0 \,t+φ\right)$  ;  on retrouve ainsi que  $E_m=E_c+E_p=\frac{1}{2} m \:ω_0^{\:2} \:X_m^{\:2}$  est constante.

On peut aussi écrire plus généralement :  $\dot{E}_m=\dot{E}_c+\dot{E}_p=m \:\ddot{x} \:\dot{x}+K \:x \:\dot{x}=m \:\dot{x} \;\left(\ddot{x}+ω_0^{\:2} \:x\right)=0$ .

3. Représentation de Fresnel

• Les variations d'un signal de la forme :  $x=X_m \:\cos⁡\left(ω_0 \,t+φ\right)$  peuvent être représentées à l'aide d'un vecteur $\overrightarrow{X_m}$ de norme $X_m$ tournant à la vitesse angulaire $ω_0$.

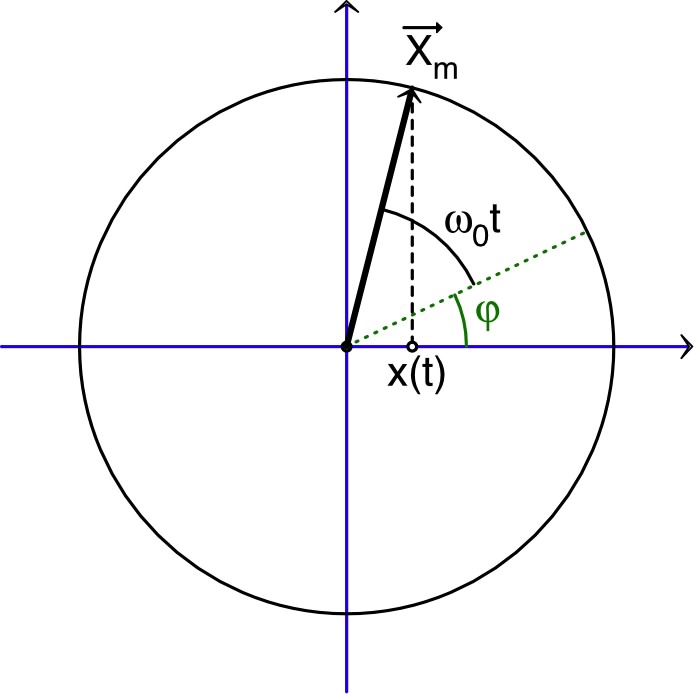
◊ remarque : le vecteur dérivé, tourné de $\frac{π}{2}$ ,  représente aussi le signal dérivé :
        $\dot{x}=-ω_0 \:X_m \:\sin⁡\left(ω_0 \,t+φ\right) =ω_0 \:X_m \:\cos⁡\left(ω_0 \,t+φ+\frac{π}{2}\right)$.

◊ remarque : cela peut donc aussi être noté à l'aide des nombres complexes ; la projection horizontale correspond à la partie réelle.

📖 exercices n° I, II, III

4. Décomposition de Fourier

• On peut montrer que “tout” signal périodique “centré” de fréquence $F$ peut être décomposé (équivalent à) une superposition de signaux sinusoïdaux de fréquences  $n \:F$,  avec  $n∈ℕ$  (“série de Fourier”).

La fréquence $F$ est appelée “fondamentale” et les autres “harmoniques”. La répartition des amplitudes des composantes est appelée “spectre de Fourier”.

◊ remarque : ceci se généralise pour les signaux non périodiques, en superposant des sinusoïdes de toutes les fréquences (“transformée de Fourier”).

• Dans de nombreuses circonstances (au moins pour les faibles amplitudes), le comportement des signaux est décrit par des équations différentielles linéaires. La connaissance du comportement des composantes sinusoïdales de Fourier suffit donc à connaître celui d'un signal quelconque.

• Les ordres de grandeur usuels dépendent des types de signaux :

	◊ 1 à 10 Hz pour les ondes sismiques ;
	◊ 20 à 20000 Hz pour les ondes sonores (audibles) ;
	◊ 400 à 800 THz (1012 Hz) pour les ondes lumineuses (visibles).