OSCILLATEURS - exercices


A. EXERCICES DE BASE

I. Suspension des voitures

        • Les oscillations du dispositif de suspension des voitures sont plus facilement supportables si elles correspondent à une période à laquelle l'organisme est habitué : la période de la marche, qui est  T≈0,8sT≈0,8 \:\mathrm{s}.  Calculer de combien s'abaisse une voiture de masse  M=1500kgM=1500\: \mathrm{kg}  lorsqu'on y introduit une malle de 70kg70 \:\mathrm{kg}. Expliquer pourquoi un camion ne peut pas être confortable.


II. Conditions aux limites

        • On considère un oscillateur harmonique de période  T0=2,0sT_0=2,0 \:\mathrm{s}  décrit par une position x(t)x\left(t\right) mesurée par rapport à la position d'équilibre.
        • Sa vitesse initiale est :  x˙(0)=1,0m.s−1\dot{x}\left(0\right)=1,0 \:\mathrm{m.s^{-1}}  ;  sa position lors de la première annulation de la vitesse est :  x1=0,5mx_1=0,5 \:\mathrm{m} .

1.     • Préciser l'équation horaire sous la forme :  x(t)=Xmcos⁡(ω0t+φ)x\left(t\right)=X_m \:\cos⁡\left(ω_0 \,t+φ\right) .

2.     • Préciser l'équation horaire sous la forme :  x(t)=Acos⁡(ω0t)+Bsin⁡(ω0t)x\left(t\right)=A\:\cos⁡\left(ω_0 \,t\right) + B \:\sin⁡\left(ω_0 \,t\right) .


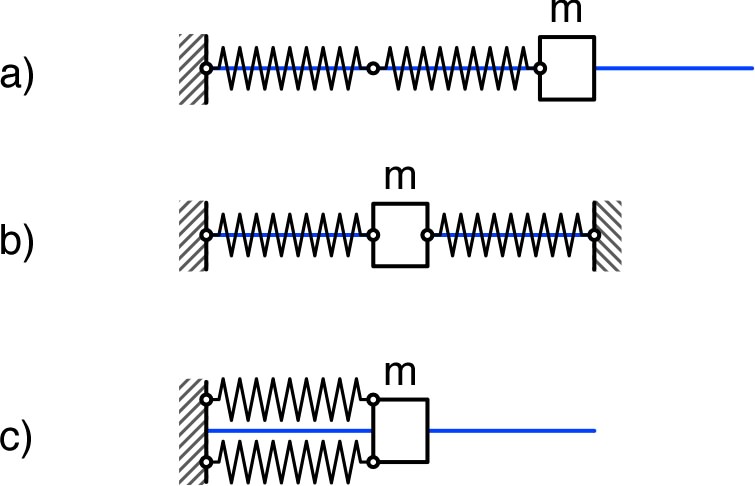
III. Associations de ressorts

        • Une masse mm, mobile sans frottement sur un axe Ox Ox horizontal, est reliée à deux ressorts de masse négligeable, de longueurs “à vide” 𝓁01𝓁_01 et 𝓁02𝓁_02 et de raideurs k1k_1 et k2k_2 .
        • Déterminer la période des oscillations pour les trois montages ci-après.

Oscillateurs_ex_Im/Oscillateurs_ex_Im1.jpg



B. EXERCICE D’APPROFONDISSEMENT

IV. Grandes oscillations du pendule pesant

        • On cherche les corrections à apporter à la solution approchée de l'équation :   θ̈+ω02sin⁡(θ)=0\ddot{θ}+ω_0^{\:2} \:\sin⁡\left(θ\right)=0  quand l'amplitude du mouvement est trop grande pour confondre  θθ  et  sin⁡(θ)\sin⁡\left(θ\right).

1.     • Écrire l'équation différentielle en développant sin⁡(θ)\sin⁡\left(θ\right) jusqu'au premier terme non nul suivant l'ordre 1.

2.     • Chercher une solution approchée de cette équation, sous la forme :  θ=θ0[sin⁡(ωt)+εsin⁡(3ωt)]θ= θ_0 \:\left[\sin⁡\left(ω\,t\right)+ε \:\sin⁡\left(3ω \,t\right) \right]   avec  ε≪1ε≪1 .  Exprimer ωω en fonction de ω0ω_0 et θ0θ_0 ; en déduire l'expression correspondante pour la période TT.

3.     • Exprimer εε en fonction de θ0θ_0  (ce coefficient détermine l'importance de la fréquence “harmonique” 3ω3ω dans le développement limité le l'expression décrivant le mouvement).