SIGNAUX PÉRIODIQUES - corrigé du TP

1. Utilisation d'un oscilloscope en voltmètre

1.1. Mode alternatif ; influence de l’amplitude

• En mode alternatif, les voltmètres peuvent mesurer la valeur efficace du signal, c’est-à-dire la racine carrée de la moyenne du carré :  $U_{eff}=\sqrt{\frac{∫_0^T \:{u\left(t\right)}^2 dt}{∫_0^T\:dt}}$ .

Pour un signal sinusoïdal  $u\left(t\right)=U_m \:\sin⁡\left(ω \,t\right)$  on obtient ainsi :  $U_{eff}=U_m \:\sqrt{ \left⟨\sin^2⁡\left(ω \,t\right) \right⟩}$ .  Mais pour les intégrales sur une période, les fonctions sinus et cosinus sont juste décalées dans le temps, donc elles sont égales :  $∫_0^T \:\sin^2⁡\left(ω \,t\right) \:dt=∫_0^T \:\cos^2⁡\left(ω \,t\right) \:dt$  ;  en outre  $\sin^2⁡\left(ω \,t\right)+\cos^2⁡\left(ω \,t\right)=1$  donc la valeur commune de ces deux intégrales est :  $∫_0^T \:\sin^2⁡\left(ω \,t\right) \:dt=\frac{1}{2} \:∫_0^T\:dt=\frac{T}{2}$ .  On obtient donc :  $\left⟨\sin^2⁡\left(ω \,t\right) \right⟩=\frac{1}{2}$  et  $U_{eff}=\frac{U_m}{\sqrt{2}}$ .

Pour un signal triangulaire, en calculant sur une demi-période seulement (par symétrie), on peut écrire :  $u\left(t\right)=α \:t$  avec  $α \,\frac{T}{4}=U_m$ .  On obtient ainsi :  $U_{eff}=α \:\sqrt{\left⟨t^2 \right⟩}$ .  Or, pour les intégrales sur une demi-période :  $∫_{-T⁄4}^{T/4} \:t^2 \:dt=\frac{2}{3} \left(\frac{T}{4}\right)^3$.  On obtient donc :  $\left⟨t^2 \right⟩=\frac{T^2}{48}$  et  $U_{eff}=\frac{U_m}{\sqrt{3}}$ .

• Expérimentalement, on étudie d’abord des signaux sinusoïdaux de fréquence  $50,0±0,4 \:\mathrm{Hz}$  pour lesquels sont prévus les multimètres.

On vérifie que la tension de décalage $U_d$ du signal est négligeable en comparaison de l’amplitude $U_m$ (on mesure $U_{m1}$ sur l’écran de l’oscilloscope et $U_{m2}$ avec le multimètre intégré à l’oscilloscope).

$U_d \;\left⟦\mathrm{V}\right⟧$	$U_{m1} \;\left⟦\mathrm{V}\right⟧$	$U_{m2} \;\left⟦\mathrm{V}\right⟧$	$\frac{U_m}{\sqrt{2}} \;\left⟦\mathrm{V}\right⟧$	$U_{eff1} \;\left⟦\mathrm{V}\right⟧$	$U_{eff2} \;\left⟦\mathrm{V}\right⟧$
$0,02±0,02$	$1,00±0,04$	$1,03±0,03$	$0,721±0,022$	$0,711±0,004$	$0,740±0,044$
$-0,03±0,03$	$3,00±0,11$	$3,06±0,07$	$2,150±0,049$	$2,117±0,013$	$2,160±0,091$

On compare ensuite $\frac{U_m}{\sqrt{2}}$ et les valeurs efficaces $U_{eff}$ indiquées par deux multimètres en mode alternatif (la deuxième avec celui intégré à l’oscilloscope).

Les écarts constatés sont comparables aux incertitudes de mesure (assez grandes pour l’oscilloscope), ce qui semble confirmer la relation entre l’amplitude $U_m$ et la valeur efficace $U_{eff}$.

• On étudie ensuite de même des signaux triangulaires.

$U_d \;\left⟦\mathrm{V}\right⟧$	$U_{m1} \;\left⟦\mathrm{V}\right⟧$	$U_{m2} \;\left⟦\mathrm{V}\right⟧$	$\frac{U_m}{\sqrt{3}} \;\left⟦\mathrm{V}\right⟧$	$U_{eff1} \;\left⟦\mathrm{V}\right⟧$	$U_{eff2} \;\left⟦\mathrm{V}\right⟧$
$-0,02±0,02$	$1,00±0,04$	$1,03±0,03$	$0,589±0,017$	$0,581±0,003$	$0,620±0,043$
$-0,03±0,03$	$3,00±0,11$	$3,06±0,07$	$1,755±0,041$	$1,727±0,009$	$1,800±0,089$

On compare alors $\frac{U_m}{\sqrt{3}}$ et les valeurs efficaces $U_{eff}$ indiquées par deux multimètres en mode alternatif  (la deuxième avec celui intégré à l’oscilloscope).

Les écarts constatés sont comparables aux incertitudes de mesure (assez grandes pour l’oscilloscope), ce qui semble confirmer la relation entre l’amplitude $U_m$ et la valeur efficace $U_{eff}$.

◊ remarque : ceci montre que la mesure effectuée est dans les deux cas la valeur efficace “vraie” (et non simplement l’amplitude divisée par $\sqrt{2}$ ).

1.2. Mode alternatif ; influence d’une tension de décalage

• On ajoute ensuite une composante continue aux signaux alternatifs afin de savoir si les multimètres  utilisés (en mode alternatif) filtrent ou non la partie alternative avant de mesurer la valeur efficace.

Pour un signal sinusoïdal décalé  $u\left(t\right)=U_d+U_m \:\sin⁡\left(ω \,t\right)$  on obtient encore ainsi  $U_e=\frac{U_m}{\sqrt{2}}$  si l’appareil filtre la partie alternative avant de la mesurer, mais dans le cas contraire on obtient :
        $\left⟨u\left(t\right)^2 \right⟩= U_d^{\:2} + 2 \:U_d \:U_m \:\left⟨\sin⁡\left(ω \,t\right) \right⟩+U_m^{\:2} \:\left⟨\sin^2⁡\left(ω \,t\right) \right⟩=U_d^{\:2}+U_e^{\:2}$
c’est-à-dire que la valeur efficace est :  $U_{eff}=\sqrt{U_d^{\:2}+U_e^{\:2}}$  supérieure à $U_d$ et à $U_e$ mais inférieure à  $U_d+U_e$ .

Pour un signal triangulaire décalé  $u\left(t\right)=U_d+α \,t$  on obtient encore ainsi  $U_e=\frac{U_m}{\sqrt{3}}$  si l’appareil filtre la partie alternative avant de la mesurer, mais dans le cas contraire on obtient :
        $\left⟨u\left(t\right)^2 \right⟩= U_d^{\:2} + 2 \:U_d \:α \:\left⟨t\right⟩+α^2 \:\left⟨t^2 \right⟩=U_d^{\:2}+U_e^{\:2}$
c’est-à-dire que la valeur efficace est :  $U_{eff}=\sqrt{U_d^{\:2}+U_e^{\:2}}$  supérieure à $U_d$ et à $U_e$ mais inférieure à  $U_d+U_e$ .

• Expérimentalement, on étudie d’abord des signaux sinusoïdaux de fréquence  $50,0±0,4 \:\mathrm{Hz}$  pour lesquels sont prévus les multimètres.

On ajoute une tension de décalage $U_d$ au signal, puis on mesure $U_{m1}$ sur l’écran de l’oscilloscope et $U_{m2}$ avec le multimètre intégré à l’oscilloscope.

$U_d \:\left⟦\mathrm{V}\right⟧$	$U_{m1} \:\left⟦\mathrm{V}\right⟧$	$U_{m2} \:\left⟦\mathrm{V}\right⟧$	$\frac{U_m}{\sqrt{2}} \:\left⟦\mathrm{V}\right⟧$	$U_{eff1} \:\left⟦\mathrm{V}\right⟧$	$U_{eff2} \:\left⟦\mathrm{V}\right⟧$	$\sqrt{U_d^{\:2}+U_e^{\:2} } \:\:\left⟦\mathrm{V}\right⟧$
$0,02 ± 0,02$	$1,00 ± 0,04$	$1,03 ± 0,03$	$0,721 ± 0,022$	$0,711 ± 0,004$	$0,740 ± 0,044$	$0,721 ± 0,023$
$0,50 ± 0,04$	$1,00 ± 0,04$	$1,03 ± 0,03$	$0,721 ± 0,022$	$0,709 ± 0,004$	$0,800 ± 0,044$	$0,877 ± 0,041$
$-1,00 ± 0,07$	$1,00 ± 0,04$	$1,03 ± 0,03$	$0,721 ± 0,022$	$0,709 ± 0,004$	$1,360 ± 0,047$	$1,233 ± 0,070$
$-1,00 ± 0,07$	$3,00 ± 0,11$	$3,06 ± 0,07$	$2,150 ± 0,049$	$2,108 ± 0,013$	$2,440 ± 0,092$	$2,371 ± 0,074$

On compare ensuite $\frac{U_m}{\sqrt{2}}$ et les valeurs efficaces $U_{eff}$ indiquées par deux multimètres en mode alternatif (la deuxième avec celui intégré à l’oscilloscope).

On constate que le multimètre de précision n’est pratiquement pas influencé par le décalage (les écarts sont inférieurs aux incertitudes de mesure), c’est-à-dire qu’il mesure en fait la valeur efficace de la partie alternative du signal (il filtre la partie alternative avant de la mesurer).

Au contraire, le multimètre intégré à l’oscilloscope semble mesurer la valeur efficace “vraie” du signal total, c’est-à-dire :  $U_{eff}=\sqrt{U_d^{\:2}+U_e^{\:2}}$ ,  mais la précision est assez médiocre (le circuit électronique effectue probablement une intégration, assez sensible aux parasites).

• On étudie ensuite de même des signaux triangulaires.

$U_d \:\left⟦\mathrm{V}\right⟧$	$U_{m1} \:\left⟦\mathrm{V}\right⟧$	$U_{m2} \:\left⟦\mathrm{V}\right⟧$	$\frac{U_m}{\sqrt{3}} \:\left⟦\mathrm{V}\right⟧$	$U_{eff1} \:\left⟦\mathrm{V}\right⟧$	$U_{eff2} \:\left⟦\mathrm{V}\right⟧$	$\sqrt{U_d^{\:2}+U_e^{\:2} } \:\:\left⟦\mathrm{V}\right⟧$
$-0,02 ± 0,02$	$1,00 ± 0,04$	$1,04 ± 0,03$	$0,595 ± 0,017$	$0,581 ± 0,003$	$0,620 ± 0,043$	$0,595 ± 0,018$
$-1,00 ± 0,07$	$1,00 ± 0,04$	$1,03 ± 0,03$	$0,589 ± 0,017$	$0,579 ± 0,003$	$1,300 ± 0,047$	$1,161 ± 0,069$
$-1,00 ± 0,07$	$3,00 ± 0,11$	$3,04 ± 0,07$	$1,749 ± 0,041$	$1,720 ± 0,009$	$2,120 ± 0,091$	$2,015 ± 0,069$

On compare alors $\frac{U_m}{\sqrt{3}}$ et les valeurs efficaces $U_{eff}$ indiquées par deux multimètres en mode alternatif (la deuxième avec celui intégré à l’oscilloscope).

On constate que le multimètre de précision n’est pratiquement pas influencé par le décalage, c’est-à-dire qu’il mesure la valeur efficace de la partie alternative du signal.

Au contraire, le multimètre intégré à l’oscilloscope semble mesurer la valeur efficace “vraie” du signal total,  mais la précision est assez médiocre.

• Si enfin on ajoute un décalage très grand, à tel point d’aboutir à une déformation du signal par saturation aux environs de $±15 \:\mathrm{V}$ (saturation des A.O. des dispositifs électroniques), alors on constate que les mesures semblent devenir incohérentes. Cela est dû au fait que la valeur efficace dépend de la forme du signal (par exemple, coefficients $\sqrt{2}$ et $\sqrt{3}$ différents selon que le signal est sinusoïdal ou triangulaire).

Ainsi, même si on n’a besoin que de mesurer les valeurs efficaces, il est prudent de toujours contrôler la forme des signaux à l’oscilloscope pour s’assurer que ce qui s’affiche sur le multimètre correspond bien à ce qu’on veut mesurer (il faut ne JAMAIS faire confiance aveuglément aux appareils de mesure).

1.3. Mode alternatif ; influence de la fréquence

• En principe, la mesure de la valeur efficace ne dépend pas de la fréquence du signal. Mais pour les générateur qui mesurent la valeur efficace de la partie alternative, le dispositif de filtrage avant mesure ne fonctionne pas aussi bien à toutes les fréquences (les très basses fréquences sont très semblables au continu).

• On étudie d’abord des signaux sinusoïdaux (la tension de décalage $≈ 30 \:\mathrm{mV}$ est négligeable) :

$f \:\:\left⟦\mathrm{Hz}\right⟧$	$U_{m1} \:\left⟦\mathrm{V}\right⟧$	$U_{m2} \:\left⟦\mathrm{V}\right⟧$	$\frac{U_m}{\sqrt{3}} \:\left⟦\mathrm{V}\right⟧$	$U_{eff1} \:\left⟦\mathrm{V}\right⟧$	$U_{eff2} \:\left⟦\mathrm{V}\right⟧$
$5,00±0,04$	$3,00±0,15$	$3,06±0,07$	$1,755±0,041$	$1,58±0,03$	$1,760±0,089$
$50,0±0,3$	$3,00±0,11$	$3,06±0,07$	$1,755±0,041$	$1,728±0,009$	$1,800±0,089$
$500±5$	$3,00±0,11$	$3,06±0,07$	$1,755±0,041$	$1,733±0,009$	$1,800±0,089$
$\left(50,0±0,3\right).{10}^3$	$3,00±0,11$	$3,04±0,07$	$1,749±0,041$	$1,710±0,009$	$1,760±0,089$

On constate ici encore que le multimètre intégré à l’oscilloscope n’est pas influencé par le changement de fréquence. Au contraire, le multimètre de précision, qui mesure la valeur efficace de la partie alternative, affiche un résultat très approximatif (et très fluctuant) à trop basse fréquence.

1.4. Mode continu

• À haute fréquence (petite période), un multimètre en mode continu mesure la moyenne du signal sur un grand nombre de périodes. Pour un signal de la forme :  $u\left(t\right)=U_d+U_m \:\sin⁡\left(ω \,t\right)$  on obtient :  $\left⟨u\left(t\right)\right⟩=U_d$  (et de même pour un signal triangulaire décalé).

À basse fréquence (grande période), un multimètre en mode continu mesure sur une durée très inférieure à la période ; il suit ainsi l’évolution de $u\left(t\right)$.

Aux fréquences intermédiaires, de l’ordre du hertz, le multimètre essaye de suivre $u\left(t\right)$ mais mesure en fait une moyenne sur une durée plus ou moins inférieure à la période : l’affichage fluctue sans cesse de façon apparemment chaotique.

2. Utilisation en “fréquencemètre” ; effets “stroboscopiques”

• Peut-être un jour, si des étudiants fournissent des données...

3. Décomposition en série de Fourier

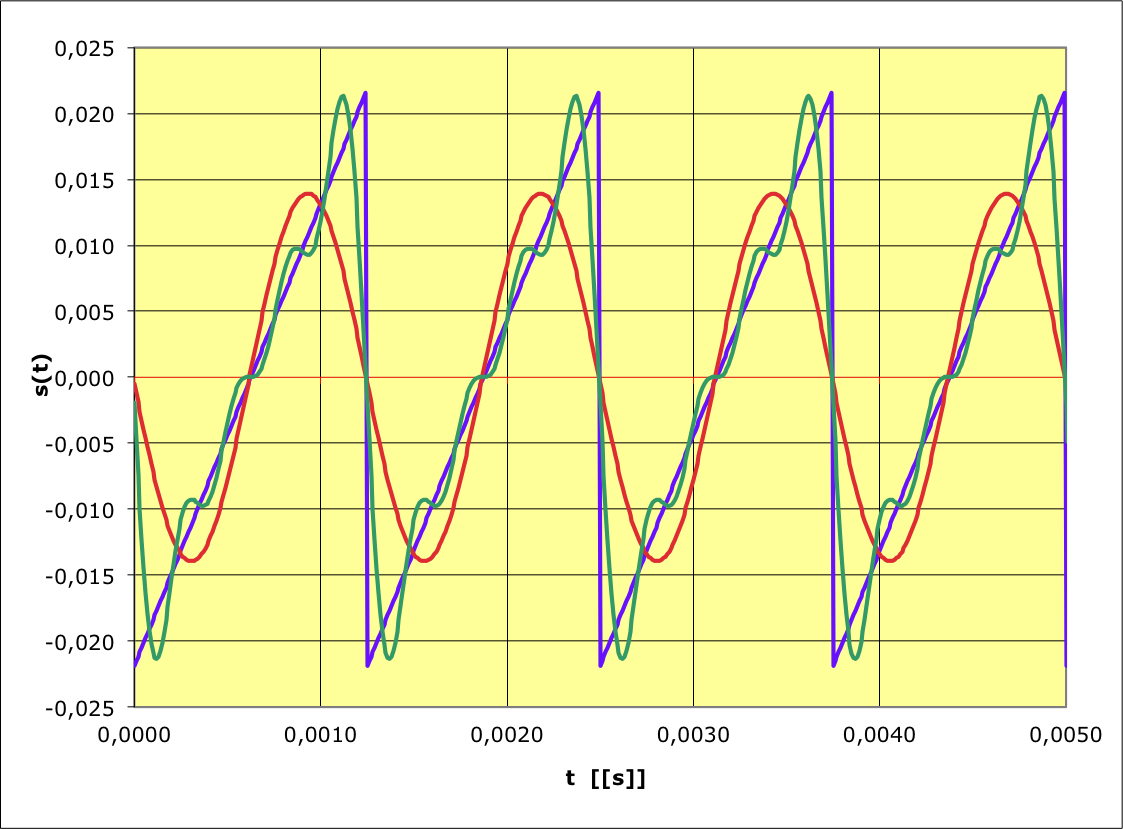
◊ remarque : ne disposant pas de données expérimentales, on choisit ici de se baser sur un signal simulé, partant du principe que la méthode peut être étudiée aussi efficacement ainsi ; on choisit un signal en “dents de scie” car il présente une nette discontinuité qui pourrait sembler difficile à reproduire à l'aide des courbes régulières que sont les sinusoïdes.

• Avec un tableur, assisté d'un solveur, on ajuste jusqu'à l'ordre 4 une somme de Fourier pour approcher un signal en “dents de scie”. La comparaison de simulations successives aux ordres intermédiaires (ici 1 et 4) donne une idée de l'efficacité de la méthode.

 

◊ remarque : sur cet exemple on a utilisé Excel avec le solveur associé de Frontline systems (c'est nettement plus rapide que de chercher par tâtonnements) ; c'est aussi possible avec LibreOffice (le solveur de la version 6 en mode non linéaire y parvient avec un peu d'aide), ou en utilisant le solveur minimi (dans un tableur, Maple ou python).

• Le résultat obtenu n'est pas exactement le même en ajustant successivement chaque terme ou en ajustant globalement. Par exemple, l'ajustement individuel du terme fondamental donne :  $S_{1m}=0,013936$  et  $φ_1=1,607 \:\mathrm{rad}$  ;  la contribution du fondamental dans l'ajustement global d'ordre 4 donne  :  $S_{1m}=0,013934$  et  $φ_1=1,605 \:\mathrm{rad}$ .  De façon générale la différence semble ici négligeable (nettement inférieure aux incertitudes de mesure usuelles) mais cela peut dépendre de la forme du signal étudié.