• Les “ondes” (ondes progressives) sont des signaux qui se
déplacent dans l'espace en fonction du temps (sans déplacement
global de matière).
Dans les milieux non dispersifs, toutes les composantes de
Fourier se déplacent à la même vitesse, donc de même pour un
signal quelconque, dont la forme reste inchangée lors de la
propagation.
◊ remarque : sur les plages, la propagation des vagues est
dispersive ; les ondes de plus haute fréquence se déplacent plus
vite, c'est ce qui cause le déferlement des vagues (le sommet
avance plus vite que la base).
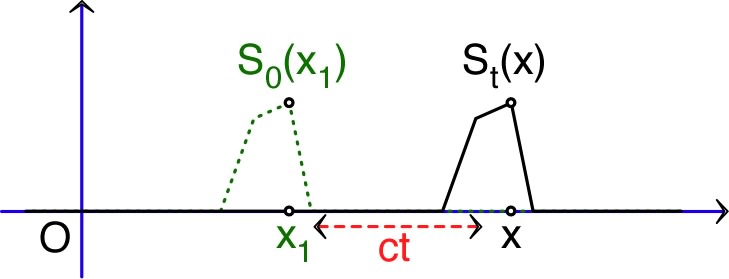
• Considérons un signal dépendant de la position (une seule
coordonnée) et qui, à l'instant initial, peut s'écrire sous la
forme
. Supposons que le signal se propage sans déformation ni
amortissement.

Soit la
“célérité” (vitesse de propagation) d'un signal, alors à un
instant
on doit retrouver en
la même valeur du signal initial en
:
.
La mesure du retard dû à la propagation d'un signal donne la
célérité :
;
.
◊ remarque : si le signal se propage à la célérité mais dans
l'autre sens (célérité algébrique
) on
obtient de même :
.
• On peut inversement s'intéresser à l'évolution dans le temps
pour une abscisse fixée :
.
• Pour un signal sinusoïdal, on peut par exemple écrire, avec
une période
, une
longueur d'onde (“période spatiale”)
et où la constante (déphasage)
dépend du choix des origines pour et :
| . |
◊ remarque : la pulsation est
(avec la fréquence
) ; on peut aussi définir un “vecteur d'onde”
orienté comme la propagation et tel que
.
• Le “pincement” d'une corde de guitare (ou de Melde) cause la
propagation de deux signaux progressifs dans les deux sens. Aux
extrémités, l'énergie des signaux est peu absorbée : ils sont
réfléchis car le support s'oppose au mouvement et cette réaction
crée une onde opposée qui se propage dans l'autre sens. L'effet
résultant est une superposition “continuelle” de signaux se
propageant dans les deux sens.
• D'après le principe de décomposition de Fourier, on peut
étudier la réflexion à l'origine en considérant la superposition
de deux signaux sinusoïdaux de même amplitude :
| ; | |
| . |
On obtient bien ainsi l'immobilité de la corde
pour ,
mais au voisinage le signal résultant semble “osciller sur place”
en fonction de
, avec une
amplitude qui dépend de (les
dépendances en et sont
séparées). On nomme cela “ondes stationnaires” (sans propagation
apparente).
Les positions où l'onde stationnaire est nulle sont appelées
“nœuds” ; celles où l'amplitude est maximale sont nommées
“ventres” d'oscillation. L'écart entre deux nœuds, ou entre deux
ventres, est multiple de
.
• Le même phénomène se produit de même à l'autre extrémité ; en
notant
et
on peut écrire :
| ; | |
| . |
L'immobilité de la corde
est bien obtenue pour ,
mais cela n'est compatible avec le comportement en que
si les nœuds et les ventres se correspondent :
, c'est à dire
(avec
).
• Pour les longueurs d'onde ne respectant pas cette condition,
les réflexions successives aux extrémités donnent rapidement une
superposition “aléatoire” qui disparaît par compensation de termes
de signes contraires, d'autant plus qu'il y a ensuite
amortissement.
Pour les “fréquences de résonance” de la corde (vérifiant la
condition précédente) on obtient au total une oscillation
“stationnaire”, restant visible bien que finissant par être
amortie, avec une amplitude dépendant
du lieu, ce qui peut se réécrire sous la forme :
; .
◊ remarque : cette propriété est très générale ; la propagation
d'ondes dans un milieu limité ne peut se faire significativement
que pour un ensemble de fréquences de résonance caractéristiques
du milieu.
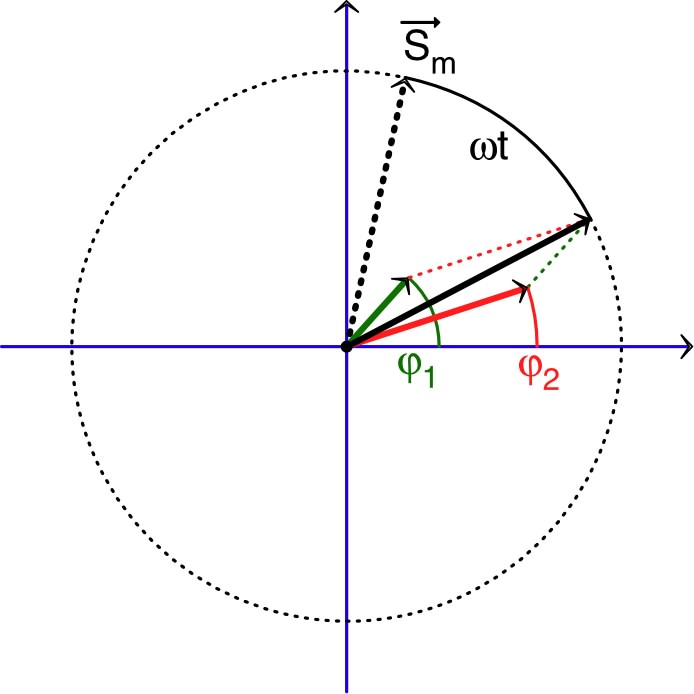
• Pour ceux qui préfèrent une représentation graphique plutôt que
des expressions algébriques, les diagrammes de Fresnel permettent
de visualiser graphiquement la superposition de deux signaux à
l'aide de vecteurs tournants : le signal algébrique correspond à
la projection sur l'axe horizontal.
Pour des signaux se propageant dans le même sens, on peut
utiliser des vecteurs tournant dans le sens trigonométrique à la
vitesse angulaire
, avec une
position initiale correspondant à la phase
.
◊ remarque : une représentation par des nombres complexes est
possible.
 |
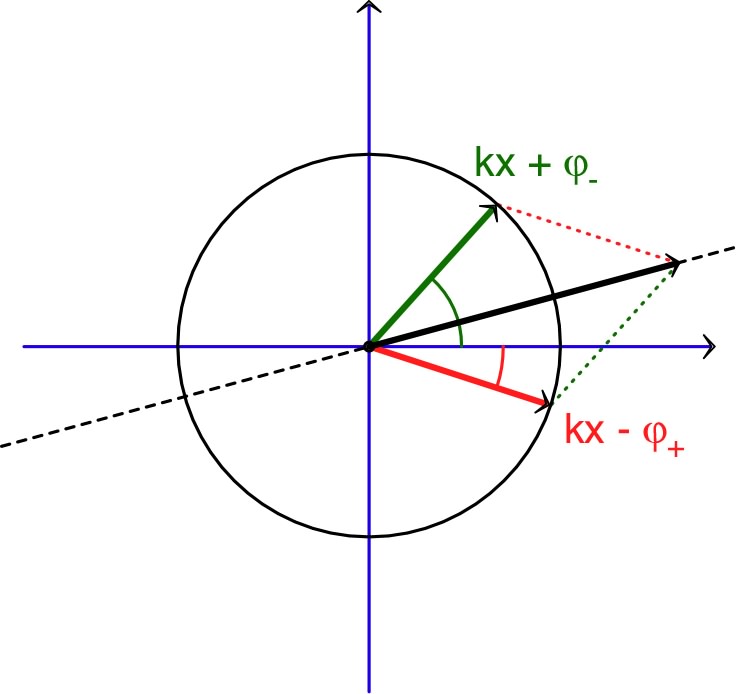 |
Pour une propagation en sens contraire, compte tenu de la parité
du cosinus, on peut utiliser des vecteurs tournant dans le sens
horaire. En particulier pour deux signaux de même amplitude, on
peut aussi justifier graphiquement l'oscillation stationnaire.
📖 exercices n° I et II.
• Ce phénomène se généralise à plusieurs dimensions, par exemple
pour l'interférence des ondes à la surface de l'eau.

Selon le retard dû à la propagation, la superposition peut être constructive ou destructive.
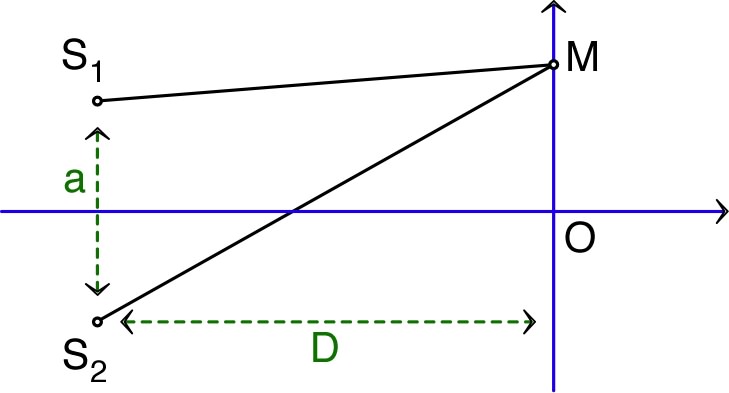
| ◊ lorsque la différence de chemin parcouru par les deux parties de l'onde (“différence de marche”) est multiple de la longueur d'onde, leurs effets s'ajoutent (interfèrent) constructivement ; | |
| ◊ si la différence de marche est décalée d'une demi longueur d'onde, l'interférence est destructive (absence d'oscillation) ; | |
| ◊ en notant l'écart algébrique d'un point de l'écran par rapport à l'origine sur l'axe, la différence de marche peut s'écrire : ; | |
| ◊ en simplifiant au premier ordre d'approximation ( et ) : ; | |
| ◊ l'interférence constructive pour où correspond à des franges d'interférence séparées par l'interfrange : . |
◊ remarque : cela correspond à des directions telles
que
.
◊ remarque : l'interférence est d'autant moins marquée loin de l'axe de symétrie, car les ondes y ont des amplitudes différentes (indépendamment de l'amortissement, l'énergie des ondes circulaires “s'étale” en se propageant, donc leur amplitude diminue en conséquence).
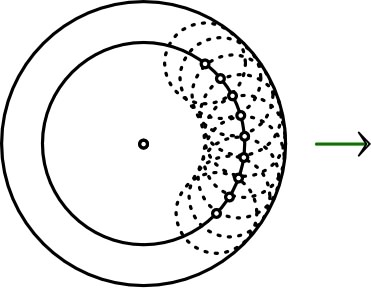
• Le principe des ondelettes d'Huygens - Fresnel suppose que
chaque point du front d'onde réémet une ondelette sphérique. Il
suffit d'en représenter quelques unes pour visualiser la surface
enveloppe des ondelettes, seul lieu où elles interfèrent
constructivement, décrivant le front d'onde suivant.
 |
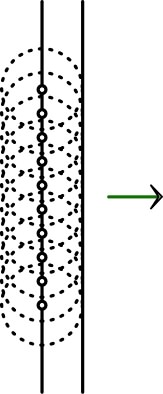 |
On constate ainsi que, dans un milieu homogène et isotrope, une
onde plane, cylindrique ou sphérique continue à se propager de la
même façon.
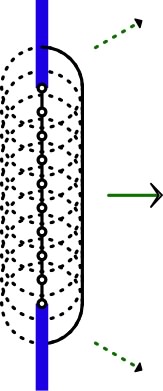
• Lorsqu'une onde plane est limitée par les bords d'un obstacle,
les ondelettes des bords suggèrent qu'une partie de l'énergie de
l'onde est “diffractée”.
Pour un faisceau large, cette diffraction est négligeable en
proportion de l'énergie totale de l'onde : on considère que le
faisceau est “limité” par les bords mais que la propagation de la
partie qui continue n'est pas modifiée.
 |
 |
Par contre, si on essaie de limiter fortement un faisceau
(largeur
“comparable” à la longueur d'onde), la diffraction peut être
importante en proportion : une partie non négligeable de l'énergie
est diffractée dans un angle tel que
.
📖 exercice n° III.