PROPAGATION DES SIGNAUX - corrigé des exercices

I. Propagation et réflexions

1.a.	• Pour se propager jusqu'en  $x_1$ ,  le signal met une durée  $t_1=\frac{x_1}{c}=200 \:\mathrm{ms}$ . • La représentation de $s_0 \left(t\right)$ et  $s_1 \left(t\right)=s_0 \left(t-t_1 \right)$  a donc l'allure ci-dessous.
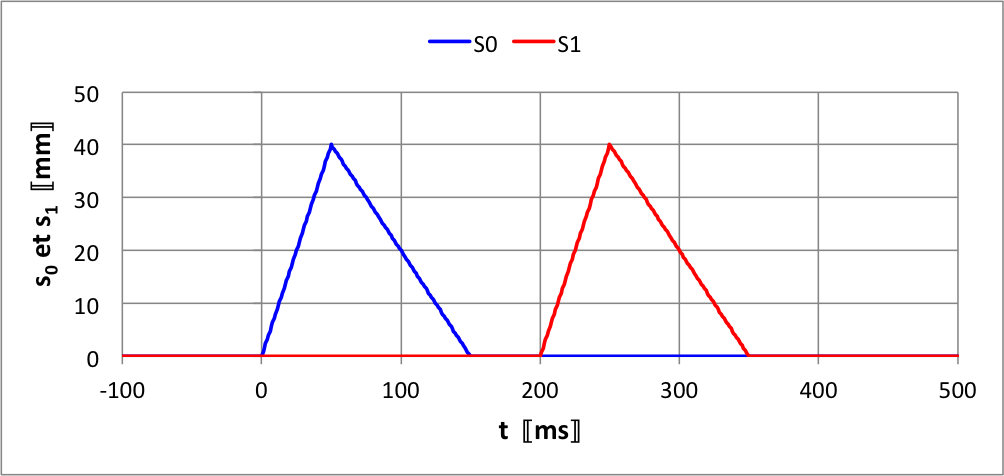
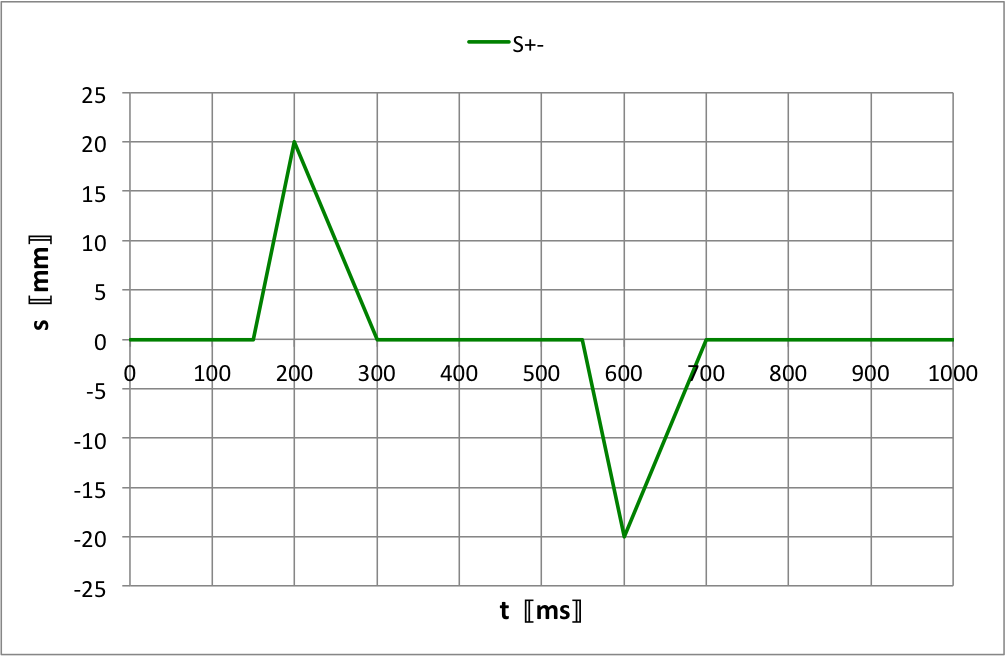
1.b.	• Il faut prendre la précaution de tenir compte d'une éventuelle réflexion si le signal se propage jusqu'à l'extrémité de la corde : la durée nécessaire est  $T=\frac{L}{c} =500 \:\mathrm{ms}$  (il est totalement réfléchi après  $650 \:\mathrm{ms}$). Le premier exemple est donc avant réflexion. • Puisque le signal est simple, on peut se contenter de déterminer la position de trois points caractéristiques :  le début est en  $x_d=c \:t$  ;  le sommet est en  $x_s=c .\left(t-τ\right)$  ;  la fin est en  $x_f=c .\left(t-3τ\right)$ . ◊ remarque : la partie au début du signal est plus à droite (plus avancée), alors qu'en fonction du temps elle est plus à gauche (plus tôt). • Pour formaliser plus systématiquement, si on note  $s_0 \left(t\right)=f\left(t\right)$  alors  $s_x \left(t\right)=f\left(t-\frac{x}{c}\right)$ .  Ceci correspond aussi à  $s_t \left(x\right)=f\left(t-\frac{x}{c}\right)$  en raisonnant en fonction de $x$ a un instant donné (sans réflexion) ; on peut par ailleurs préférer exprimer à l'aide de  $x-c \:t$  (ici pour $t_2$) : ◊ pour  $t-\frac{x}{c}<0$ :   $c \:t<x$  ;  $s_t \left(x\right)=0$  ; ◊ pour  $0≤t-\frac{x}{c}≤τ$ :   $c .\left(t-τ\right)≤x≤c \:t$  ;  $s_t \left(x\right)=-2 \frac{α}{c} \left(x-c \:t\right)$  ; ◊ pour  $τ≤t-\frac{x}{c}≤3τ$ :   $c .\left(t-3τ\right)≤x≤c .\left(t-τ\right)$  ;  $s_t \left(x\right)=\frac{α}{c} \left(3c \:τ+x-c \:t\right)$  ; ◊ pour  $3τ≤t-\frac{x}{c}$ :  $x≤c .\left(t-3τ\right)$  ;  $s_t \left(x\right)=0$. 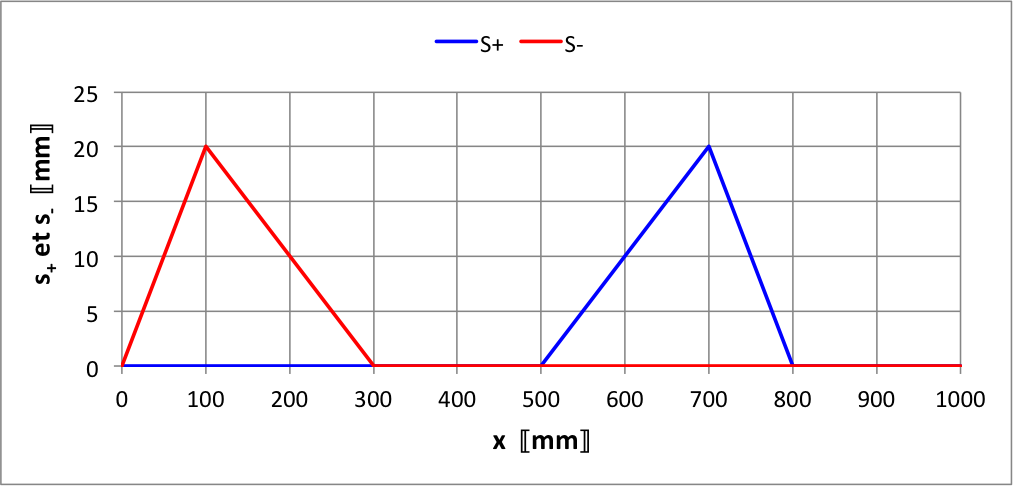• Lors de la réflexion, le support exerce sur la corde les forces nécessaires pour l'empêcher de bouger, donc cela crée un signal réfléchi de signe contraire, se propageant en sens inverse. • Pour le calculer, on change le signe et on peut utiliser les expressions précédentes pour  $t_3$ ,  en remplaçant la variable $x$ (position étudiée) par  $x'=2L-x$  (position à laquelle serait arrivé le signal s'il ne s'était pas réfléchi). 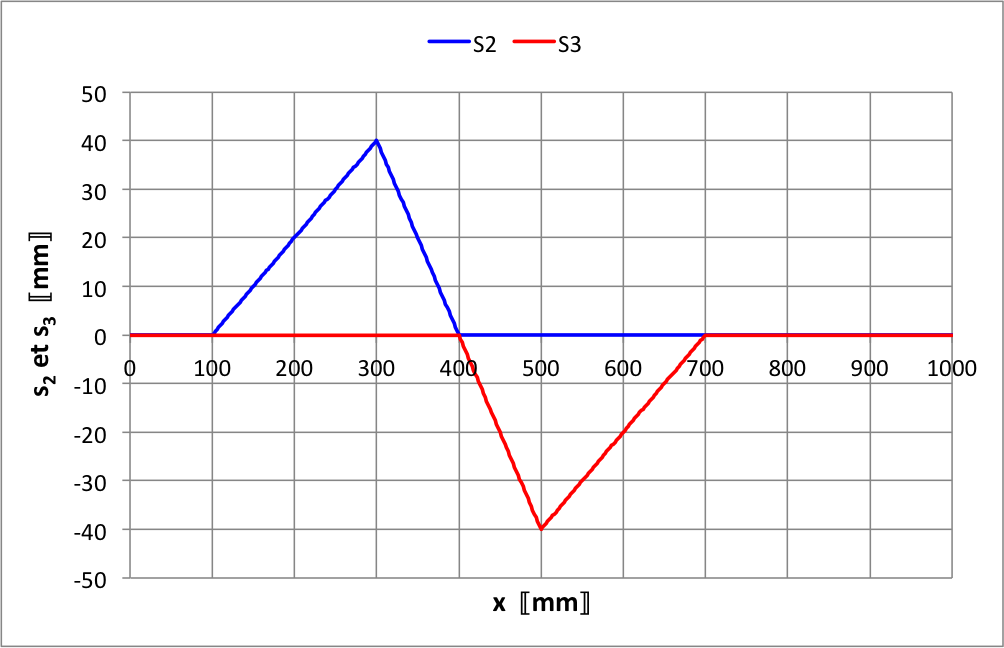• Puisque le signal est simple, on peut se contenter de déterminer la position de trois points caractéristiques :  le début est en  $x_d=2L-c \:t$  ;  le sommet est en  $x_s=2L-c .\left(t-τ\right)$  ;  la fin est en  $x_f=2L-c .\left(t-3τ\right)$. ◊ remarque : la partie au début du signal réfléchi est plus à gauche (plus avancée dans le retour). 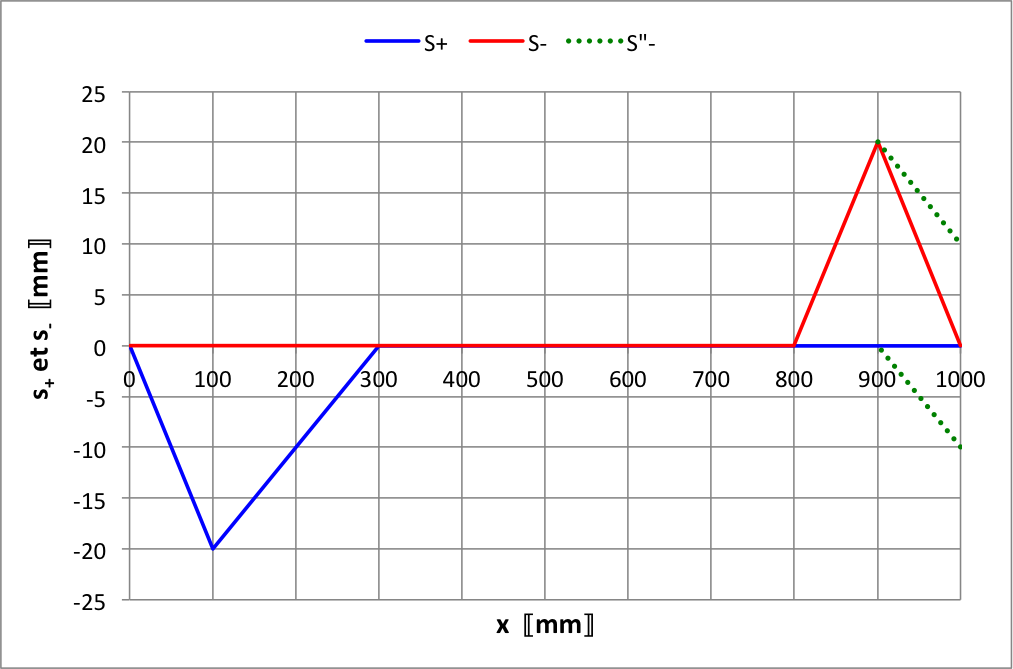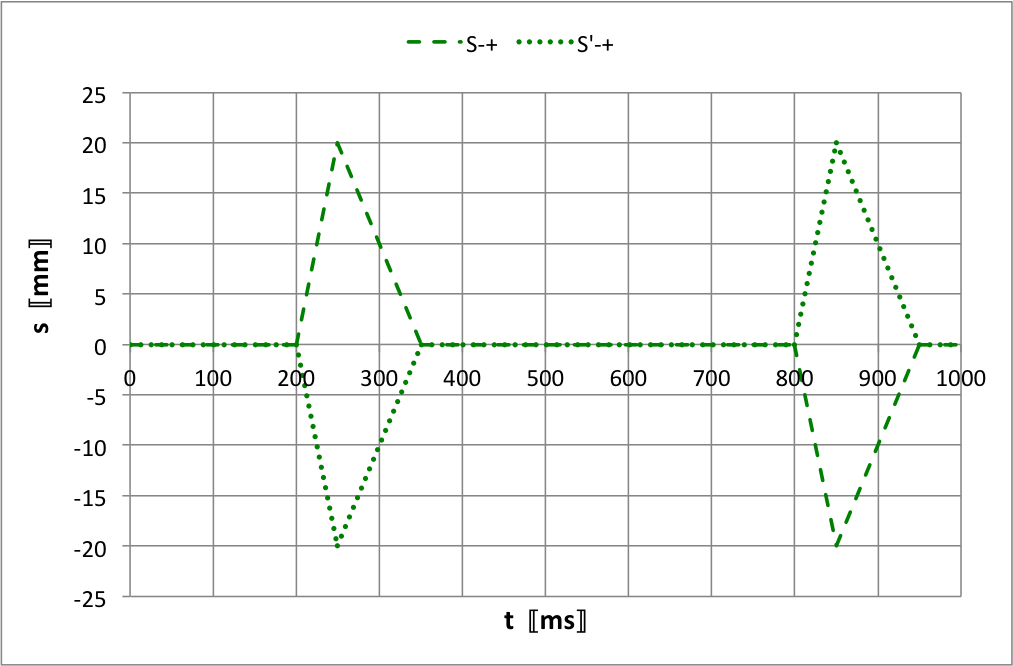• La représentation de $s_2 \left(x\right)$ et $s_3 \left(x\right)$ a ainsi l'allure ci-dessous.

2.a.	• Si on impose le signal en un point de la corde qui n'est pas une extrémité, cela revient à générer deux signaux d'amplitude moitié (de même signe) se propageant dans les deux sens. • À l'instant  $t_2=200 \:\mathrm{ms}$  (la forme des signaux est inchangée) : ◊ l'avant de la partie qui se propage vers  $x=L$  est arrivé en  $x_{2d}=x_1+c \:t_2=80 \:\mathrm{cm}$  ; ◊ l'avant de la partie qui se propage vers  $x=0$  est arrivé en  $x'_{2d}=x_1-c \:t_2=0 \:\mathrm{cm}$. • On constate qu'il n'y a pas de réflexion ni superposition deux parties du signal.
	• À l'instant  $t_3=800 \:\mathrm{ms}$  (la forme des signaux est inchangée) : ◊ l'avant de la partie qui se propage vers  $x=L$  s'y est réfléchi en changeant de signe ; il serait arrivé en  $x_{3d}=x_1+c \:t_3=200 \:\mathrm{cm}$ ,  donc il est revenu en  $x_{3d}=2L-\left(x_1+c \:t_3 \right)=0 \:\mathrm{cm}$  ; ◊ l'avant de la partie qui se propage vers  $x=0$  s'y est réfléchi en changeant de signe ; il serait arrivé en  $x'_{3d}=x_1-c \:t_3=-120 \:\mathrm{cm}$ ,  donc revenu en  $x'_{3d}=-\left(x_1-c \:t_3 \right)=120 \:\mathrm{cm}$  mais s'est réfléchi en  $x=L$  (rechangeant de signe) et est revenu en  $x'_{3d}=2L+\left(x_1-c \:t_3 \right)=80 \:\mathrm{cm}$  ; ◊ mais l'arrière de cette partie est arrivé seulement en  $x'_{3f}=-\left(x_1-c. \left(t_3-3τ\right)\right)=90 \:\mathrm{cm}$  et n'a pas encore fait la seconde réflexion ; entre le sommet de la portion réfléchie et la limite $L$, la superposition avec la partie non réfléchie donne un raccordement affine (signal nul en  $x=L$). • On constate par contre qu'il n'y a pas superposition des deux parties du signal.
2.b.	• En  $x=0$  la corde est bloquée par le support, le signal total est donc toujours nul (représentation graphique inutile) ; il peut toutefois être intéressant d'y étudier le passage avec réflexion du signal afin de montrer comment s'effectue la compensation. • Puisque la corde est de longueur finie et qu'il se produit des réflexions aux extrémités, le fait de négliger tout amortissement conduit à un signal de durée infinie... non représentable graphiquement. On choisit donc ici de se limiter à représenter un intervalle de temps permettant d'observer en  $x=0$  une première réflexion de chacune des deux parties du signal (cela suffit à comprendre le principe du raisonnement) : ◊ l'avant de la partie qui se propage vers  $x=0$  y parvient en  $t_d=\frac{x_1}{c}=200 \:\mathrm{ms}$  ;  l'arrière n'y parvient qu'en  $t_f=t_d+3τ=350 \:\mathrm{ms}$  ; ◊ l'avant de la partie qui se propage vers  $x=L$  s'y réfléchit puis parvient en  $x=0$  (inversé) en  $t'_d=\frac{2L-x_1}{c}=800 \:\mathrm{ms}$  ;  l'arrière n'y parvient qu'en  $t'_f=t'_d+3τ=950 \:\mathrm{ms}$ . ◊ remarque : la première partie serait de retour en  $x=0$  à l'instant  $t''_d=\frac{2L+x_1}{c}=1200 \:\mathrm{ms}$  (et ainsi de suite...).
	• Puisque la corde est de longueur finie et qu'il se produit des réflexions aux extrémités, le fait de négliger tout amortissement conduit à un signal de durée infinie... non représentable graphiquement. On choisit donc ici de se limiter à représenter un intervalle de temps permettant d'observer en  $x_4=70 \:\mathrm{cm}$  une première passage de chacune des deux parties du signal (cela suffit à comprendre le principe du raisonnement) : ◊ l'avant de la partie qui se propage vers  $x=L$  parvient en $x_4$ à  $t'_{4d}=\frac{x_4-x_1}{c}=150 \:\mathrm{ms}$  ;  l'arrière n'y parvient qu'à  $t'_{4f}=t'_{4d}+3τ=300 \:\mathrm{ms}$  ; ◊ l'avant de la partie qui se propage vers  $x=0$  s'y réfléchit puis parvient en  $x_4$  (inversé) en  $t_{4d}=\frac{x_1+x_4}{c}=550 \:\mathrm{ms}$  ;  l'arrière n'y parvient qu'en  $t_{4f}=t_{4d}+3τ=700 \:\mathrm{ms}$ . ◊ remarque : on constate qu'il n'y a pas superposition des deux parties du signal, car la première partie serait ne serait de retour en  $x_4$  qu'à l'instant  $t'_{4d}=\frac{2L+x_4-x_1}{c}=1150 \:\mathrm{ms}$  (et ainsi de suite...).

II. Conditions aux limites

III. Diffraction des sons