AM II - DÉRIVÉES ET DIFFÉRENTIELLES

1. Fonctions d'une variable

1.1. Notations des physiciens

• Pour une fonction  $x\overset{f}{⟶}y=f\left(x\right)$ ,  les physiciens raisonnent souvent simplement sur l'expression  $y\left(x\right)$.  L'expression  $f'\left(x\right)$  de la fonction dérivée est alors notée  $y'\left(x\right)=\frac{dy\left(x\right)}{dx}$ .

Cette notation (de Liebniz) vient de :  $f'\left(x\right)=\underset{δx→0}{lim}\frac{δy\left(x\right)}{δx}$   où   $δy\left(x\right)=y\left(x+δx\right)-y\left(x\right)$ .

Les notations “différentielles” $dx$ et $dy$ symbolisent le comportement limite de petites variations $δx$ et $δy$ (infinitésimales).

• Plus précisément, au proximité d'une valeur particulière de $x$ (au point $M$ de la courbe), on peut associer à tout point voisin sur la courbe un point projeté sur la tangente (le résultat ne dépend pas du type de projection utilisé).

Les variations $dy$ et $dx$ vérifient toujours, même si elles ne sont pas petites :  $dy=f'\left(x\right) \; dx$ .

Par contre les approximations  $δx≈dx$  et  $δy≈dy$  ne sont valables que pour $δx$ et $δy$ infinitésimales.

◊ remarque : une ambiguïté apparaît hélas souvent, car la différence entre les notations  $\left(δx,\, δγ\right)$  et  $\left(dx,\, dγ\right)$  est généralement omise.

1.2. Notation mathématiques

• Les notations des mathématiciens sont généralement différentes, car ils privilégient les raisonnement sur les fonctions plutôt que sur les expressions.

Les mathématiques considèrent ainsi que la différentielle $df\left(x\right)$ est une fonction linéaire dans la base locale, dont le graphique correspond à la tangente à la courbe :  $α\overset{\;\;df\left(x\right)\;\;}{\xrightarrow}β=f'\left(x\right).α$ .

Raisonnant de même pour la différentielle dx, considérée comme une fonction “identité” :  $α\overset{dx}{⟶}α$ ,  on aboutit ainsi à  $df\left(x\right)=f'\left(x\right) \; dx$ ,  mais considérée ici comme une relation linéaire entre fonctions.

◊ remarque : avec ces notations, les quantités $α$ et $β$ correspondent aux quantités que le physicien note $dx$ et $dy$.

◊ remarque : ces notations mathématiques ont été introduites car elles ont l'avantage de simplifier certains raisonnements abstraits, mais elles ont l'inconvénient de s'éloigner plus de l'interprétation usuelle en physique (il faut ne pas confondre les quantités physiques et les modèles mathématiques utilisés pour les représenter).

2. Fonctions de plusieurs variables

2.1. Notations des physiciens

• Pour une fonction de deux variables  $\left(x, y\right)\overset{f}{⟶}z=f\left(x,y\right)$ ,  dont le graphique serait une surface dans l'espace à trois dimensions, le physicien raisonne avec l'expression  $z\left(x, y\right)$.

On peut dériver “partiellement” par rapport à l’une des variables en considérant (pour cette dérivation) l'autre variable comme constante ; ainsi :  ${f}_{x}'\left(x, y\right)=\underset{\underset{y=Cte}{δx→0}}{lim}\frac{z\left(x+δx, y\right)-z\left(x, y\right)}{δx}$   et de même pour  ${f}_{y}'\left(x, y\right)$.

Dans le cas général, la variation $δz$ est due à la somme des effets causés par $δx$ et par $δy$ ; le comportement limite des petites variations doit donc être décrit par une “différentielle” de la forme :  $dz={f}_{x}'\left(x, y\right)\; dx+{f}_{y}'\left(x, y\right)\; dy$ .

Ici  ${f}_{x}'\left(x, y\right)≠\frac{dz}{dx}$  ;  par analogie avec les notations pour les fonctions d'une seule variable, les physiciens écrivent généralement :  $\frac{∂f\left(x, y\right)}{∂x}$  ou   ${\left[\frac{∂f}{∂x}\right]}_{y}$ .

• Soit par exemple un point $M$ $\left[x, y\right]$ dans un plan ; on étudie la surface délimitée par les axes et le point $M$ :  $S=S\left(x, y\right)=x \: y$ .

Dans ce cas :  ${\left[\frac{∂S}{∂x}\right]}_{y}=y$   ;   ${\left[\frac{∂S}{∂y}\right]}_{x}=x$ .

• Ainsi, au voisinage d'un point $\left[x, y\right]$ particulier, on peut exprimer les “petites” variations  $dS$  de la surface à partir des “petites” variations  $dx$  et  $dy$  des variables :  $dS={\left[\frac{∂S}{∂x}\right]}_{y}\, dx+{\left[\frac{∂S}{∂y}\right]}_{x}\, dy=y\;dx+x\;dy$ .

2.2. Notations mathématiques

• De façon analogue, les mathématiques peuvent décrire une fonction :  $\left(x, y\right)\overset{f}{⟶}z=f\left(x,y\right)$ .

La différentielle  $df\left(x, y\right)$  est alors définie comme fonction linéaire dans la base locale, dont le graphique correspond au plan tangent à la surface :  $\left(α, β\right)\overset{\;\;df\left(x, y\right)\;\;}{\xrightarrow}γ={f}_{x}'\left(x, y\right).α+{f}_{y}'\left(x, y\right).β$ .

Raisonnant de même pour les différentielles $dx$ et $dy$, considérées comme des fonctions “projection” :  $\left(α, β\right)\overset{dx}{⟶}α$   et   $\left(α, β\right)\overset{dy}{⟶}β$ ,  on aboutit ainsi à  $df\left(x, y\right)={f}_{x}'\left(x, y\right)\; dx+{f}_{y}'\left(x, y\right)\; dy$ ,  mais considérée ici comme une relation linéaire entre fonctions.

3. Variables non indépendantes

• Dans certains cas, on utilise des expression dans lesquelles interviennent plusieurs grandeurs physiques non indépendantes.

Pour un point $M$ $\left[x, y\right]$ dans un plan, on peut être amené à considérer le cas où $M$ est contraint à se déplacer sur une droite d’équation   $y=y\left(x\right)=a \;x+b$ .

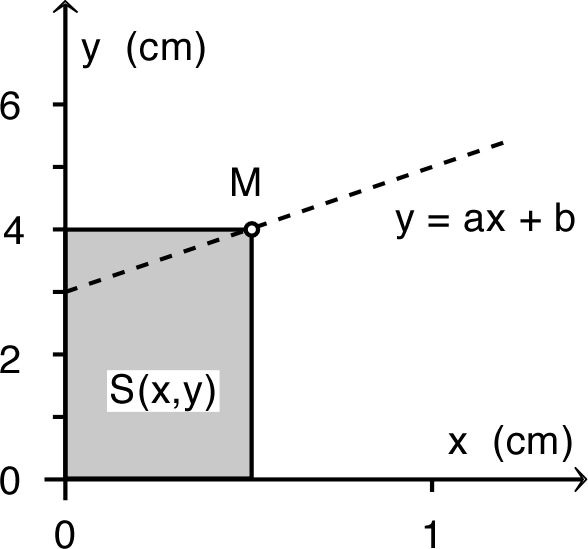
Ainsi, si on raisonne en fonction de $x$, on est amené à considérer $S$ comme :  $S\left(x\right)=S\left(x, y\left(x\right)\right)=x.\left(a \:x+b\right)$  ;  on peut alors décomposer les variations de $S$ en deux effets :
    ◊ celui causé directement par la variation $dx$ ;
    ◊ celui découlant de la variation $dy$ provoquée par la  variation $dx$.

On obtient alors par l'intermédiaire de la fonction de deux variables :
    $dS={\left[\frac{∂S}{∂x}\right]}_{y}\, dx+{\left[\frac{∂S}{∂y}\right]}_{x}\, dy=y\;dx+x\;dy$  ;
    $\frac{dS\left(x, y\left(x\right)\right)}{dx}={\left[\frac{∂S}{∂x}\right]}_{y} +{\left[\frac{∂S}{∂y}\right]}_{x} \frac{dy\left(x\right)}{dx}=2 \:a \:x+b$  (dérivée “totale”)  ;
résultat identique à celui obtenu en considérant $S\left(x\right)$ comme fonction d'une variable :  $\frac{dS\left(x\right)}{dx}=2 \:a \:x+b$ .

 exercices n° I et II.

4. Équations différentielles

• Dans, l'exemple précédent, on peut inversement chercher quelle relation  $y=y\left(x\right)$  on doit imposer pour obtenir  $S\left(x\right)=Cte$  indépendante de $x$.

Dans ce cas simple, il est clair que  $S\left(x\right)=x \:y=Cte$  impose  $y\left(x\right)=\frac{Cte}{x}$ .  Mais on peut aussi caractériser la propriété considérée (variation nulle) par l'équation différentielle :  $dS=y\;dx+x\;dy=0$ .

• Si on met l'équation sous la forme :  $\frac{dy\left(x\right)}{dx}=-\frac{y\left(x\right)}{x}$ ,  alors on peut chercher la solution comme fonction “puissance” (d'après  $\frac{∂\left({x}^{n}\right)}{∂x}=n \:{x}^{n-1}=n\frac{{x}^{n}}{x}$).

Ceci donne  $n={-1}$  et, puisque l'équation différentielle est linéaire, toutes les variations de la forme  $y\left(x\right)=\frac{Cte}{x}$  sont solution.

◊ remarque : ce n'est pas la seule façon de résoudre cette équation.