DÉRIVÉES ET DIFFÉRENTIELLES - corrigé des exercices
A. EXERCICES DE BASE
I. Fonction de deux variables
1. • La fonction est définie pour
:
et
; c’est-à-dire :
et
.
2. • En considérant
constant, on obtient :
.
• En considérant
constant, on obtient :
.
• Pour
et
, on
obtient en particulier :
;
;
.
II. Dérivées partielles et dérivée totale
• Les dérivées partielles sont
respectivement :
et
.
• On peut écrire :
puis :
.
• Compte tenu des dérivées partielles
calculées précédemment, la dérivée “totale” a donc effectivement
l’expression indiquée.
B. EXERCICE D'APPROFONDISSEMENT
III. Dérivées partielles et dérivée totale
1. • La fonction est définie pour
.
• La relation
correspond à
(zone hachurée) :
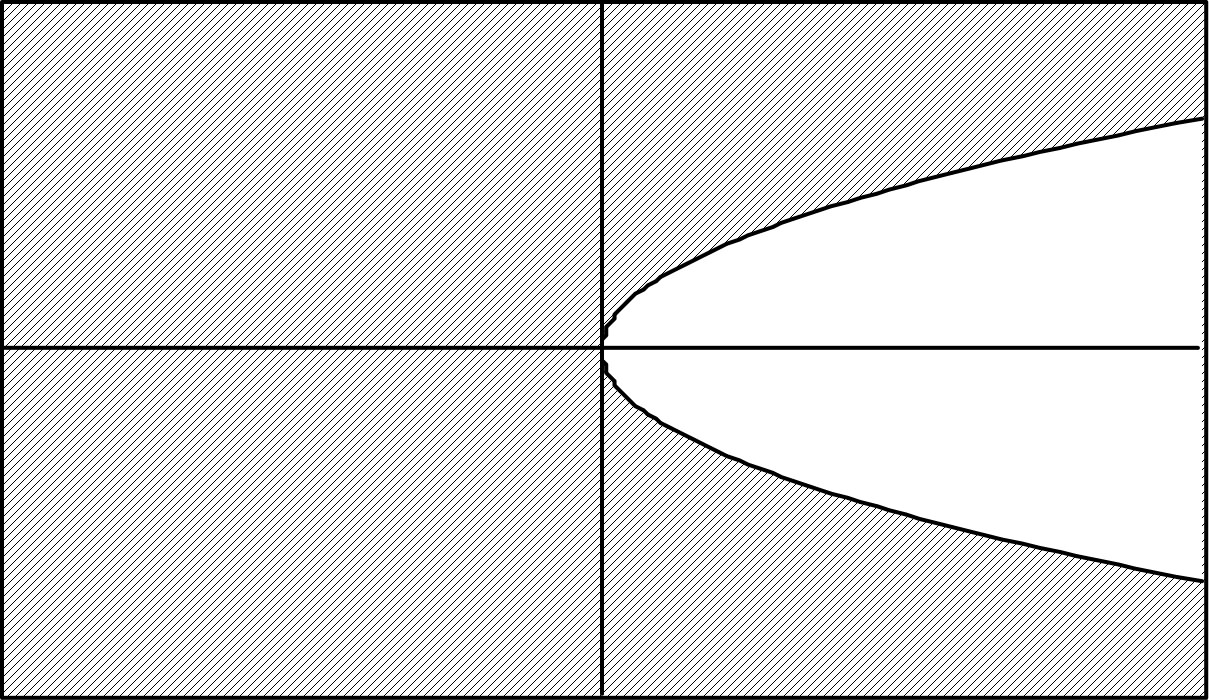
◊ remarque : il est plus rapide
d’étudier
...
• La relation
correspond aux quarts de plan : (
et
)
ou (
et
).
• Le domaine de définition cherché
correspond à : (
et
)
ou (
et
)
; donc par combinaison des deux conditions (zone hachurée) :
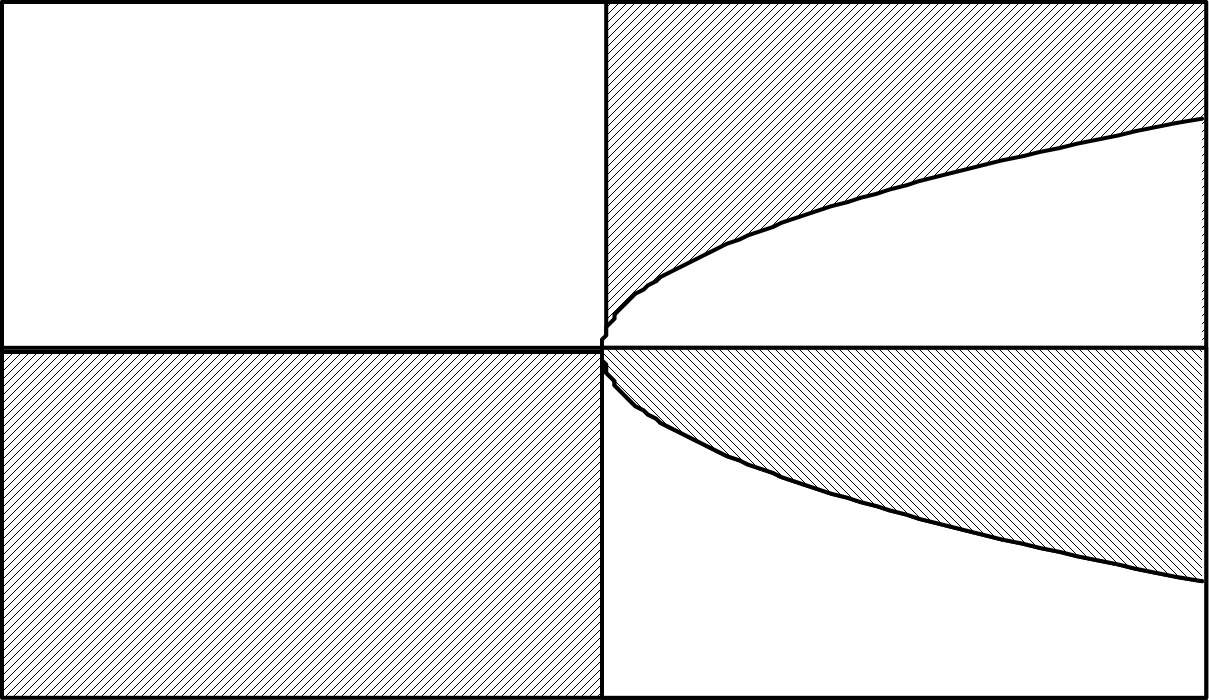
◊ remarque : les limites sont acceptées.
2. • On obtient :
;
.
• Pour :
et
:
;
; .
3. • En substituant
,
on obtient (il y a d’autres formulations possibles) :
;
;
.
◊ remarque : l’équation correspond à
une courbe au moins partiellement dans le domaine de définition de
la fonction (la partie pour et
celle pour
).
• La dérivée totale peut s’écrire,
après simplification :
.
• Par comparaison, après regroupement
au même dénominateur et simplifications, on peut vérifier qu’on
obtient le même résultat pour :
.


