AM. 1 - NOTATIONS DES GRANDEURS PHYSIQUES

 

 

1. Notations mathématiques et physiques

 

1.1. Grandeurs physiques ; importance des unités

 

• Pour construire des modèles de la “réalité”, le physicien représente les grandeurs physiques par des grandeurs mathématiques.

 

Ainsi, l’intensité d’un courant électrique peut être représentée dans un calcul littéral par la lettre , elle peut être représentée dans un calcul numérique par la valeur    ou par la valeur  .

 

Pour le physicien, ces différentes notations ne sont que des représentations différentes d’une même grandeur physique :  .

 

Bien que  ,  il est sûr que    et    sont deux représentations équivalentes d’une même grandeur physique.

 

• Ceci montre en particulier que l’UNITÉ fait partie de “l’expression numérique” d’une grandeur PHYSIQUE.

 

 

1.2. Notation par des “fonctions” ou des “expressions”

 

• Soit une grandeur  dépendant d’une autre grandeur , on peut noter    la relation formelle (fonction) reliant  (variable) et l'expression de  en fonction de  :  .

 

Par exemple, pour un point  de coordonnées  dans un plan, si  se déplace selon une trajectoire d’équation :  ,  alors dans ce cas    représente symboliquement la formule (expression)  .

 

Le physicien note souvent pour simplifier :  ,  en utilisant la même lettre pour noter la grandeur physique    (mesurable directement) et la quantité    obtenue en mesurant    et en calculant l’expression  .

 

◊ remarque : le physicien traite en fait les variables comme des paramètres.

 

• Ainsi apparaît un risque de confusion : les mêmes parenthèses notent soit la mise en facteur, soit la dépendance “fonctionnelle” des expressions.

 

Avec l’exemple précédent, la notation   représente le plus souvent le produit :    (où le “point” de multiplication lève l'ambiguïté) et non pas l'expression :   .

 

• En outre apparaît un risque de confusion si  dépend d’une troisième grandeur physique  :   .

 

Par exemple, on peut considérer que le point  précédent a une abscisse    variant en fonction du temps  .

 

Le physicien note alors généralement :    en donnant priorité à la grandeur physique : il utilise la même lettre  pour noter  et  car il représente ainsi une même grandeur physique (exprimée en fonction de  ou de ).

 

Le mathématicien par contre, qui donne priorité à la relation formelle, notera forcément de façon différente la  fonction    (qui s’applique a priori à  )  et la fonction composée    qui s’applique à  .

 

Ainsi pour l’exemple précédent, là où un physicien noterait :

            et  

il notera en général :

          .

 

Or cette notation n’est pas celle du mathématicien qui, s’il gardait la même notation, considérerait que :

         pour    alors    (même fonction) ;

raison pour laquelle il note différemment :

           et    (loi de composition des fonctions).

 

◊ remarque : pour le physicien, ceci peut d'ailleurs causer une autre ambiguïté, car    pourrait représenter la grandeur  réexprimée en fonction de la quantité   ,  c'est à dire :  ,  d'où l'importante nécessité des points de multiplication.

 

• Il faut donc être attentif aux “abus” de notation : les mathématiques utilisent des notations souvent plus compliquées, en ce sens qu'elles sont plus abstraites, mais cela est nécessaire pour étudier avec rigueur les notions qui nécessitent des raisonnements précis ; les démonstrations moins délicates sont souvent facilitées par des notations simplifiées… mais seulement si on en comprend en permanence le contexte.

 

 exercice n° I.

 

 

2. Fonctions de plusieurs variables

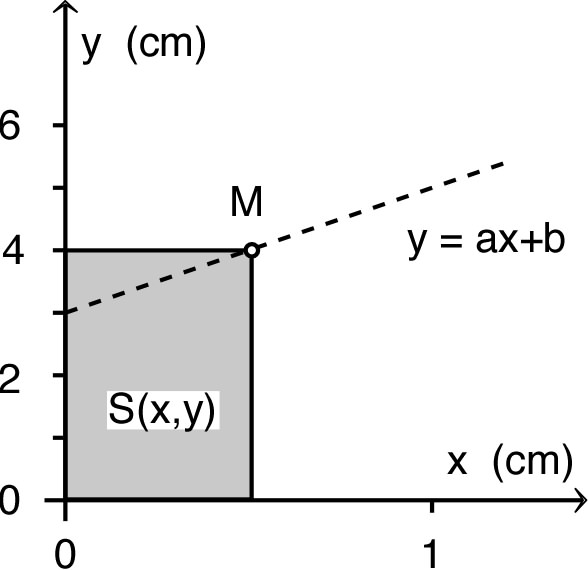
• Dans certains cas, on utilise des expression dans lesquelles interviennent plusieurs grandeurs.

 

Pour un point    dans un plan, on peut calculer la surface délimitée par les axes et le point  :   .

 

• Dans certains cas, on utilise des expression dans lesquelles interviennent plusieurs grandeurs non indépendantes.

 

Pour un point    dans un plan, on peut être amené à considérer le cas où  est contraint à se déplacer sur la droite d’équation    .

 

Il est évident que les deux “variables” ne sont pas indépendantes puisque si  est fixé alors  est imposé et ne peut pas “varier”.

 

Cela n’interdit pas d’utiliser l’expression    dans les calculs, mais il faut alors savoir qu’il n’y a qu’une variable indépendante.

 

Ainsi, si on considère (arbitrairement) que  est la variable indépendante, on peut être amené à noter  comme :    (sorte de fonction composée).