A.M. III - INCERTITUDES DE MESURE

1. Types d’incertitudes

• L’incertitude sur une mesure x peut être exprimée par :
        ◊ l’incertitude absolue  $Δx$  (dont l’unité est compatible avec $x$) ;
        ◊ l’incertitude relative  $\frac{Δx}{|x|}$   (proportion, sans unité).

• L’incertitude de mesure peut être :
        ◊ systématique : pour une série de mesures avec un même appareil déréglé, toutes les mesures sont décalées de façon analogue ;
        ◊ aléatoire : pour une série de mesures d’une même quantité avec des appareils différents, déréglés de façon aléatoire, alors la série des résultats a des “fluctuations” aléatoires autour d’une valeur moyenne non décalée.

• Les incertitudes systématiques (parfois nommées “erreurs”) ne peuvent être réduites qu’en comprenant leur origine et en les corrigeant (par modification des appareils ou par calcul).

Les incertitudes aléatoires peuvent être réduites par des méthodes statistiques : en calculant la moyenne sur un grand nombre de mesures.

2. Répartition statistique

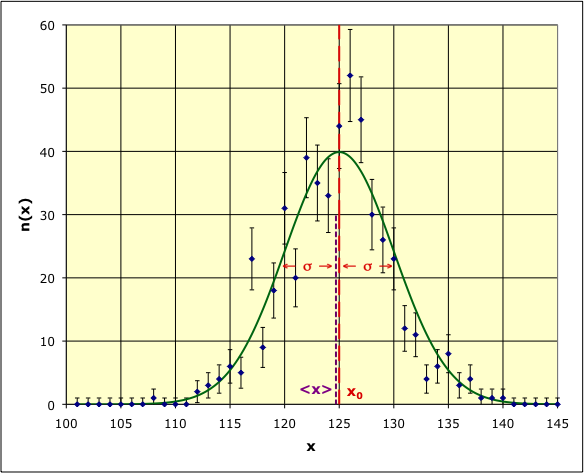
• Pour une série de  $N=500$  mesures d’une même longueur  $x_0=125 \:\mathrm{mm}$  à l’aide de $N$ règles graduées de précision médiocre ($4 \:$), on trace l’histogramme du nombre  $n\left(x\right)$  de fois où la mesure a donné le résultat  $x$.

• Pour une grandeur $x_0$ dont la mesure n’a que des incertitudes aléatoires, la probabilité de trouver une valeur $x$ en mesurant $x_0$ suit souvent la loi de Gauss :  $p(x)=p_0 \:\exp⁡\left(-\frac{\left(x-x_0\right)^2}{2 \:σ^2}\right)$  où la constante  $p_0=\frac{1}{σ \:\sqrt{2π}}$  est telle que  $∫p\left(x\right) \:dx=1$ ,  ce qui correspond à :  $∑n\left(x\right) =N$ .

On obtient une répartition “en cloche”, centrée en une valeur proche de $x_0$ .

La “demi-largeur à mi-hauteur” est de l'ordre de “l’écart-type” $σ$ et correspondant à l’ordre de grandeur de la précision des mesures.

◊ remarque : une incertitude  $Δn≈\sqrt{n+1}$  est superposée à chaque point de l’histogramme pour visualiser l’effet des fluctuations statistiques ; on voit ainsi que la “courbe de Gauss” est comparable à l’histogramme.

• Pour $N$ assez grand  ($N=500$  est très grand pour l’étude d’une longueur), la valeur moyenne :  $\left〈x\right〉=\frac{1}{N} \:∑_{mes} x_i = \frac{1}{N} ∑_{hist}\left(n\left(x\right).x\right) =124,7±0,3 \:\mathrm{mm}$   est une bonne approximation de $x_0$  (l’écart constaté est compatible avec l’incertitude).

• Les calculatrices permettent généralement le calcul de l'écart type (ou de la “variance” :   $\frac{N}{N-1} \left〈\left(x-\left〈x\right〉\right)^2 \right〉≈σ^2$ ; on obtient ainsi :  $σ=4,6 \:\mathrm{mm}$ .

L’incertitude statistique sur la moyenne est alors estimée par :  $Δ\left〈x\right〉≈\frac{σ}{\sqrt{N}}$ .

☞ remarque : l’incertitude ne tend pas vers zéro pour un nombre infini de mesures, car il subsiste généralement des incertitudes systématiques.

• L’incertitude statistique n'est pas une limite infranchissable mais simplement “assez probable” ; ainsi pour une loi de répartition gaussienne :
        ◊ probabilité $≈68 \:$  d’obtenir un écart  $\left|x-x_0\right|<σ$  ;
        ◊ probabilité $≈95 \:$  d’avoir   $\left|x-x_0\right|<2 \:σ$  ;
        ◊ probabilité $≈99,9 \:$  de trouver   $\left|x-x_0\right|<3 \:σ$ ...

◊ remarque : ceci suppose que l'écart type est connu par étude statistique d'au moins vingt mesures ; s'il est seulement estimé d'après de petits échantillons, la répartition suit plutôt la loi de Student.

◊ remarque : si pour des raisons de marges de sécurité, on utilise une incertitude à  $2 \:σ$,  il faut bien l'indiquer pour “propager” correctement son effet sur les calculs utilisant la mesure concernée.

3. Estimations des incertitudes par les fabricants d'appareils de mesure

• Les notices des instruments de mesure doivent normalement indiquer une estimation des incertitudes de mesures (d'après des statistiques effectuées par le fabricant).

Elles sont généralement présentées sous la forme d'un pourcentage plus une constante. Par exemple :  “$0,5 \:$”  signifie qu'une mesure de tension  $U=0,1530 \:\mathrm{V}$  correspond à  $ΔU=\frac{0,5}{100}\: 0,1530 \:\mathrm{V}+0,0002 \:\mathrm{V}=0,0010 \:\mathrm{V}$ .

4. “Propagation” des incertitudes

• Dans le cas d’une grandeur définie par  $f=f\left(x, y\right)$,  l’incertitude $Δf$ peut être estimée par :  $∆f=\left|\frac{∂f}{∂x}\right|\:∆x+\left|\frac{∂f}{∂y}\right|\:∆y$  ;  toutefois, cette façon de calculer est parfois trop pessimiste (incertitude surestimée).

• Si les incertitudes sont essentiellement aléatoires, elles sont estimées par :  $∆f=\sqrt{\left(\frac{∂f}{∂x} ∆x\right)^2+\left(\frac{∂f}{∂y} ∆y\right)^2+2 \frac{∂f}{∂x} \frac{∂f}{∂y} \:\mathrm{cov}\left(x, y\right)}$  afin de prendre en compte les corrélations éventuelles entre $x$ et $y$.

Un estimateur de la covariance est  $\frac{N}{N-1} \left〈\left(x-\left〈x\right〉\right)\left(y-\left〈y\right〉\right)\right〉$  ;  le coefficient de corrélation est tel que  $\mathrm{cov}\left(x, y\right)=\mathrm{cor}\left(x, y\right) \:∆x \:∆y$ .

Quand on ignore s'il y a des corrélations, on peut faire comme s'il n'y en avait pas, mais cela conduit dans quelques cas à des résultats déraisonnables.

• Ainsi par exemple pour un produit  $f=x \:y$  de deux variables indépendantes,  on combine les incertitudes relatives :  $\frac{∆f}{\left|f\right|} =\sqrt{\left(\frac{∆x}{\left|x\right|}\right)^2+\left(\frac{∆y}{\left|y\right|} \right)^2}$.

Par contre pour  $y=x$  ;  $\mathrm{cor}\left(x, y\right)=100 \:$  ;  la relation simplifiée donne :  $\frac{∆f}{\left|f\right|} =\sqrt{2} \:\frac{∆x}{\left|x\right|}$   alors que le résultat corrélé est  $\frac{∆f}{\left|f\right|} =2 \:\frac{∆x}{\left|x\right|}$   (ce qui correspond d'ailleurs dans ce cas à l'approximation pessimiste).

  exercices n° I, II et III.

5. Estimations empiriques des incertitudes

• Lors de l'exploitation des données expérimentales, on est souvent amené à ajuster un modèle théorique pour représenter un ensemble de mesures. Il est alors généralement plus simple, quand c'est possible, de se ramener à des notations telles que le modèle soit affine.

Bien que des méthodes statistiques rigoureuses existent pour estimer les incertitudes sur les coefficients du modèle à partir de l'ensemble des données, une estimation empirique rapide est très souvent suffisante à ce niveau.

• Ainsi, pour une série de mesures représentées par une droite, on commence par vérifier que cette représentation est acceptable (compte tenu des incertitudes sur les points) :

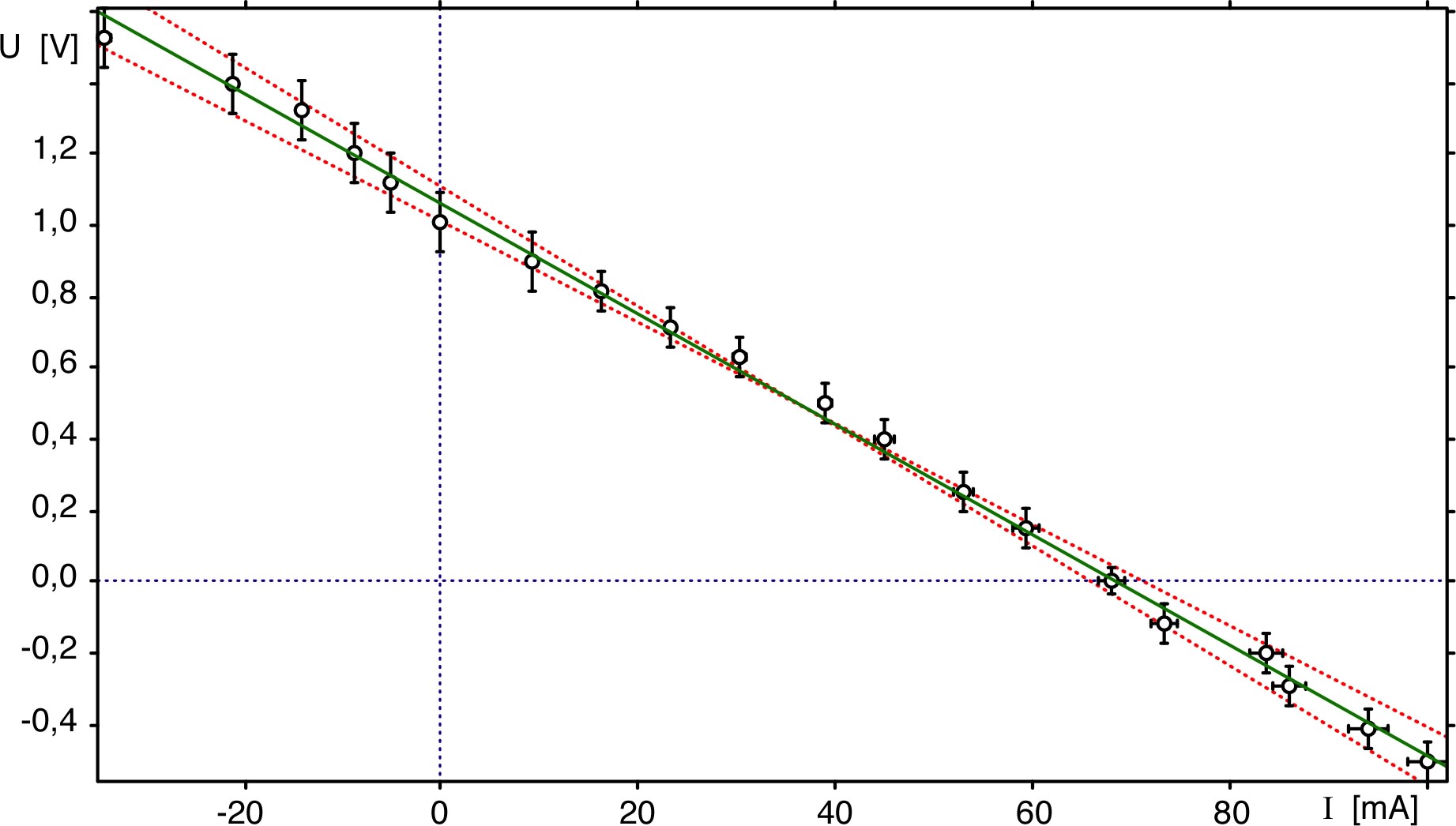
L'incertitude sur la pente  ($-R=-15,49 \:\mathrm{Ω}$)  peut être estimée d'après les incertitudes sur les points, divisées par le facteur statistique lié au nombre de points :  $∆R≈\frac{1}{\sqrt{N-1}} \frac{\left(∆U\left(I_{min}\right)+R \:∆I\left(I_{min}\right)\right)+\left(∆U\left(I_{max}\right)+R \:∆I\left(I_{max}\right)\right)}{I_{max}-I_{min}}≈0,31 \:\mathrm{Ω}$ .

◊ remarque : un logiciel spécialisé calcule plus précisément  $∆R≈0,40 \:\mathrm{Ω}$ .

◊ remarque : si on ajuste le modèle  $U\left(I\right)=E-R \:I$ ,  on constate ici la corrélation positive entre les paramètres $E$ et $R$ : pour que la droite passe “au mieux” par l'ensemble des points, une surestimation de $R$ est associée à une surestimation de $E$ (et inversement).

◊ remarque : si ce type de démarche est appliquée de façon raisonnée, on peut vérifier que l'ajustement du modèle  $I\left(U\right)=\frac{E-U}{R}$  donne le même résultat pour les paramètres $E$ et $R$.

• Il existe des circonstances où les fluctuations de part et d'autre du modèle ne sont que très médiocrement compatibles avec l'estimation des incertitudes.

Si, après vérification de l'absence de biais évident, on juge que le modèle est tout de même acceptable mais que les incertitudes ont été sous-estimées, on peut proposer de les multiplier par un “facteur d'échelle” tel que la compatibilité soit plausible.

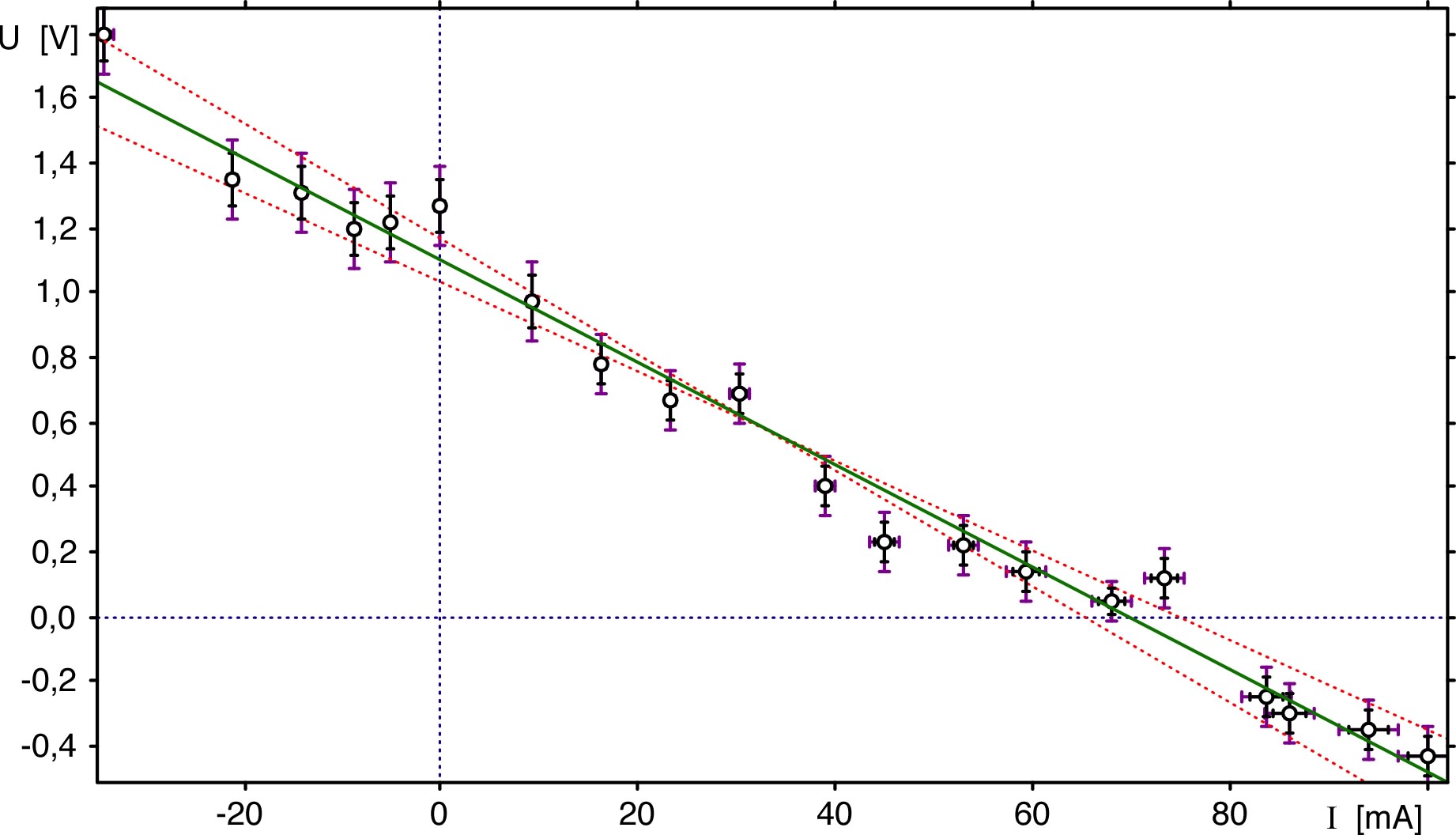
Pour cet exemple, un facteur d'échelle de l'ordre de $1,5$ semble raisonnable ; on obtient ainsi  $R≈15,79±0,48 \:\mathrm{Ω}$.